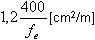Cálculos de paredes de CA de acordo com a NF EN 1992-1-1/NA:2007 (NF P 18-711-1)

As paredes de CA são calculadas de acordo com os princípios indicados em:

• NF EN 1992-1-1/NA:2007 (NF P 18-711-1)
• “Recommandations professionnelles pour l'application de la norme NF EN 1992-1-1 (NF P 18-711-1)”
• EN 1992-1-1/AC:2008

MÉTODO DE CÁLCULO

O projeto da parede é baseado na suposição de que a parede funciona em seu plano como uma seção de CA. A distribuição parabólica linear de tensões de compressão na seção é adotada aqui.

Os cálculos são executados para uma parede sem armadura e, se necessário, para uma com armadura. O processo de projeto está focado na seção inferior da parede.

O algoritmo de cálculo é como segue.

• Para redução de carga, as cargas lineares são reduzidas para o sistema N – M – V.
• Para os cálculos da capacidade de carga de uma parede sem armadura, consulte as descrições de algoritmos de cálculos de parede.
• Se a capacidade de carga de uma parede sem armadura for menor do que o impacto devido às forças reduzidas verticais N, a distribuição uniforme da armadura será considerada.
• Com base na armadura distribuída (a maior das combinações sísmicas e não sísmicas individuais é adotada), a capacidade de carga de uma parede reforçada é calculada (separadamente para estruturas sísmicas e não sísmicas).
• Se a tensão média de compressão na parede ou a tensão média na abraçadeira de compressão exceder a tensão permitida no concreto, os cálculos serão interrompidos. As dimensões da seção da parede devem ser aumentadas.
• São executados cálculos de compressão com flexão, assumindo a resistência da seção da resistência do concreto ou do concreto com armadura distribuída, levando em conta a flambagem da parede (o coeficiente a).
• A armadura para compressão com flexão é organizada próxima das arestas da parede (com zonas ocultas). A armadura vertical distribuída é calculada para poder transportar a força N e a possível armadura resultante da verificação de cisalhamento e deslizamento. Ambas são geradas ao longo de toda a seção.

Nota: As aberturas atualmente são desconsideradas nos cálculos por meio do método clássico. A redução da seção não é levada em conta nos cálculos devido à flexão com compressão nem nos cálculos de tensão tangente. Somente a armadura de construção é gerada próxima da abertura (para paredes sísmicas, é o CV da armadura de aresta mínima).

O algoritmo de cálculos de parede (cargas não sísmicas)

As dimensões básicas de paredes são apresentadas no desenho a seguir.

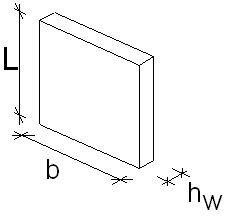
Assume-se que:

• comprimento de parede b ≥ 4 · h_w
• espessura da parede:

  a ≥ 10 cm são paredes internas (e externas), mas, de acordo com EN, todas as paredes sem armadura devem ter ≥ 12 cm, e o usuário pode escolher nas opções de cálculo se é uma parede interna ou externa

  a ≥ 12 cm são paredes externas

• esbeltez λ ≤ 86

As etapas individuais do algoritmo de cálculo para paredes sujeitas a cargas não sísmicas são as seguintes:

• Cálculos de b de acordo com a guia 12.1 (EN 1992-1-1/AC:2008)
• Cálculo do comprimento de flambagem de uma parede l₀, em que l₀= β · l_w
• Cálculo de esbeltez λ, em que λ=l₀/i
• A condição de capacidade de carga da parede é verificada quanto ao nível inferior da parede. A capacidade de carga da seção da parede é verificada quanto a cargas verticais reduzidas e a armadura é distribuída de forma uniforme em toda a seção. Nas etapas subsequentes dos cálculos, a capacidade de carga de uma parede com ou sem armadura é, respectivamente, levada em conta.
• A verificação da capacidade de carga da seção de parede sem armadura é verificada quanto à tensão média de compressão ou à tensão média em abraçadeiras comprimidas

  σ _moy =N/(b · h_w) ≤ σ _ulim

  σ _band,moy =N/(b · h_w) ≤ σ _ulim

  Se a tensão média de compressão na parede ou a tensão média na abraçadeira de compressão exceder a tensão permitida no concreto, os cálculos serão interrompidos. As dimensões da seção da parede devem ser aumentadas.

• Cálculo da capacidade de carga da parede sem armadura N _ulim e da tensão tolerável_ulim

  Φ = min(1-2 · e_tot/h_w; 1.14(1-2 · e_tot/h_w) - 0,02 · l₀/h_w )

  Em que e_tot=e₀+e_i

  N_ulim= b · h_w · f_cd,pl · Φ

  σ _ulim = N_ulim/(b · h_w)

  Se N_umax ≥ N_ulim, a armadura para compressão com flexão será organizada próxima às arestas da parede

• Geração da armadura distribuída na parede

  A relação mínima da armadura vertical deve ser igual a:

  A_s,vmin = 0,002 · A_c

  A relação máxima da armadura vertical deve ser igual a:

  A_s,vmax = 0,04 · A_c

  A distância entre duas barras adjacentes não deve exceder 3 · h_w e 400 mm

  A armadura horizontal cumpre as condições:

  (a armadura é distribuída uniformemente ao longo da altura da parede)

  A_s,hmin = max (25%A_v; 0,001 · A_c)

  A distância entre duas barras adjacentes não deve exceder 400 mm

• Cálculos e geração de armadura de arestas

  Como indicado nas suposições do método, os cálculos dessa armadura estão focados em assegurar que a flexão com compressão possa ser suportada por uma estrutura; ela é gerada em uma 'zona oculta' da largura igual a d'.

• Cálculos de capacidade de cisalhamento de parede sem armadura

  σ _cp = N/(h_w · b)

  t cp = k · V/(h_w · b)

  σ _c,lim = f_cd - 2 · (f_ctd · (f_ctd+f_cd)) ^½

  Se σ _cp ≤ σ _c,lim :

  f_cvd= (f_ctd,pl ² + σ _cp · f_ctd,pl ² ) ^½

  Se σ _cp > σ _c,lim :

  f_cvd= (f_ctd,pl ²+ σ _cp·f_ctd,pl² - 0,25 · ( σ _cp - σ _c,lim )²) ^½

• Verificação de cisalhamento para parede sem armadura

  Se τ _cp <= f_cvd, a armadura de cisalhamento calculada com base nos seguintes critérios deverá ser distribuída uniformemente ao longo do comprimento da parede:

  v_min = 0,35/ γ _c · f_ck ^½

  k = min(1+(200/b) ^½ ); 2)

  C_Rd,c =0,18/ γ _c

  σ _cp =min(0,2 · f_cd; N/(h_w · b))

  V_Rd,c = max((C_Rd,c · k · (100 · ρl · f_ck) ^(1/3)+k₁ · σ_cp )*h_w*d; (v_min+ k₁ · σ_cp ) · h_w · d) ^(1/3))

• Verificação de cisalhamento para parede com armadura

  As cargas ULS verticais devem atender ao seguinte critério:

  V<=V_Rd,c

• Geração de armaduras de construção e antiencolhimento.

  Armadura de antiencolhimento:

  = vertical

  

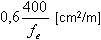
  = horizontal