Os solvers iterativos são usados em equações quando os métodos de reordenação para solvers diretos não são eficientes e a matriz de rigidez K está suficientemente bem condicionada.
Generalidades
Os solvers iterativos são recomendados para problemas em larga escala bem condicionados (15.000 – 1.000.000 equações), tarefas estáticas lineares e problemas de valor próprio (análise modal ou de flambagem).
Os métodos diretos tradicionais, ou seja, os métodos Frontal, Linha do horizonte e Esparso, são demorados e exigem grande quantidade de espaço em disco para armazenar uma matriz fatorada.
Os solvers iterativos, por outro lado, reduzem consideravelmente o tempo de cálculo e os requisitos de armazenamento em disco. No entanto, eles têm algumas desvantagens:
- Apresentam convergência lenta diante de problemas mal condicionados.
- Cada caso de carga é calculado de forma iterativa desde o início. Os casos de carga devem ser definidos o mínimo possível.
Os solvers iterativos são eficientes para a análise de estruturas que contenham FE sólido. Eles também são úteis durante análises estáticas lineares (por exemplo, para procurar parâmetros de projeto ideais), quando é possível obter soluções aproximadas para alguns casos de carga.
O controle elemento a elemento da exatidão de dados da regularização Vinget constitui uma aplicação adicional dos solvers iterativos que permite detectar dificuldades, encontrando erros no modelo FE.
O método de gradiente pré-condicionado (PCG) inclui vários tipos de pré-condicionamento.
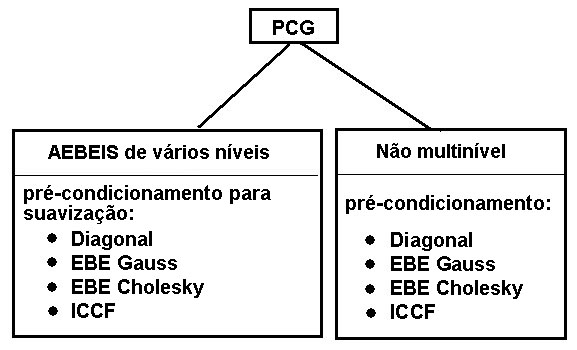
- AEBEIS: solver iterativo de agregação elemento a elemento 1,2.
- EBE: elemento a elemento.
- ICCF: abordagem de fatoração de Cholesky incompleta.
Solvers iterativos elemento a elemento (PCGEBE) e multinível (AEBEIS)
O solver elemento a elemento (PCGEBE) é usado para todos os tipos de elementos finitos e não é limitado pelo tamanho do problema. No entanto, é sensível ao mau condicionamento da matriz de rigidez K, o que implica uma possível convergência lenta.
O solver iterativo multinível (AEBEIS) é um solver iterativo elemento a elemento, de agregação e vários níveis, que combina as vantagens dos métodos iterativos rápidos com a técnica EBE de baixo custo. Permite a aceleração das operações básicas por meio do método de baixo custo no que diz respeito aos requisitos de memória. Métodos de agregação como esses permitem a análise de sólidos e cascas (tal como os métodos de várias grades), assim como barras e estruturas de combinação de barras, cascas e sólidos.
O solver AEBEIS normalmente fornece convergência mais rápida em comparação com métodos que não são do tipo multinível. Garante uma convergência estável para problemas mal condicionados, mas é menos seguro. Em casos raros, o pré-condicionamento é bloqueado, enquanto a convergência ainda é lenta. Esse solver foi implementado em combinação com o solver de agregação com base na técnica EBE.
O solver AEBEIS permite a aplicação de elementos de barra 2D e 3D, elementos de casca (elementos de 3, 4, 6 e 8 nós) e elementos sólidos. Também permite elementos adicionais de componentes de estrutura, como apoios elásticos, deslocamentos, liberações e vínculos rígidos. Não existem restrições relativas aos tipos de elementos ou de estruturas para um método não multinível.
Os seguintes tipos de pré-condicionamento estão disponíveis nos métodos AEBEIS e não multinível.
- Diagonal – pré-condicionamento de Jacobi (aplica-se apenas em problemas bem condicionados).
- EBE Gauss – pré-condicionamento EBE Gauss-Seidel-Cholesky modificado 12.
- EBE Cholesky – pré-condicionamento EBE Cholesky 34.
- ICCF – abordagem de fatoração de Cholesky incompleta 56.
A abordagem ICCF é mais rápida do que outros métodos (Diagonal, EBE Gauss, EBE Cholesky) e usa aproximadamente o mesmo número de iterações para obter convergência, tal como os métodos EBE Gauss ou EBE Cholesky. Não usa as operações de E/S do disco, mas apresenta requisitos superiores de RAM. A abordagem ICCF será preferível se o computador tiver RAM suficiente para a tarefa. Os requisitos de RAM e de disco dos métodos EBE Gauss e EBE Cholesky são mínimos, mas são mais lentos do que a abordagem ICCF.