应用可以设置动画的高度可自定义的多色渐变。
渐变坡度与渐变贴图类似,但是可以指定任何数量的颜色或贴图,并且几乎任何参数都可以设置关键帧。
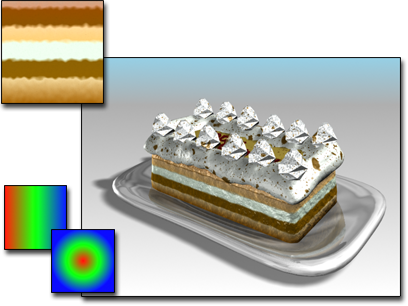
渐变坡度用于蛋糕的层
当用渐变坡度贴图替换现有贴图时,在“替换贴图”对话框中选择“将旧贴图保存为子贴图”,旧贴图将作为纹理而应用到第一个标志。
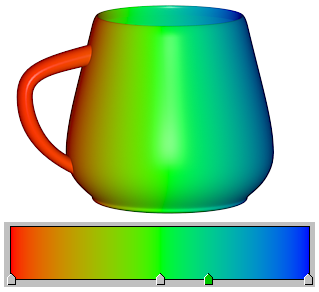
带有颜色渐变的“渐变坡度贴图”材质
界面
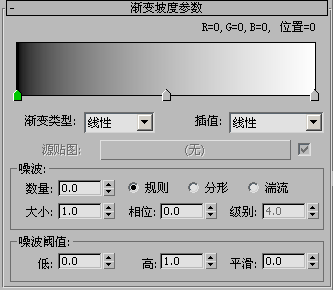
渐变栏显示默认的渐变和插值类型
- [渐变栏]
- 显示正在创建的可编辑渐变表示形式。渐变的效果从左(始点)移到右(终点)。
默认情况下,三个标志沿着红/绿/蓝渐变的底边出现。每个标志控制一种颜色(或贴图)。当前所选的标志是绿色,其 RGB 值和在渐变中的位置(范围为 0 到 100)出现在渐变栏的上方。每个渐变可以有任意数目的标志。
渐变栏有以下功能:
- 单击沿着底边的任何位置,可以创建附加的标志。
- 拖动任何一个标志,可以在渐变内调整它的颜色(或贴图)的位置。不可以移动起始标志和结束标志(0 处的 标志 #1 和 100 处的 标志 #2)。但其他标志可以占用这些位置,而且仍然可以移动。
- 对于一个给定的位置,可以有多个标志占用。如果在同一个位置上有两个标志,那么在两种颜色之间会出现轻微边缘。如果同一个位置上有三个或更多的标志,边缘就为实线。
- 渐变栏的右键单击选项
- 在渐变栏中右键单击以显示带有以下选项的菜单:
- 重置将渐变栏重置为默认值。
- 加载渐变将现有的渐变 (DGR) 文件加载到渐变栏中。
- 保存渐变将当前的渐变栏保存为 DGR 文件。
- 复制复制渐变。
- 粘贴将复制的渐变粘贴到当前的渐变中。
- 加载 UV 贴图加载 UV 贴图以控制当前的渐变。
加载 UV 贴图将关闭标志模式。
- 加载位图加载位图以控制当前的渐变。
加载位图将关闭标志模式。
- 标志模式切换标志的显示。
启用标志将禁用可能已加载的贴图。
- 标志的右键单击选项
-
右键单击任一标志以显示带有以下选项的菜单:
- 编辑属性选择此选项可显示“标志属性”对话框。
- 复制复制当前标志值。
- 粘贴将标志值粘贴到当前标志中。
注: 您可以粘贴到当前贴图以外的“渐变坡度”中。
- 删除删除标志。
- “渐变类型”下拉列表
-
选择渐变的类型。以下“渐变”类型可用。这些类型影响整个渐变。
- 4 角点颜色的不对称线性变换。
- 长方体长方体。
- 对角线颜色的线性对角线变换。
- 照明基于灯光的强度值。无灯光表示最左边;最亮灯光表示最右边。
- 线性颜色的平滑线性变换。
- 贴图用于指定贴图以用作渐变。启用“源贴图”控件以便指定该贴图,并启用和禁用它。
- 法线基于从摄影机到对象的向量和示例点曲面法线向量之间的角度。渐变最左端的标志为 0 度;而最右端的标志为 90 度。
- 往复在中部进行重复的对角线扫描。
- 径向颜色的径向变换。
- 螺旋颜色的平滑圆形变换。
- 扫描颜色的线性扫描变换。
- 格子格子。
- “插值”下拉列表
-
选择插值的类型。以下“插值”类型可用。这些类型影响整个渐变。
注: 渐变按照从左到右的顺序排列。“下一个”标志在当前标志的右方;“上一个”标志在当前标志的左方。- 自定义为每个标志设置各自的插值类型。右键单击标志可显示“标志属性”对话框并设置插值。
- 缓入与当前标志相比,为下一个标志指定的权重更大。
- 缓入缓出与下一个标志相比,为当前标志指定的权重更大。
- 缓出与下一个标志相比,为上一个标志指定的权重更大。
- 线性(默认设置。)从一个标志到另一个标志的常量。
- 匀值无插值。变换是清晰的线条。
- 源贴图
- 单击可将贴图指定给贴图渐变。该复选框可启用或禁用贴图。
仅当选择渐变类型后,“源贴图”控件才可用。
“噪波”组
- 数量
- 当为非零时,将基于渐变坡度颜色(还有贴图,如果出现的话)的交互,而将随机噪波效果应用于渐变。该数值越大,效果越明显。范围从 0 到 1。
- 规则生成普通噪波。基本上与禁用级别的分形噪波相同(因为“规则”不是一个分形函数)。
- 分形使用分形算法生成噪波。“层级”选项设置分形噪波的迭代数。
- 湍流生成应用绝对值函数来制作故障线条的分形噪波。注意,要查看湍流效果,噪波量必须要大于 0。
- 大小
- 设置噪波功能的比例。此值越小,噪波碎片也就越小。
- 相位
- 控制噪波函数的动画速度。对噪波使用 3D 噪波函数;第一个和第二个参数是 U 和 V,而第三个参数是相位。
- 级别
- 设置湍流(作为一个连续函数)的分形迭代次数。
“噪波阈值”组
如果噪波值高于“低”阈值而低于“高”阈值,动态范围会拉伸到填满 0 到 1。这样,阈值过渡时的中断会更小,潜在的锯齿也会变得更少。
- 高
- 设置高阈值。
- 低
- 设置低阈值。
- 平滑
- 用以生成从阈值到噪波值较为平滑的变换。当“平滑”为 0 时,没有应用平滑。当“平滑”为 1 时,应用了最大数量的平滑。