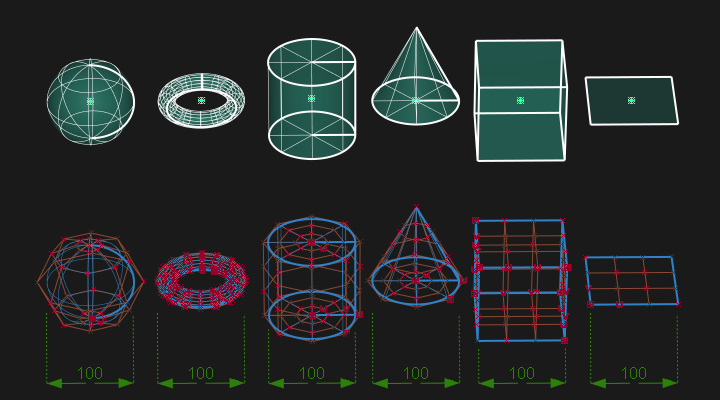
基本体 (NURBS)
![]()
可以创建以下 NURBS 基本体:
 球体
球体  圆环体
圆环体  圆柱体
圆柱体  圆锥体
圆锥体  立方体
立方体  平面
平面
- 通过在场景中单击或在提示行中输入坐标位置来放置基本体。
- 基本体以默认大小 100 个单位创建。使用操纵器、变换工具或信息窗口来更改这些大小。
- 基本体的轴心点默认为几何体的中心(轴心位于底面中心的圆锥体除外)。
- 可以通过显示 CV 以及使用“Pick”和“Transform”工具来塑形基本体。
- 立方体是包含 6 个曲面的组
- 如果在选项中选择了端封口,则“Cylinder”和“Cone”将成为一个组。
- 选择 360 度扫掠后,球体、圆柱体、圆锥体和圆环体将成为周期性曲面。
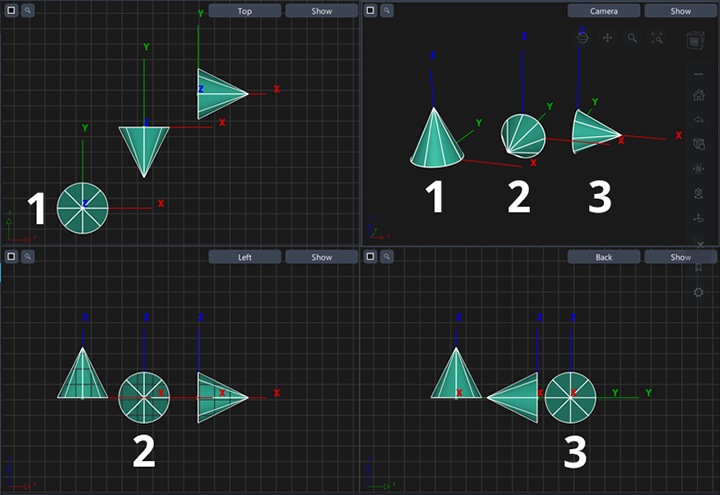
用于放置的视图窗口将影响基本体的方向和局部坐标轴,如下图所示:
- 显示放置在“Perspective”视图和“Top”视图窗口中的基本体圆锥体,或通过在提示行中键入坐标来显示基本体圆锥体。
- 显示放置在“Left”视图或“Right”视图窗口中的基本体圆锥体。
- 显示放置在“Front”或“Rear”视图窗口中的基本体圆锥体。
从“Surfaces”工具箱访问 NURBS 基本体工具:

使用操纵器
- 拖动箭头以沿着某个坐标轴移动对象。
- 单击某个箭头,然后使用鼠标键拖动操纵器中心处的星形以自由地移动对象。
- 拖动立方体以沿着某个坐标轴缩放对象。
- 单击某个立方体,然后拖动操纵器中心处的立方体以均匀缩放对象。
- 拖动球体或圆弧以绕某个坐标轴旋转对象。
- 单击某个球体,然后使用鼠标键拖动操纵器中心处的球体以自由地旋转对象。
另请参见
“Sphere Primitive”选项
Sphere Type
- Surface - 基于单个 NURBS 曲面创建球体。
 Self Inflated Cube - 从缝合为一个壳的六个四次单跨距 NURBS 曲面创建球体。
Self Inflated Cube - 从缝合为一个壳的六个四次单跨距 NURBS 曲面创建球体。- Shell Tennis Ball - 通过两个缝合为一个类似于网球的壳的互锁曲面创建球体。
- Shell No-Pole - 通过八个缝合为一个壳的曲面创建球体。
Object Degree
用于创建球体的曲面的阶数。选择 1(线性)到 7。
Sweep
围绕径向基本体的中心旋转的度数。
例如,如果在球体工具中输入 180 度,Alias 将会创建一个半球体。
Sections
曲面上的细分(跨距)数目。
默认值为 8。要创建一个可用的基本体形状,通常需要至少 4 个细分。通常不需要使用 20 个以上的细分。
“Torus Primitive”选项
Sweep
围绕径向基本体的中心旋转的度数。
例如,如果在圆环工具中输入 90 度,Alias 将会创建 1/4 个圆环体。
Size
“Size”可以是“Absolute”,也可以是“Relative”,它决定下列哪个参数是可设置的。
Major radius
环状体中心与管状体中心之间的距离。只有“Size”设置为“Absolute”时,此选项才可用。
Minor radius
管状体的半径。只有“Size”设置为“Absolute”时,此选项才可用。
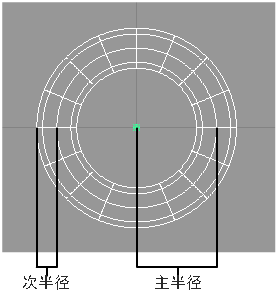
Ring Thickness
环状体的直径(相对于整个圆环体的直径而言)。只有“Size”设置为“Relative”时,此选项才可用。
环状体的厚度越接近 0.5,圆环体的孔就越小。当环状体厚度为 0.5 时,圆环体将不再有孔。请参见下图。
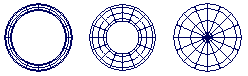
“Cylinder Primitive”选项
Degree
用于创建圆柱体的曲面的阶数。选择 1(线性)到 7。
Sweep
围绕径向基本体的中心旋转的度数。
例如,如果在球体工具中输入 180 度,Alias 将会创建一个半圆柱体。
Spans
沿圆柱体长度的跨距数。
默认值为 8。通常至少需要 4 个跨距,才能创建一个可用的基本体形状。通常不需要使用 20 个以上的跨距。
Caps
创建周期性曲面以闭合圆柱体的末端。选择 0(无封口)、1(仅底部有一个封口)或 2(两端均有封口)。
“Cone Primitive”选项
Degree
用于创建圆锥体对象的曲面的阶数。选择 1(线性)到 7。默认值为 3。
Sweep
围绕径向基本体的中心旋转的度数。
例如,如果输入 180 度,Alias 将创建一个半圆锥体。
Spans
沿圆锥体长度的跨距数。
默认值为 8。通常至少需要 4 个跨距,才能创建一个可用的基本体形状。通常不需要使用 20 个以上的跨距。
Caps
创建周期性曲面以闭合圆锥体的开口端。
“Cube Primitive”选项
Object Degree
用于创建立方体的曲面的阶数。选择 1(线性)或 3(三次)。
“Plane Primitive”选项
Object Degree
用于创建平面的曲面的阶数。选择 1(线性)或 3(三次)。
关于 NURBS 曲面无法完成的任务
由于 NURBS 曲面的内在表示,无法对某些内容进行建模:
与矩形板不等价的拓扑。
球体、圆锥体、圆环体和三角形全部可以通过连接或折叠边来使用矩形板构建。但是,更加复杂的形状(例如星形)不能使用简单的 NURBS 曲面表示。要获取复杂的曲面轮廓,必须使用修剪的曲面或四边形曲面的网络或集合。
孔。
要在曲面上创建孔,应使用修剪的曲面。
不能使用常规的 U 和 V 坐标绘制的曲面。
例如,可以为麦比乌斯带的形状建模,但是曲面将包含缝隙。
关于法线和曲面方向
法线是与曲线或曲面上的每个点垂直的虚构线。

根据右手规则,曲面上 U 等参线和 V 等参线的方向决定曲面法线的方向。此规则如下:如果右手的大拇指指向 U 方向,食指指向 V 方向,则与这两个手指呈直角弯曲的中指指向曲面法线方向。
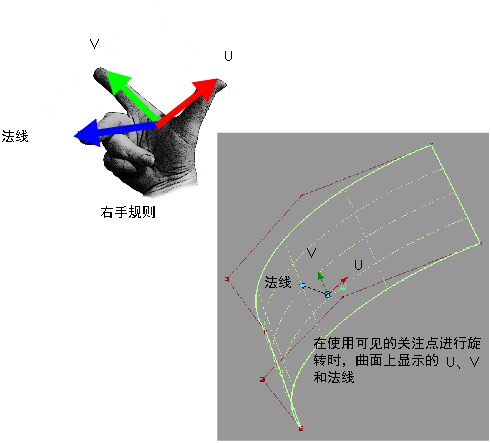
法线还可以间接指示曲线或曲面的形状。因为法线始终与曲线或曲面垂直,如果法线之间相互靠近或彼此远离,则表明存在微小的曲率。
对于建模/评估来说,曲面的方向(朝向的方向)不同于 U 方向和 V 方向(切线)。更改曲面的方向可以保留构建历史,而不会影响纹理贴图。
所有工具(“Ambient Occlusion”、“Draft Evaluation”、“Parting Line”和“Offset”)都使用方向而不是曲面法线来确定曲面面向的方向。在“Surface Edit”>“Orientation”子菜单中提供了三个工具,可用来修改曲面的方向。使用这些工具翻转曲面不会影响曲面的 U 方向和 V 方向。因此,方向可能对应于法线的相同方向(默认情况下)或相反方向。
诊断着色显示的“Multi-Color”模式使用黄色和红色显示可视法线和几何法线的方向。当“Show the Orientation Mode”设置为“Visual”时,黄色表示曲面的背面面向查看者。当设置为“Geometric”时,红色表示几何法线被反转。再次说明一下,此方向独立于 U 方向、V 方向和曲面法线,如下图所示。
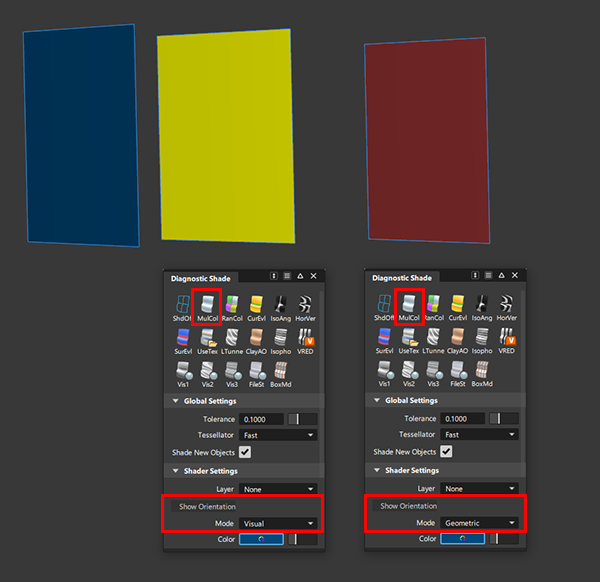
如果需要修改曲面的 U 方向或 V 方向,可以使用单独的工具(“Surface Edit”>“Reverse Surface UV”)来完成,这会影响曲面法线,但不影响曲面的方向。在某些情况下可能必需按上述方式修改方向,例如,反转纹理贴图时。
导出文件时,将转换曲面方向信息(假设该文件格式能以某种方式支持该信息)。
关于壳
壳是一种特殊类型的曲面或曲面集合,可以用于特殊的建模操作,或用于导出到实体建模工具包。
壳是相邻 NURBS 曲面的集合。缝合入壳的每个曲面都必须在某个点上与壳中的另一曲面的边相接。
壳在 DAG 中存储为一个节点。
壳可以是开放的,也可以是闭合的。对于闭合的壳,法线应始终指向外部。对于布尔运算,这是必要的。
壳的主要用途是:
改进向某些 CAD 软件包的数据传输方式。
某些 CAD 软件包处理壳的能力要明显好于处理普通的修剪过的 NURBS 曲面。
准备进行布尔运算。
布尔工具(布尔减集、布尔交集和布尔和集)只适用于壳。通常,只需要将曲面缝合到壳中,应用布尔运算,然后再取消缝合,恢复为曲面。
检查曲面之间的相邻性。
曲面只有处于相邻性公差范围内,才能缝合到壳中。
如果设置的公差正确,通过检查某个曲面组是否将一起缝合到壳中,可以很容易检查是否能够正确地导出或构建该曲面组。
标识缝合的壳中的开放边:
使用 Query Edit 工具
 检查壳中是否有开放边。红色箭头清晰地标记壳中的间隙。
检查壳中是否有开放边。红色箭头清晰地标记壳中的间隙。
壳具有下列局限性:
根据“Shell stitch option”窗口中的选项,缝合的壳可能与原始曲面不完全匹配。
在这种情况下,取消缝合也不会生成与原始曲面完全一样的曲面。
不能编辑壳的 CV。如果需要改变壳曲面的形状,必须取消壳的缝合。
不能使用壳曲面的等参曲线作为其他工具的输入。
不能在“Square”和“Rail Surface”等工具中保持与壳的连续性。
不能在壳上或壳与其他曲面之间创建圆角曲面。
如果缝合某个对象,缩放该对象,然后再取消缝合,则无法再重新缝合该对象。这是因为缩放操作可能会增大曲面之间的间隙,从而导致所有后续缝合操作失败(在当前公差设置内)。在这种情况下,应在首次缝合对象之前缩放对象。
关于有理几何体与非有理几何体
非有理几何体是多项式的和。有理几何体(其数学表示)是多项式和之比。从数学角度而言,有理几何体要复杂得多。因此:
- 可能无法传输给不能处理复杂描述的后续 CAD 软件包。
- 当建模时,操纵速度可能较慢。
下表列出了两种几何体之间的区别。
| 性质 | 优点 | 缺点 |
|---|---|---|
| 非有理几何体 | 变换更加灵活,速度更快。 | 建模更灵活,但因此降低了精度。 |
| 有理几何体 | 精确的几何体(即精确的二次曲线)。 | 许多 CAD 软件包不支持加权 CV。加权 CV 更难操纵,会创建多余节点。显示速度较慢。 |
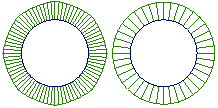
下图显示使用上述两种几何体绘制的两个圆。
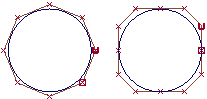
- 左侧的圆是非有理性曲线,其 CV 的权重全部相等。要绘制非有理性曲线,所有权重必须都是 1.0。
- 右侧的圆是有理曲线,对 CV 应用不同的权重,并且具有多余节点。
可以通过两种方式看到它们的区别:
如果对圆进行半径测量,则非有理性圆不是真正的圆(尽管非常接近):它在不同测量位置的半径不同。有理圆是个真正的圆。
将曲线曲率梳连接到圆上。左侧非有理性圆上的曲率会变化。右侧有理圆上的曲率是恒定的。