网格相关性

众所周知，有限元求解与网格相关。当您尝试比较预测结果与实验结果时，请务必记住这一点。FEA 模拟中使用的网格大小对您的求解可能有着很大的影响。

网格大小对失效的影响

结构的极限失效很大程度上由 FEA 模型中发现的峰值应力驱动。由于这些峰值应力可能因网格大小而异，因而您可以根据网格大小预期不同的极限应力。

通常，较大的单元大小会产生较高的预测极限应力。之所以如此是因为较大单元中的积分点更远离应力集中。因此，在发生失效之前，单元能够保留更多的载荷。在较小的单元中，积分点更接近应力集中。因此，它们可能会较早地失效，从而产生较低的预测极限应力。我们可以在下图中看到此效果的样例。

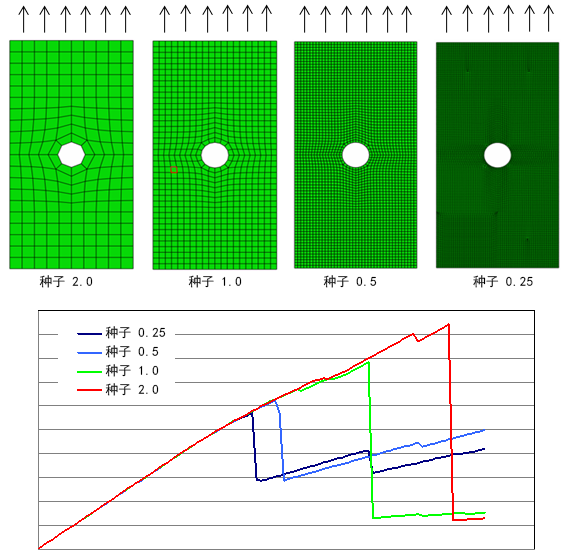
在这里我们看到的是一个空心样本模型，有着四种不同的网格大小。当我们绘制每个模型的载荷-位移响应图时，我们可以看到网格大小的不同将怎样影响预测极限载荷。当使用小网格时，失效会更快速地从孔上的应力集中传播。

网格大小对 Ramberg-Osgood 材料参数的影响

用于定义弹塑性材料模型的 Ramberg-Osgood 材料参数对网格大小也很敏感。如果您尝试手动修改非线性材料的 Ramberg-Osgood 材料参数，应考虑用于校准这些参数的网格大小。进行网格敏感度分析时，建议使用此步骤。另外，请务必对模型使用与校准材料参数时使用的最匹配的网格大小。