非线性弹性纤维

当单向复合材料加载到大型纤维定向轴向应变时，它们倾向于展现非线性弹性。

非线性弹性（复合材料 E11 的主要影响因素）可能是由于纤维 [21] 中微晶的排列引起的。微晶在纵向拉伸上变得更均衡，从而增加了刚度。纤维压缩时情况则相反，由于微晶解取向，从而导致刚度降低。当纤维处于受拉状态时，Helius PFA 使用 Murphey et al[21] 提出的第一顺序模型，以通过修改使用割线模量来修改纤维的模量（方程 28）。

其中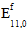， 是原始纤维模量、 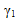是非线性参数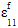， 是假定等于复合轴向应变的纤维轴向应变。混合规则用于基于更新的纤维模量 (Eq. 29)。

其中 φi 是纤维 (i=f) 和基体 (i=m) 的体积因子。 所有其他纤维和复合弹性常量将保留其原始值。

有两个选项可用于修改模型软化行为压缩方面的纤维模量。可以将 Eq. 28 与其他非线性参数 (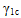) 一起使用。另外，复合模量抑制因子 ηc 可用于模拟软化行为，如 Eq. 30。

其中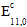， 是原始的复合模量。所有其他纤维和复合弹性常量将保留其原始值。

Eq. 31 是对压缩非线性参数 (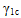) 值的限制，这将阻止模量在失效出现前归零。

其中，C1 是纵向压缩强度的绝对值。

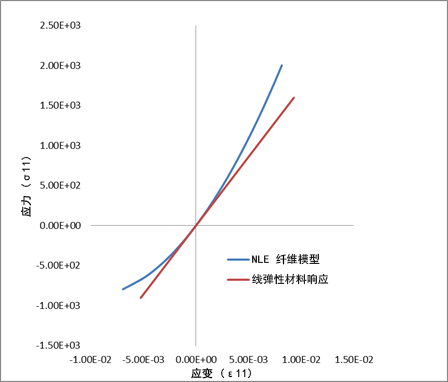
下图使用不同的非线性参数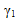（ 和 ηc）来比较纯轴向载荷下材料的复合级应力-应变行为。黑色虚线表示非线性弹性纤维模型处于未启用状态时使用的线性弹性响应。

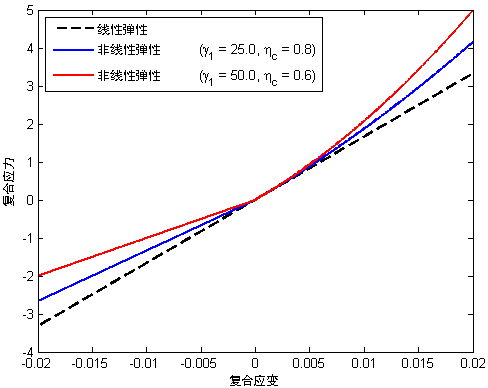
下图显示了将 Eq. 28 中指定的模型用于压缩和拉伸时纵向应力-应变响应之间的比较。