确定用于预测连接断开和连接修复速率的平均基体应力。

根据复合应力状态或应力记录，根据 Eq. 40 预测连接断开率，根据 Eq. 41 预测连接修复率。在此过程中，一个明显的难题是确定如何表示作为可与描述 KTF 的方程一起使用的有效标量应力的基体应力张量。多个研究人员已指明，用于预测疲劳寿命的相应参数为通过相同载荷条件 [23, 44-45] 下的静态强度规格化的疲劳强度。这通常称为强度-寿命等级假设。因此，我们将静态失效准则的函数形式用于确定有效疲劳应力。

单向复合材料

单向复合材料显示层平面中疲劳失效的两个单独的模式（或过程）：离轴和同轴。每个过程必须拥有自己的激活能量和激活体积，因为两种开裂的微型开裂累积的物理量也不同。此外，有效的应力定义也不同。在本节中，我们定义离轴和同轴载荷的有效基体应力。

离轴

在考虑失效准则的形式时，考虑在实验中观察到的离轴失效模式会很有用。疲劳失效通常通过与单向复合材料的纤维 [24, 46] 平行的开裂而发生，这已被广泛报告。因此，需要垂直于纤维的拉伸力在这些平面上的疲劳和剪切应力中起到非常重要的作用。通过将纤维的轴方向设置为 1 个方向，我们提出现场基体失效准则，该准则的形式是使用成形的 MCT 计算的基体应力张量的横向各向同性不变量。

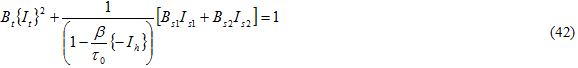
其中

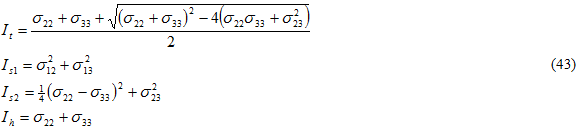
和 {} 表示 Macaulay 括号，以便在包括的数量为负值时该值为零。Bi 的值由三项复合静态失效测试确定：横向拉伸、横向压缩和平面内剪切。每项测试均涉及到基体成分的失效。将 Eq. 42 除以 Bs1 形成有效应力 σ eff

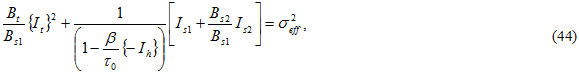
其中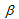， 是压力加固系数，而 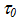则是没有压力加固的基体剪切强度。在当前版本中，所有计算均使用 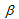= 0\。使用 Eq. 44 的平方根并根据 Eq. 40 和 41 提供计算连接断开率的有效应力。

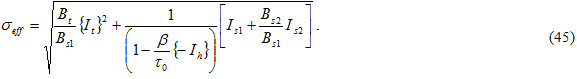
同轴

同轴载荷失效源于在纤维/基体界面获取的基体裂纹。这些裂纹主要由轴方向的正常应力驱动。因此，对于同轴失效 (θ = 0°) 的情况，有效应力如下定义