热激活过程

查看热激活过程如何影响 KTF。

温度大于绝对零度的所有原子和分子都按照与普朗克定律所指定的 n 0 成比例的频率振荡。

其中，h 是普朗克常数 (h = 6.626068 × 10-34­ J-s/K-atom)，kT 是波耳兹曼常数 k (k = 1.3806504 × 10-23­ J/K-atom) 和绝对温度 T 的乘积所表示的热能。但是由于与每次振荡关联的热能实际上不是单个数，而是一个分布，因此始终存在以下可能性：任何给定的振荡有足够的能量来克服能量障碍 U，并从一种平衡状态移到另一种平衡状态。任何给定振荡发生此情况的可能性由熟悉的指数形式 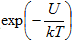指定。因此，粘合断裂率 K b 可简写为

出于断裂和疲劳的目的，一种平衡状态是未断裂状态，而另一种是断裂状态。下面的左图大略显示了该过程。因此，可以为粘合愈合写出相似的方程，如下所示

现在请考虑已应用的应力对方程 (38) 中所述的粘合断裂率和方程 (39) 中所述的粘合愈合率的影响。在此上下文中，从每单位体积的能量（而不是每单位面积的力）的角度来思考应力更有帮助。因此，如果应力用于促进粘合断裂过程，它应降低粘合断裂的能量障碍，并增加粘合愈合所需的能量障碍。

此差异取决于材料体积 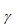、发生此过程的激活体积 1，因此激活能量的减少只是激活体积和应力的产物。下面的右图显示应力如何修改激活能量。修改方程 (38) 以反映已应用的应力所产生的效果。

同样，对于 Eq. 39

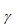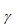注意：粘合愈合和粘合断裂中的 U 值和 不同，因为这两个过程中的激活能量和激活体积在物理上不同。Eq. 40 和 41 是 Helius PFA 用于预测复合疲劳的 KTF 的基线方程。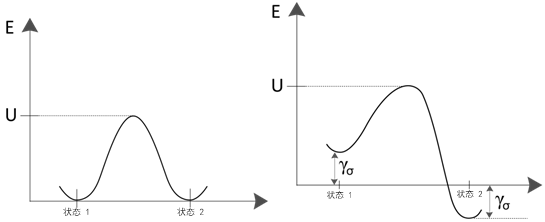

1 对于聚合物断裂的过程，激活体积的精确定义在某种程度上不明确，因为它比原字体积大很多。 因此，它通常仅定义为发生激活过程的体积。