残余应力收缩预测方法(MP 和 DD)
残余应力收缩预测模型的公式化表达基于热粘弹性材料行为假设条件。它考虑材料在模具中受压冷却时产生的应力。在此方法中,我们直接计算每个单元的残余应力分布,而不计算收缩应变。
残余应力分布在与流向平行和垂直的方向上提供每个单元各个厚度上的应力。这种应力分布随后输入应力分析程序以获取零件的偏移形状。此外,如果材料可使用经验性收缩数据,则相对于使用残余应变方法,这种方法可获得精度大为提高的收缩预测,进而获得更精确的材料变形。
方法综述
该模型的公式化表达基于热粘弹性材料行为假设条件。它考虑材料在模具中受压冷却时产生的应力。特别地,该模型还考虑热致应力(产生自材料的冻结和随后的收缩)以及压致应力。后一种应力的产生是对形成冻结层的固化材料施加熔压所致。该模型以理论为基础,优势在于即使材料没有可用的收缩数据,模型也可使用。但如果有收缩数据可用,模型性能可大幅度提升。
收缩和翘曲的预测均基于计算出的热致及压致应力分布。目前开发出的计算过程如下所列。该过程适用于纤维填充材料。对于未添加填充物的材料,过程大致相同,但无需计算机械特性。
对于每个时间步:
流体力学计算:
- 压力 p、流动速率 Q...
- 纤维取向
热传导计算:
- 温度 T
- 冻结层
热力学计算:
- f (p, v, T)=0
更新粘度。
解是否收敛?
- 如果不收敛,从步骤 1 开始重复操作。
- 如果收敛,转至步骤 6。
微机械计算:
热机械特性:
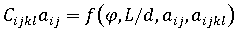
热粘弹性计算:
- 热致和压致应力
如果
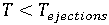 ,则转到下一时间步(从步骤 1 开始重复操作)。
,则转到下一时间步(从步骤 1 开始重复操作)。
没有收缩数据时应用此方法
对于线性热粘弹性,各向异性应力-应变关系的一般形式可写成
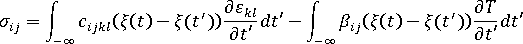
其中:
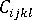 和
和 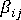 是分别定义材料的机械特性和热特性的张量。
是分别定义材料的机械特性和热特性的张量。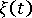 是考虑材料的温度依赖性的伪时间比例,其定义为
是考虑材料的温度依赖性的伪时间比例,其定义为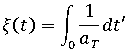
其中,
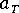 是由 WLF 方程或 Arrhenius 方程(取决于材料和温度范围)表征的时间-温度偏移因子。
是由 WLF 方程或 Arrhenius 方程(取决于材料和温度范围)表征的时间-温度偏移因子。
据发现,热粘弹性模型对材料数据极其敏感,该模型实际上也无法充分利用材料数据。在无法通过实验获得粘弹性数据的情况下,我们利用两种形式的粘性-弾性模型:
- 对于非纤维填充材料,模型是各向同性的,因此机械特性张量
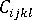 由材料的模量和泊松比(存储在 Autodesk Moldflow 材料数据库中)定义,而用于定义热特性张量
由材料的模量和泊松比(存储在 Autodesk Moldflow 材料数据库中)定义,而用于定义热特性张量 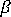 的热膨胀系数则获取自材料的 pvT 数据。
的热膨胀系数则获取自材料的 pvT 数据。 - 对于纤维填充材料,使用复合材料的各向异性机械和热特性定义这些张量,而特性根据获取自“填充+保压”分析的纤维取向分布计算。这种情况下,模型预测纤维取向方向上的横向和纵向应力。
粘性-弾性模型基于以下假设条件:
- 在材料低于转变温度之前,材料中不形成应力。
- 对于 x3 方向垂直于局部中性面的局部单元坐标,剪切应力 =
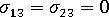 。
。 - 法向应力
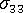 在厚度方向上恒定。
在厚度方向上恒定。 - 只要
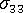 < 0,材料就附着在模具壁上。
< 0,材料就附着在模具壁上。 - 只要材料处于模具中,在任何情况下都规定受约束淬火条件。
- 忽略模具弹性。(在型芯偏移分析中考虑模具型芯的弹性。)
- 顶出零件后,材料表现为弹性实体。
此模型可用于 Autodesk Moldflow 材料数据库中的所有材料,无论它们是否经过收缩鉴定。对于纤维填充材料,模型要求在“工艺设置向导 - 填充+保压设置”对话框中选中用于执行“如果有纤维材料进行纤维取向分析”的选项。
此模型能够预测收缩趋势,但得到的绝对值可能有很大误差。它对设计翘曲减小方案很有用,但相对于使用收缩数据,此时的绝对值精度较低。对于未添加填充物的材料,模型具有各向同性,因为流动分析软件中没有计算分子取向效应或结晶的功能。
有收缩数据时应用此方法
影响上述理论模型预测精度的主要因素有:
- 收缩对转变温度和 pvT 数据的敏感依赖性(无法使用现行测量方法表示出实际注塑成型条件下的行为)。
- 不能确定分子取向,更无法用于未添加填充物的材料,模型无法预测各向异性。
- 缺少针对结晶效应的规定。
- 缺少针对粘弹性计算的松弛幅度数据。
如果 Autodesk Moldflow 鉴定出材料已收缩,则考虑收缩测量结果可大大改进热粘性-弾性模型。改进方法是将理论模型用作与收缩测量数据相关的混合模型的一个独立变量,以便减小测得的收缩和预测的收缩之间的误差。由此生成的模型称作修正的模内残余应力 (CRIMS) 模型。
构想如下所示:
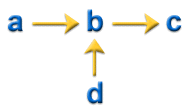
修正的残余模内应力 (CRIMS) 模型
(a) 预测的各向同性残余应力 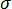 ,(b) 误差修正,(c) 修正的各向异性残余应力
,(b) 误差修正,(c) 修正的各向异性残余应力 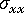 和
和 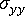 ,(d) 测量的收缩。
,(d) 测量的收缩。
为说明该模型的效果,请参考下图。
聚丙烯的平行收缩
(a) 收缩百分比,(b) 成型条件设置数, 测量的平行收缩,
测量的平行收缩, 修正的平行收缩,
修正的平行收缩, 计算的临界值(各向同性)。
计算的临界值(各向同性)。
此图显示了测量到的聚丙烯平行于流向的实验收缩值。还显示了计算出的理论平行收缩值(使用热粘性-弾性模型)以及修正后的平行收缩值。很明显,修正值与测量值相当一致。如下图所示,同一聚丙烯材料在垂直方向上也可取得相似的改进。
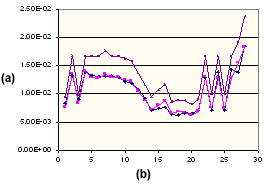
聚丙烯的垂直收缩
(a) 收缩百分比,(b) 成型条件设置数, 测量的垂直收缩,
测量的垂直收缩, 修正的垂直收缩,
修正的垂直收缩, 计算的临界值(各向同性)。
计算的临界值(各向同性)。
修正概念也可应用于纤维填充材料,结果同样很理想。下图为玻璃强化纤维占 15% 重量的 PA66 所得结果。
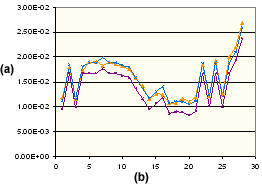
含 15% 玻璃纤维的 PA66 的平行收缩
(a) 收缩百分比,(b) 成型条件设置数, 测量的平行收缩,
测量的平行收缩, 修正的平行收缩,
修正的平行收缩, 理论平行收缩。
理论平行收缩。
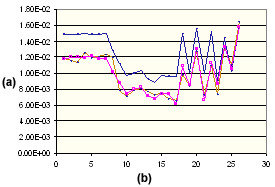
含 15% 玻璃纤维的 PA66 的垂直收缩
(a) 收缩百分比,(b) 成型条件设置数, 测量的垂直收缩,
测量的垂直收缩, 理论垂直收缩,
理论垂直收缩, 修正的垂直收缩
修正的垂直收缩
使用单变量分析时应用此方法
单变量分析是 Autodesk Moldflow 翘曲分析产品所提供的一项技术,用于确定导致翘曲的主要原因,能够采取相应措施降低零件翘曲。单变量分析主题对其进行详细介绍。本文中,我们将考虑如何在单变量分析环境下应用残余应力方法。
填充和保压阶段的填充+保压分析输出以下信息作为残余应力计算的输入:
- 局部单元轴系统中每个单元上的广义力数据,即膜力 (
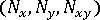 ) 和弯矩 (
) 和弯矩 (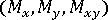 ),
), - 每个单元的材料取向角,
- 每个单元的机械特性(纵向杨氏模量、横向杨氏模量和泊松比)。
单变量分析以翘曲原因分为以下三类这一概念为基础:
- 冷却不均,
- 收缩不均,
- 取向效应。
此项概念只考虑收缩,不考虑应力。因此,为使用残余应力模型找出涉及以上三种效应的翘曲原因,我们需要根据给定的广义力计算广义应变,然后将应变分解为分别与冷却不均、收缩不均和取向效应相关的三个部分,然后将修正后的应变转化回对应的广义力。然后单独执行每种应力分析以获取每种效应的翘曲结果。相关的计算方程总结如下。
针对横向各向同性材料(机械特性在与纤维轴(即轴 1)垂直的所有平面中都有各向同性)的胡克定律可表示为:
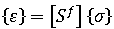
其中
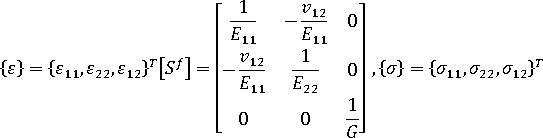
柔度矩阵按下式给出
胡克定律也可写成如下刚度矩阵形式
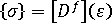
使用
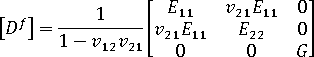
在给定的材料取向角 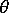 的情况下,我们将柔度矩阵和刚度矩阵从取向系统变换到局部单元系统。
的情况下,我们将柔度矩阵和刚度矩阵从取向系统变换到局部单元系统。
广义应变按下式给出
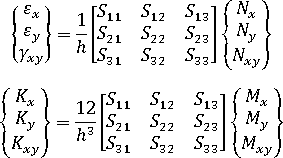
其中,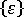 和
和 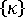 分别是应变和曲率向量。
分别是应变和曲率向量。
以下方程将应变和曲率转化回膜力和弯矩:
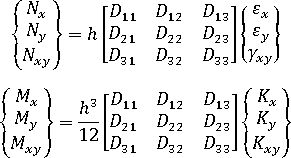
为了区分翘曲效应,我们用各分解分量替换 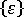 和
和 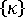 ,然后重新计算膜力和弯矩并在结构分析中使用新值。
,然后重新计算膜力和弯矩并在结构分析中使用新值。