一般計算公式
彈簧外徑
D 1 = D + d [in]
其中:
|
D |
彈簧平均直徑 [in] |
|
|
d |
線材直徑 [in] |
彈簧內徑
D 2 = D - d [in]
其中:
|
D |
彈簧平均直徑 [in] |
|
|
d |
線材直徑 [in] |
預載彈簧的扭矩
![]()
其中:
|
F 1 |
預載彈簧的工作力 [lb] |
|
|
R 1 |
工作力力臂 [in] |
滿載彈簧的扭矩
![]()
其中:
|
F 8 |
工作力 (對於滿載彈簧) [lb] |
|
|
R 1 |
工作力力臂 [in] |
彈簧指數
i = D/d [-]
其中:
|
D |
彈簧平均直徑 [in] |
|
|
d |
線材直徑 [in] |
工作行程角度
ϕ h = ϕ 8 - ϕ 1 [°]
其中:
|
ϕ 8 |
滿載彈簧的工作臂角度撓曲 [°] |
|
|
ϕ 1 |
預載狀態的工作臂角度撓曲 [°] |
最小工作臂角度撓曲
![]()
其中:
|
M 1 |
預載彈簧的扭矩 [lb ft] |
|
|
k |
扭轉彈簧剛性係數 [lb ft/°] |
|
|
ϕ h |
工作行程角度 [°] |
|
|
M 8 |
滿載彈簧扭矩 [lb ft] |
最大工作臂角度撓曲
![]()
其中:
|
M 1 |
預載彈簧的扭矩 [lb ft] |
|
|
k |
扭轉彈簧剛性係數 [lb ft/°] |
|
|
ϕ h |
工作行程角度 [°] |
|
|
M 8 |
滿載彈簧扭矩 [lb ft] |
應力集中係數
![]()
其中:
|
i |
彈簧指數 [-] |
|
|
i = D/d [-] |
用於計算有效圈數折彎應力 |
|
|
|
用於計算臂折彎應力 |
|
|
r |
臂 (內部) 折彎半徑 [in] |
|
|
d |
線材直徑 [in] |
一般情況下的彈簧材料應力
![]()
其中:
|
M |
一般情況下的彈簧扭矩 [Nm] |
|
|
K f |
應力集中係數 [-] |
|
|
d |
線材直徑 [in] |
彈簧作用中螺旋數
![]()
其中:
| ϕ |
一般情況下的工作臂角度撓曲 [°] |
|
|
E |
彈性係數 [psi] |
|
|
d |
線材直徑 [in] |
|
|
M |
一般情況下的彈簧扭矩 [lb ft] |
|
|
R 1 |
工作力力臂 [in] |
|
|
R 2 |
支撐力力臂 [in] |
|
|
D |
彈簧平均直徑 [in] |
彈簧設計計算
設計彈簧期間,會設計線材直徑、螺旋數及彎鉤臂彎曲直徑,以符合特定負載、材料和組合標註。設計彈簧以符合建議使用的線材徑。對於螺旋間存在間隙的彈簧,自由狀態下彈簧螺紋之間的節距 t 必須在 0.3 D ≤ t ≤ 0.5 D [in] 範圍之內。
彈簧設計基於 (σ 8 ≤ u s sA) and (σ 8r ≤ u s σ A ) 強度條件和某些彈簧幾何標註的建議範圍。
L Z ≤ 10 D and L Z ≤ 31.5 in and 4 ≤ D/d ≤ X and n≥ 1.5 and 1.2 d ≤ t < D and r ≥ d。
其中:
- 彈簧含緊密纏繞螺旋 X = 16
- 彈簧含鬆散纏繞螺旋 X = 10
根據指定的造型和臂長度,彈簧標註符合可行的幾何解決方案。如果規格中已設定裝配限制標註 (容許的最大罩直徑和長度或容許的最大桿直徑),這些標註必須符合裝配限制標註。
指定的最大負載、材料和彈簧組合標註
首先,檢查並計算用於計算的輸入值。
然後,針對指定的最大負載和組合標註計算最小負載。
![]()
其中:
|
M 1 |
預載彈簧的扭矩 [lb ft] |
|
|
M 8 |
滿載彈簧扭矩 [lb ft] |
|
|
ϕ 1 |
預載狀態的工作臂角度撓曲 [°] |
|
|
ϕ 8 |
滿載彈簧的工作臂角度撓曲 [°] |
設計線材直徑和圈數,以在計算彈簧直徑後,能夠滿足強度和幾何條件。如果規範中已限定彈簧直徑值,則彈簧設計必須符合此條件。否則,可透過容許的最小與最大線材直徑幾何條件決定彈簧直徑限制。
對於帶鉤臂的彈簧,設計合適的臂折彎半徑。
從最小線材直徑開始到最大線材直徑,計算具有指定強度和幾何條件的所有彈簧線材直徑。然後,測試是否符合合適簧圈數的所有所需條件。如果所有條件都符合,會使用選取的值 (不管是否還有其他符合條件的彈簧線材直徑) 完成設計,並採用最小可能線材直徑、最少螺旋數以及最小彈簧直徑設計彈簧。
指定的負載、材料和工作撓曲角度
首先,檢查用於計算的輸入值。
接下來,針對指定的負載和工作撓曲角度,計算工作臂角度撓曲。
工作臂的最小撓曲
![]()
工作臂的最大撓曲
![]()
其中:
|
M 1 |
預載彈簧的扭矩 [lb ft] |
|
|
M 8 |
滿載彈簧扭矩 [lb ft] |
|
|
ϕ 1 |
預載狀態的工作臂角度撓曲 [°] |
|
|
ϕ 8 |
滿載彈簧的工作臂角度撓曲 [°] |
|
|
ϕ h |
工作行程角度 [°] |
接下來,設計線材直徑和螺旋數,以在計算彈簧直徑後,能夠滿足強度和幾何條件。如果規範中已限定彈簧直徑值,則彈簧設計必須符合該條件。否則,可透過容許的最小與最大線材直徑幾何條件決定彈簧直徑限制。
對於帶鉤臂的彈簧,設計合適的臂折彎半徑。
從最小線材直徑開始到最大線材直徑,考慮具有指定強度和幾何條件的所有彈簧線直徑。接下來,測試是否符合合適簧圈數的所有所需條件。如果所有條件都符合,會使用選取的值 (不管是否還有其他符合條件的彈簧線材直徑) 完成設計,並採用最小可能線材直徑、最少螺旋數以及最小彈簧直徑設計彈簧。
指定的最大負載、材料和彈簧直徑
首先,檢查要計算的輸入值。
接下來,設計線材直徑、螺旋數及組合標註,以滿足強度和幾何條件。如果規範中已限定工作撓曲角度值,則彈簧設計必須符合此條件。否則,可透過指定的彈簧直徑以及允許的最小與最大線材直徑的幾何條件,確定組合標註的極限。
對於帶鉤臂的彈簧,計算合適的臂折彎半徑。
會考量具有指定強度和幾何條件的所有彈簧線材直徑,並將線材直徑按從小到大的遞增順序計算各個設計。接下來,測試是否符合簧圈數的所有所需條件。如果所有條件都符合,會使用選取的值 (不管是否還有其他符合條件的彈簧線材直徑) 完成設計,並採用最小可能線材直徑、最少螺旋數以及最小彈簧直徑設計彈簧。
指定的最大負載、材料、彈簧直徑和工作撓曲角度
首先,檢查要計算的輸入值。
接下來,最佳化材料直徑、螺旋數及工作臂的角度撓曲,以滿足強度和幾何條件。考量到工作臂 ϕ 1 的最小角度撓曲 (約等於 2°) 要求,程式尋求工作臂 ϕ 8 的最大角度撓曲的最小值。
對於帶鉤臂的彈簧,計算合適的臂折彎半徑。
最後,針對指定的最大負載和設計出的工作臂角度撓曲,計算最小彈簧負載。
![]()
其中:
|
M 1 |
預載彈簧的扭矩 [lb ft] |
|
|
M 8 |
滿載彈簧扭矩 [lb ft] |
|
|
ϕ 1 |
預載狀態的工作臂角度撓曲 [°] |
|
|
ϕ 8 |
滿載彈簧的工作臂角度撓曲 [°] |
彈簧檢查計算
針對指定的負載、材料和彈簧標註,計算相應的組合標註值。首先,檢查並計算輸入資料,然後使用以下公式計算組合標註。
最小工作臂角度撓曲
![]()
其中:
|
M 1 |
預載彈簧的扭矩 [lb ft] |
|
|
D |
彈簧平均直徑 [in] |
|
|
n |
有效圈數 [-] |
|
|
R 1 |
工作力力臂 [in] |
|
|
R 2 |
支撐力力臂 [in] |
|
|
E |
彈性係數 [psi] |
|
|
d |
線材直徑 [in] |
最大工作臂角度撓曲
![]()
其中:
|
M 1 |
預載彈簧的扭矩 [lb ft] |
|
|
D |
彈簧平均直徑 [in] |
|
|
n |
有效圈數 [-] |
|
|
R 1 |
工作力力臂 [in] |
|
|
R 2 |
支撐力力臂 [in] |
|
|
E |
彈性係數 [psi] |
|
|
d |
線材直徑 [in] |
工作行程角度
ϕ h = ϕ 8 - ϕ 1 [°]
其中:
|
M 8 |
滿載彈簧扭矩 [lb ft] |
|
|
ϕ 8 |
滿載彈簧的工作臂角度撓曲 [°] |
計算工作力
針對指定的材料、組合標註和彈簧標註,計算處於其工作狀態的彈簧產生的相應力。檢查並計算輸入資料,然後使用以下公式計算工作力。
最小工作負載
![]()
![]()
其中:
|
M 1 |
預載彈簧的扭矩 [lb ft] |
|
|
ϕ 1 |
預載狀態的工作臂角度撓曲 [°] |
|
|
D |
彈簧平均直徑 [in] |
|
|
n |
有效圈數 [-] |
|
|
R 1 |
工作力力臂 [in] |
|
|
R 2 |
支撐力力臂 [in] |
|
|
E |
彈性係數 [psi] |
|
|
d |
線材直徑 [in] |
最大工作負載
![]()
![]()
其中:
|
M 8 |
滿載彈簧扭矩 [Nm] |
|
|
ϕ 8 |
滿載彈簧的工作臂角度撓曲 [°] |
|
|
D |
彈簧平均直徑 [in] |
|
|
n |
有效圈數 [-] |
|
|
R 1 |
工作力力臂 [in] |
|
|
R 2 |
支撐力力臂 [in] |
|
|
E |
彈性係數 [psi] |
|
|
d |
線材直徑 [in] |
計算彈簧輸出參數
可用於所有類型的彈簧計算,並按照以下順序進行計算。
扭轉彈簧率
![]()
鬆彈簧的螺旋間距
a = t - d [mm]
鬆彈簧的彈簧螺旋部分長度
|
對於纏繞緊密的彈簧 |
|
|
L 0 = (1.05 n + 1) d [in] |
|
|
對於纏繞鬆散的彈簧 |
|
|
L 0 = t n + d [in] |
|
最小工作負載下作用中螺旋中彈簧材料的彎曲應力
![]()
其中,計算 i = D/d 時的應力集中係數 K f
最小工作負載下臂彎曲處彈簧材料的彎曲應力
![]()
其中,計算 i = 2r/d + 1 時的應力集中係數 K f
滿載狀態下作用中螺旋中彈簧材料的彎曲應力
![]()
其中,計算 i = D/d 時的應力集中係數 K f
滿載狀態下臂彎曲處彈簧材料的彎曲應力
![]()
其中,計算 i = 2r/d + 1 時的應力集中係數 K f
滿載狀態下的緊密纏繞彈簧的螺旋彈簧部分的長度與負載盤繞彈簧
![]()
滿載狀態下的彈簧外徑與負載盤繞彈簧
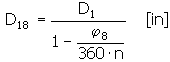
滿載狀態下的彈簧內徑與負載盤繞彈簧
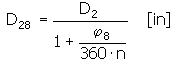
工作臂極限測試角度撓曲
![]()
彈簧變形能量
![]()
線材長度
|
l = 3.2 D n + l R [in] |
||||
|
其中,l R 是臂長,前提條件是: |
||||
|
其中,l R 是臂長,前提條件是: |
||||
|
直扭力臂長度 |
||||
|
|
||||
|
鉤臂長度 |
||||
|
|
||||
彈簧質量
![]()
檢查彈簧負載
(σ 8 ≤ u s σ A ) and (σ 8r ≤ u s σ A )
所用變數的含義:
|
a |
自由狀態下有效圈數的間距 [in] |
|
d |
線材直徑 [in] |
|
D |
彈簧平均直徑 [in] |
|
D 1 |
彈簧外徑 [in] |
|
D 2 |
彈簧內徑 [in] |
|
E |
彈性係數 [psi] |
|
F |
一般情況下彈簧施加的工作力 (施加在工作力臂 R 1 上的力) [lb] |
|
i |
彈簧指數 [-] |
|
K F |
應力集中係數 [-] |
|
kϕ |
扭轉彈簧剛性係數 [lb ft/°] |
|
r 1 |
工作臂折彎半徑 [in] |
|
r 2 |
支撐臂折彎半徑 [in] |
|
R 1 |
工作力力臂 [in] |
|
R 2 1 |
支撐力力臂 [in] |
|
l |
線材長度 [in] |
|
L 0 |
一般情況下的簧圈部份長度 [in] |
|
m |
彈簧質量 [lb] |
|
M |
一般情況下的彈簧扭矩 [lb ft] |
|
n |
有效圈數 [-] |
|
t |
鬆弛狀態下的簧圈節距 [in] |
|
u s |
|
| ρ |
彈簧材料密度 [lb/ft3] |
| ϕ |
一般情況下的工作臂角度撓曲 [°] |
| σ |
一般情況下的彈簧材料折彎應力 [psi] |
|
σ A |
彈簧材料的容許折彎應力 [psi] |
|
M 1 |
預載彈簧的扭矩 [lb ft] |
|
M 8 |
滿載彈簧扭矩 [lb ft] |
|
ϕ 8 |
滿載彈簧的工作臂角度撓曲 [°] |
|
ϕ 1 |
預載狀態的工作臂角度撓曲 [°] |
|
ϕ 8 |
滿載彈簧的工作臂角度撓曲 [°] |
|
ϕ h |
滿載彈簧的工作臂角度撓曲 [°] |