一般計算公式
彈簧外徑
D 1 = D + d [in]
其中:
|
D |
彈簧平均直徑 [in] |
|
|
d |
線材直徑 [in] |
彈簧內徑
D 2 = D - d [in]
其中:
|
D |
彈簧平均直徑 [in] |
|
|
d |
線材直徑 [in] |
工作撓曲
H = L 8 - L 1 = s 8 - s 1 [in]
其中:
|
L 8 |
滿載彈簧的長度 [in] |
|
|
L 1 |
預載彈簧的長度 [in] |
|
|
s 8 |
滿載彈簧的撓曲 [in] |
|
|
s 1 |
預載彈簧的撓曲 [in] |
簧眼的高度
![]()
其中:
|
L 0 |
自由彈簧的長度 [in] |
|
|
L Z |
彈簧線圈部分的長度 [in] |
彈簧指數
c = D/d [-]
其中:
|
D |
彈簧平均直徑 [in] |
|
|
d |
線材直徑 [in] |
華氏 (Wahl) 更正係數
![]()
其中:
|
c |
彈簧指數 [-] |
初始拉力
![]()
其中:
|
D |
彈簧平均直徑 [in] |
|
|
d |
線材直徑 [in] |
|
|
τ 0 |
自由狀態應力 [psi] |
|
|
K w |
華氏 (Wahl) 更正係數 [-] |
彈簧施加的一般力
![]()
其中:
|
D |
彈簧平均直徑 [in] |
|
|
d |
線材直徑 [in] |
|
| τ |
扭轉應力是指一般情況下彈簧材料的每單位面積的力 [psi] |
|
|
K w |
華氏 (Wahl) 更正係數 [-] |
|
|
G |
彈簧材料的彈性係數 [psi] |
|
|
s |
彈簧常規撓曲 [in] |
|
|
n |
有效圈數 [-] |
|
|
F 0 |
彈簧初始拉力 [lb] |
彈簧常數
![]()
其中:
|
D |
彈簧平均直徑 [in] |
|
|
d |
線材直徑 [in] |
|
|
G |
彈簧材料的彈性係數 [psi] |
|
|
s |
彈簧常規撓曲 [in] |
|
|
n |
有效圈數 [-] |
|
|
F 8 |
滿載彈簧的工作力 [psi] |
|
|
F 1 |
最小負載彈簧的工作力 [psi] |
|
|
H |
工作撓曲 [in] |
彈簧設計計算
在彈簧設計範圍內,線材直徑、螺旋數和彈簧自由長度 L 0 是為特定負載、材料和組合標註而設定的。
![]()
如果計算的彈簧與 τ 0 應力的所有線材直徑均不相符 (根據公式),則將在建議範圍內使用自由狀態下修正的應力值重複進行彈簧計算。
![]()
沒有初始拉力的彈簧是針對建議的平均節距值 t = 0.35 D [in] 設計的。
如果計算的彈簧與所選節距的任何線材直徑不相符,則在建議範圍 0.3 D ≤ t ≤ 0.4 D [in] 內使用修正節距值重複進行彈簧計算。
彈簧設計以 τ 8 ≤ u s τ A 強度條件和某些彈簧幾何標註的建議範圍為基礎:L 0 ≤ D and L 0 ≤ 31.5 in and 4 ≤ D/d ≤ 16 and n ≥ 2。
指定的負載、材料和彈簧組合標註
首先,檢查並計算用於計算的輸入值。
接下來,計算自由狀態下的彈簧長度。
![]()
計算後,設計線材直徑、螺旋數和彈簧直徑,以使彈簧鉤的高度符合選取的鉤類型,並滿足強度和幾何條件。彈簧設計必須符合規範中所限制的任何彈簧直徑值。
在設計程式中,按照從小到大的順序,計算符合強度和幾何條件的所有彈簧材料直徑。測試彈簧鉤高度和線圈數。如果所有條件均滿足,設計將以選取的值結束,而不考量其他符合的彈簧線材直徑。
計算的彈簧鉤高度必須在 d ≤ o ≤ 30 d 範圍內。線材直徑、線圈數和彈簧直徑的組合必須最終使計算出的彈簧鉤高度與基本鉤類型的高度相符。基本鉤類型的選取步驟如下,首先考察完整迴路,然後考察內部完整迴路,接著再考察其他鉤類型。
指定的負載、材料和彈簧直徑
首先,檢查要計算的輸入值。
檢查後,設計線材直徑、螺旋數和彈簧自由長度和組合標註,以使彈簧鉤的高度符合所選的鉤類型。還必須滿足強度和幾何條件。如果在規範中描述了組合標註 L 1 或 L 8 ,或者工作彈簧撓曲值受到限制,則彈簧設計必須符合此條件。否則,組合標註和彈簧自由長度的極限,由上述指定彈簧直徑的幾何條件和允許的最小或最大線材直徑決定。
使用指定線材直徑設計彈簧的公式。

其中,τ 8 = 0.85 τ A 值用於計算彈簧滿載狀態下,彈簧材料的扭轉應力值。
如果無法為此線材直徑設計合適的彈簧標註組合,幾何考察將接著在所有合適的彈簧線材直徑中進行。按照從小到大的順序測試彈簧線材直徑,直到找到的彈簧鉤高度符合上述條件的線圈數。使用選取的值完成設計,而不考慮其他適合的彈簧線材直徑,並且以最小的線材直徑和最小的圈數設計彈簧。
計算的彈簧鉤高度必須在 d ≤ o ≤ 30 d 範圍內。根據由此方法計算的鉤高度選取相應的鉤類型¡C線材直徑、線圈數、彈簧自由長度和組合標註的組合必須最終使計算出的彈簧鉤高度與基本鉤類型的高度相符。基本鉤類型的選取步驟如下,首先考察完整迴路,然後考察內部完整迴路,接著再考察其他鉤類型。
指定的最大工作力、確定的材料、組合標註及彈簧直徑
首先,檢查並計算用於計算的輸入值。
然後,設計線材直徑、螺旋數和彈簧自由長度和最小工作力 F 1 ,以使彈簧鉤的高度符合所選的鉤類型。此外,還必須滿足上述強度和幾何條件。
使用指定線材直徑設計彈簧的公式。

其中,τ 8 = 0.9 τ A 值用於計算彈簧滿載狀態下,彈簧材料的扭轉應力值。
如果無法為此線材直徑設計合適的彈簧標註組合,幾何考察將接著在所有合適的彈簧線材直徑中進行。按照從小到大的順序測試彈簧線材直徑,直到找到的彈簧鉤高度符合上述條件的線圈數。使用選取的值完成設計,而不考慮其他適合的彈簧線材直徑,並且以最小的線材直徑和最小的圈數設計彈簧。
彈簧檢查計算
計算組合標註的相應值和指定負載、材料及彈簧標註的工作撓曲。
首先,檢查用於計算的輸入值。然後,使用以下公式計算組合標註。
預載彈簧的長度
![]()
滿載彈簧的長度
![]()
其中:
|
F 1 |
最小負載彈簧的工作力 [psi] |
|
|
D |
彈簧平均直徑 [in] |
|
|
d |
線材直徑 [in] |
|
|
G |
彈簧材料的彈性係數 [psi] |
|
|
L 0 |
自由彈簧的長度 [in] |
|
|
n |
有效圈數 [-] |
|
|
F 8 |
滿載彈簧的工作力 [psi] |
工作撓曲
H = L 1 - L 8 [in]
計算工作力
計算彈簧在其工作狀態時對指定材料、組合標註和彈簧標註所產生的相應力。首先,檢查並計算輸入資料,然後使用以下公式計算工作力。
最小工作力
![]()
最大工作力
![]()
計算彈簧輸出參數
可用於所有類型的彈簧計算,並按照以下順序進行計算。
鉤高度係數
![]()
彈簧常數
![]()
螺旋部分的長度
|
沒有初始拉力的彈簧 |
|
|
L z = t n + d [in] |
|
|
具有初始拉力的彈簧 |
|
|
L z = 1.03 (n + 1) d [in] |
|
預載的彈簧撓曲
s 1 = L 1 - L 0 [in]
彈簧總撓曲
s 8 = L 8 - L 0 [in]
預載狀態下彈簧材料的扭轉應力
![]()
滿載應力下彈簧材料的扭轉應力
![]()
彈簧極限力
![]()
極限狀態下的撓曲
![]()
其中:
|
k |
彈簧常數 [lb/in] |
|
|
F 9 |
極限負載的彈簧工作力 [lb] |
|
|
F 0 |
彈簧初始拉力 [lb] |
極限彈簧長度
L 9 = L 0 + s 9 [in]
彈簧變形能量
![]()
展開的線材長度
|
l = 3.2 D n + l 0 [in] |
|||
|
其中,展開的鉤長度為 l 0 : |
|||
|
對於半鉤 |
|||
|
l 0 = π D + 4 o - 2 D - 2 d [in] |
|||
|
對於完整迴路 |
|||
|
l 0 = 2 (π D - 2 d) [in] |
|||
|
對於側面完整迴路 |
|||
|
l 0 = 2 (π D - 2 d) [in] |
|||
|
對於內部完整迴路 |
|||
|
l 0 = 2 (π D - d) [in] |
|||
|
對於懸空鉤 |
|||
|
l 0 = π D + 2 o - D + 3 d [in] |
|||
|
對於雙紋線完整迴路 |
|||
|
l 0 = 4 π D [in] |
|||
|
對於側面雙紋線完整迴路 |
|||
|
l 0 = 4 π D [in] |
|||
|
對於非指定的鉤類型 |
|||
|
l 0 = 0 [in] |
|||
彈簧質量
![]()
彈簧顫動的自然頻率
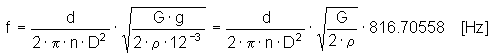
檢查彈簧負載
τ 8 ≤ u s τ A
所用變數概述:
|
d |
線材直徑 [in] |
|
k |
彈簧常數 [lb/in] |
|
D |
彈簧平均直徑 [in] |
|
D 1 |
彈簧外徑 [in] |
|
D 2 |
彈簧內徑 [in] |
|
F |
彈簧產生的一般工作力 [lb] |
|
G |
彈簧材料的剪切彈性模數 [psi] |
|
H |
工作撓曲 [in] |
|
c |
彈簧指數 [-] |
|
K w |
華氏 (Wahl) 更正係數 [-] |
|
l |
拉開的線材長度 [in] |
|
L |
彈簧常規長度 [in] |
|
L Z |
彈簧螺旋部分的長度 [in] |
|
m |
彈簧質量 [lb] |
|
n |
有效圈數 [-] |
|
o |
彈簧鉤高度 [in] |
|
t |
處於自由狀態的有效圈數的間距 [in] |
|
s |
彈簧常規撓曲 (延伸) [in] |
|
u s |
|
| ρ |
彈簧材料密度 [lb/ft3] |
| τ |
扭轉應力是指一般情況下彈簧材料的每單位面積的力 [psi] |
|
τ A |
彈簧材料容許的扭轉應力 [psi] |