Weißbuch: Drehwinkel der VU IK-Berechnung

Als Grundvoraussetzung für die VU-Berechnung muss die Berechnung unabhängig vom Verlauf sein. Die Berechnung darf nur auf dem aktuellem Zustand des Ziels und der anderen Parameter basieren.

Drehwinkel – Grad der Freiheit

Wenn das Positionsziel für eine einzelne Kette angegeben wird, bleibt ein ausreichender Grad an Freiheit: die Rotation um die Endeffektorachse (EE-Achse). Der Drehwinkel wird verwendet, um diesen Grad an Freiheit quantitativ zu beschreiben.

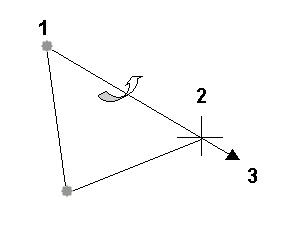
1. Anfangsgelenk

2. Endeffektor

3. EE-Achse

Berechnungsebene

Die Ebene, die alle Gelenke passiert, wird als "Berechnungsebene" bezeichnet. Wenn die Gelenke nicht auf einer Ebene liegen, wird sie als die Ebene definiert, die a) das Anfangs- und das Endgelenk passiert und b) in gewisser Hinsicht am dichtesten am anderen Gelenk liegt.

Der Drehwinkel beschreibt den Grad der Freiheit der Berechnungsebene und beeinflusst nur das Startgelenk.

Nullebenen-Map

Um die Berechnungsebene numerisch und quantitativ beschreiben zu können, müssen wir zunächst festlegen, was 0 bedeutet. Wo befindet sich die Null- (Berechnungs-)Ebene ausgehend von der Endeffektor-Position? Das Nullebenen-Map nutzt als Argument die EE-Achse und erstellt die Normale zur Nullebene.

Durch das IK-System können einzelne Berechnungs-Plug-Ins eigene Nullebenen-Maps definieren. Wenn keine Definition vorliegt, verwendet das IK-System eine Vorgabedefinition.

Beim Argument des Nullebenen-Maps handelt es sich um einen Einheitsvektor in Richtung der EE-Achse. Entsprechend sollte die Lösungsebene fixiert sein, wenn der EE über die EE-Achse gleitet. Aus diesem Grund definiert das Nullebenen-Map ein Vektorfeld auf einer Kugel. Von einem Punkt auf der Kugel aus erstellt es einen tangentialen Einheitsvektor, der als Normale zur Nullebene zu interpretieren ist.

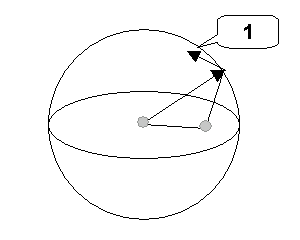
1. Normale zur Nullebene

Umkehren von Berechnungsebenen

Es ist eine mathematische Tatsache, dass auf einer Kugel kein kontinuierliches Vektorfeld möglich ist. So sehr Sie sich auch anstrengen, es wird auf der Kugel immer einen Punkt geben, an dem benachbarte Vektoren sich dramatisch verändern. An dieser Stelle kehrt sich die Berechnungsebene um, wenn die Endeffektorachse sich ihr nähert.

Dies liegt einerseits daran, dass es aufgrund der verlaufsunabhängigen Anforderungen nötig ist, diesem einzigartigen Punkt einen festen Vektor zuzuordnen. Andererseits wird dieser Vektor, unabhängig davon, um was für einen Vektor es sich handelt, sich dramatisch von den benachbarten Vektoren unterscheiden.

Inhärentes Referenz-Frame für die Kugel

Um das Nullebenen-Map definieren zu können, müssen wir zunächst ein Referenz-Frame für die Kugel definieren. Dieses Referenz-Frame ist inhärent in Bezug auf die Gelenkkette.

Eine Kugel kann über ihren Mittelpunkt, die horizontale Ebene und den Meridian (den nullten Längengrad) definiert werden. Der Mittelpunkt ist dem Startgelenk zugewiesen.

Die Pose, in der alle Gelenkwinkel die bevorzugten Winkel einnehmen, ist besonders wichtig. Sie wird als "bevorzugte Pose" bezeichnet.

Wir verwenden die Berechnungsebene in der bevorzugten Pose als horizontale Ebene. Da der Drehwinkel verwendet wird, um das Startgelenk zu steuern, sind die bevorzugten Winkel am Startgelenk weniger inhärent. Es ist auch angebracht, die horizontale Ebene mit der Berechnungsebene zu definieren, die abgeleitet wird, indem dem Startgelenk Nullen und den anderen Gelenken bevorzugte Winkel zugewiesen werden.

Die EE-Achse definiert den Meridian. Die Kugel wird nun definiert wie im folgenden Bild gezeigt:

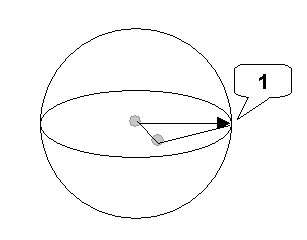
1. EE-Achse

Alle Gelenke nehmen bevorzugte Winkel ein. Das Nullebenen-Map muss auf dieser Kugel definiert werden.

Tatsächlich verwendet das API für die Plug-In-Berechnung die EE-Achse und die Normale für die Berechnungsebene in der bevorzugten Pose und definiert so ein eigenes Nullebenen-Map:

virtual const IKSys::ZeroPlaneMap*

 GetZeroPlaneMap(const Point3& a0,
 const Point3& n0) const

wobei es sich bei a0 und n0 um die EE-Achse, bzw. die Berechnungsebene in der bevorzugten Pose handelt. Bei "Objekt von ZeroPlaneMap" handelt es sich um eine Funktion, die einem jedem Punkt auf der Kugel eine Ebenennormale zuordnet.

Vorgabe-Nullebenen-Map

Wenn von den Plug-In-Berechnungen (die Berechnung ist als Plug-In-Berechnung implementiert) kein Nullebenen-Map zur Verfügung gestellt wird, bietet das IK-System ein Vorgabe-Nullebenen-Map. Dieses Map wird über die folgenden Regeln definiert:

• A: Für jeden Punkt auf dem Äquator, den Schnittpunkt der horizontalen Ebene und die Kugel ist der Normalenvektor als der vertikale Vektor definiert, der in dieselbe Richtig zeigt wie die Normale der Berechnungsebene in der bevorzugten Pose.
• B: Für jeden Punkt auf der Kugel außer dem Nord- und Südpol gibt es einen großen Kreis, der den Punkt und den Nord- und Südpol passiert. Dieser Kreis schneidet den Äquator in zwei Punkten. Ein Punkt liegt näher an dem bestimmten Punkt. Der Normalenvektor an dem bestimmten Punkt wird definiert als der Vektor, der entsteht, wenn die Normale am Punkt, der näher am Äquator liegt, tangential am großen Kreis entlang zum Punkt bewegt wird.
  

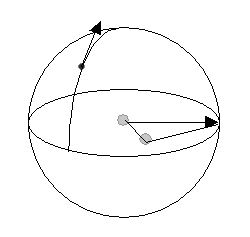
  Ableiten der Vorgabe-Normalen zur Nullebene

Diese Methode lässt sich natürlich nicht auf den Nord- und Südpol übertragen. Bei ihnen handelt es sich um einzigartige Punkte. Wenn die EE-Achse über die Pole bewegt wird, ändert die Normale plötzlich ihre Richtung und dreht sich aus dem Blickfeld des Benutzers.

Normalerweise handelt es sich bei der bevorzugten Pose um jene von der ersten Zuweisung der Berechnung. Die Ebene, auf der die Gelenke liegen entspricht hier also der horizontalen Ebene. Regel A stellt sicher, dass die Kette auf der Ebene bleibt, wenn das Ziel auf der Ebene verschoben wird.

Regel B bedeutet, dass die Kette vertikal bleibt, wenn das Ziel entlang des großen Kreises vertikal zum Äquator verschoben wird, außer wenn es die Pole passiert, bei denen es sich um die einzigartigen Punkte dieses Maps handelt.

Übergeordneter Raum

Bisher wurde alles so beschrieben, als ob es in der Welt nur IK-Elemente gäbe. In Realität können sich die IK-Kette und das Ziel in unterschiedlichen Transformationshierarchien befinden. Schließlich müssen Sie die Position des Endeffektors festlegen, der in der Welt einem Punkt auf der Kugel zugeordnet ist. Je nachdem, wie die Kugel im Verhältnis zum Endeffektor befestigt ist, unterscheiden sich die Lesarten für die Breiten- und Längengrade. Der übergeordnete Transformationsraum, in dem diese Kugel platziert werden muss, wird als übergeordneter Drehpunktraum oder, wenn der Kontext eindeutig ist, als übergeordneter Raum bezeichnet.

Der übergeordnete Raum muss bezüglich der IK-Parameter unveränderlich sein. Nun gibt es zwei Auswahlmöglichkeiten:

• Anfangsgelenk Der übergeordnete Drehwinkelraum entspricht dem übergeordneten Raum des Anfangsgelenks.
• IK-Ziel Der übergeordnete Drehwinkelraum ist der übergeordnete Raum des IK-Ziels.

Beispiel 1

Wenn sowohl das Anfangsgelenk als auch das Ziel direkt in der Welt verwurzelt sind, treten bei der Auswahl des übergeordneten Raums keine Unterschiede auf. Im folgenden Beispiel ist das Anfangsgelenk dem Objekt A übergeordnet.

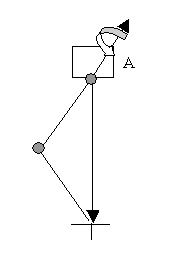
Die IK-Kette ist (über das Anfangsgelenk) bei Objekt A übergeordnet.

Nehmen Sie an, dass es sich hierbei um die Pose handelt, in der die IK-Berechnung zugewiesen wird. Es handelt sich also um die bevorzugte Pose. Bei der Ebene, auf der die Gelenke ausgelegt werden, handelt es sich um die horizontale Ebene der (Nullebenen-Map-) Kugel.

• A: Beim übergeordneten Raum handelt es sich um das Anfangsgelenk. In diesem Fall ist die Kugel A übergeordnet. Wenn A um die gezogene Achse gedreht wird, dreht sich die Kugel mit. Das Ziel befindet sich in einer anderen Transformationshierarchie. Es bleibt an diesem Platz, und der Endeffektor bleibt aufgrund der IK-Berechnung am Ziel. Da die (Ebenen-) Normale auf der Kugel fixiert ist, dreht auch sie sich mit A. Aus diesem Grund scheint die gesamte Kette sich mit dem übergeordneten Objekt zu drehen.
• B: Beim übergeordneten Raum handelt es sich um das IK-Ziel. Wir nehmen an, dass das Ziel der Welt übergeordnet ist. In diesem Fall ist die Kugel der Welt übergeordnet und bleibt folglich stationär. Da die Normale auf der Kugel fixiert ist, wirkt die Kette, als ob sie fest wäre, wenn A gedreht wird.

Beispiel 2

Im folgenden Beispiel betrachten wir einen Fall, in dem eine Drehung im übergeordneten Raum mit zugewiesener Berechnung stattfindet.

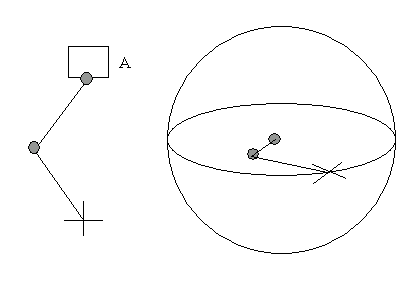
Der übergeordnete Raum der IK-Kette enthält eine Drehung, wenn die IK-Berechnung zugewiesen ist.

Das übergeordnete Objekt A umfasst eine Drehung um 90 Grad. Es handelt sich hier um eine Abstraktion des Falls, in dem ein Benutzer vier Bones ohne IK-Berechnung erstellt und später den Bones 2 bis 4 eine IK-Berechnung zuweist. Wenn wir die Kette der Welt direkt überordnen, könnte dies aussehen wie im rechten Bild: die Berechnungsebene wird horizontal.

• A: Beim übergeordneten Raum handelt es sich um das Anfangsgelenk. Die Kugel wird nach der Drehung von A befestigt. Aus diesem Grund stimmt die "horizontale Ebene" mit der im Ansichtsfenster angezeigten Kettenebene überein. Die einzigartigen Punkte bilden bezüglich der Ebene einen rechten Winkel zum Anfangsgelenk. Wenn der Ziel- oder Endeffektor auf der Ebene verschoben wird, trifft er nie die einzigartigen Punkte und kehrt sich aus diesem Grund auch nicht um.
• B: Beim übergeordneten Raum handelt es sich um das IK-Ziel. Wir gehen wieder davon aus, dass es sich beim übergeordneten Raum des Ziels um die Welt handelt. Die "horizontale Ebene" der Kugel wird horizontal, wie im rechten Bild zu sehen ist. Die einzigartigen Punkte, die Pole, befinden sich auf der Ebene, auf der die Gelenke ausgelegt sind. Aus diesem Grund bewegt sich der Ziel- oder Endeffektor, wenn er nach links oder rechts oder eine andere Richtung verschoben wird, über die einzigartigen Punkte und kehrt sich um.

Ein Problem bei B liegt darin, dass das rechte Bild dem Benutzer nie gezeigt wird. Er muss es sich gedanklich vorstellen, um zu verstehen, warum der Endeffektor sich dreht.

Beispiel 3

In diesem Beispiel wird beschrieben, was passiert, wenn das Anfangsgelenk neu zugewiesen wird. Nehmen Sie an, wir hätten eine IK-Kette für vier Bone-Knoten.

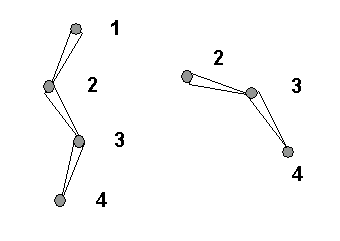
1. Bone01

2. Bone02

3. Bone03

4. Bone04

Bei Bone01 und Bone04 handelt es ich um das Anfangs- bzw. das Endgelenk. Angenommen, bei der Pose im Bild handelt es sich um die bevorzugte Pose und Bone01 umfasst eine Drehung. Wenn wir Bone02 der Welt direkt überordnen, wird die Hierarchie von Bone02 wie im Bild rechts angezeigt.

Wenn wir das Anfangsgelenk nun Bone02 erneut zuweisen, wird die Nullebenen-Map-Kugel auf der Konfiguration rechts aufgebaut.

• A: Beim übergeordneten Raum handelt es sich um das Anfangsgelenk. In diesem Fall muss die Kugel, die an der Konfiguration rechts fixiert ist, auch Bone01 übergeordnet sein. Sie ist identisch mit der auf Bone01 bis Bone04 aufgebauten Kugel. Aus diesem Grund erhalten wir dieselbe Normale und die Kette bleibt stationär.
• B: Beim übergeordneten Raum handelt es sich um das IK-Ziel. In diesem Fall bleibt die Kugel in der Welt, während Bone02 Bone01 übergeordnet wird. Wenn Bone04 dorthin verschoben wird, wo er links aufgrund der Transformation von Bone01 angezeigt wird, sieht der Beobachter, der auf der Kugel fixiert ist, die wiederum auf der Welt fixiert ist, dass Bone04 sich von der neutralen Position wegbewegt, die durch die bevorzugte Pose definiert ist. Der Algorithmus wendet dann das Nullebenen-Map an, um die Normale an der verschobenen Stelle zu suchen. Im Allgemeinen ist sie nicht rechtwinklig zum Ansichtsfenster. Aus diesem Grund sehen Sie eine Drehung, wenn sie ein neues Anfangsgelenk annimmt.

Wenn Sie die Berechnung/das Ziel löschen und diese für Bone02 bis Bone04 neu zuweisen, sehen Sie, dass die Kette sich nicht umkehrt. Warum? Es besteht ein Unterschied zwischen der Zuweisung des Anfangsgelenks und der Erstellung einer neuen IK-Kette oder eines neuen IK-Ziels. Das Anfangsgelenk ist einer von vielen IK-Parametern. Bei einer neuen Zuweisung handelt es sich um nichts anderes als um die Bearbeitung eines beliebigen Parameters. Die übrigen Parameter bleiben unverändert. Insbesondere wird der Drehwinkel durch diese neue Zuweisung nicht geändert.

Bei der Erstellung einer neuen IK-Kette oder eines neuen IK-Ziels handelt es sich um einen anderen Vorgang. Die Gelenkkette soll durch eine entsprechende Anpassung der Parameter möglichst stabil gehalten werden. Insbesondere wird für den Drehwinkel ein Wert festgelegt, aufgrund dessen die Berechnungsebene im Ansichtsfenster stationär bleibt.