Der letzte Teil der kohäsiven Konstitutivbeziehung, der definiert werden muss, ist der Ausdruck für die Entwicklung der skalaren Schädigungsvariable D.

Das Schadensentwicklungsmodell muss in der Lage sein, die Entwicklung der Schädigungsvariable D vom anfänglichen Wert 0 bis zum endgültigen Wert 1 unabhängig vom genauen Verlauf der kombinierten Belastung, die durch das kohäsive Material aufrechterhalten wird, genau auszudrücken. Beachten Sie, dass es möglich ist, ein Schadensentwicklungsmodell abhängig von der Dehnung (d. h. relative Verschiebung) oder der Spannung zu entwickeln. Für unsere anfängliche Implementierung haben wir jedoch einen dehnungsbasierten Ansatz (relative Verschiebung) gewählt. Es ist logisch und möglicherweise auch intuitiv zu vermuten, dass die Schadensentwicklung durch relative Normalen- und Scherungsverschiebungen anders verläuft. Aus Gründen der Übersichtlichkeit gehen wir jedoch davon aus, dass die Schadensentwicklung als Funktion eines einzelnen Skalarmaßes der relativen Verschiebung (bezeichnet als effektive relative Verschiebung 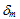) ausgedrückt werden kann, wobei

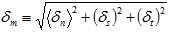
Die entsprechende effektive Zugkraft wird definiert als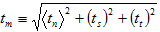

In der Abbildung oben bezeichnet 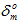den Wert der effektiven relativen Verschiebung 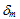bei Schadensbeginn, z. B. wenn

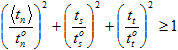
erfüllt ist. 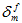bezeichnet den Wert der effektiven relativen Verschiebung 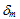, bei der die Materialsteifheit vollständig auf null abgefallen ist. 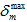bezeichnet den maximalen Wert für die effektive relative Verschiebung 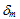, die das Material bis dahin für eine beliebige Zeit t kleiner oder gleich der aktuellen Zeit erreicht hat. Beachten Sie, dass 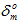und 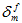Teil der Materialcharakterisierung sind.

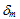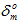
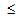
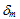
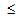
Für beliebige Werte von im Bereich 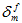kann der aktuelle Wert für die Schädigungsvariable D über die folgende Schadensentwicklungsgleichung ausgedrückt werden.

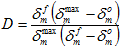
Es sollte betont werden, dass der Hauptunterschied zwischen den drei kohäsiven Konstitutivmodellen in Helius PFA die genaue Methode betrifft, mit der 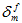zum Zwecke der Schadensentwicklungsauswertung berechnet wird. Für das Gesamtverschiebungsmodell wird der Wert von 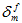berechnet, indem einfach die effektive relative Verschiebung bei Schadensbeginn 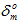zum benutzerdefinierten Parameter ( 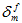- 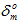) addiert wird. Wenn dann der Schadensbeginn eintritt und 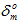bekannt ist, bleibt die effektive relative Verschiebung bei vollständiger Materialdegradation (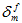) unverändert, auch wenn sich der kombinierte Belastungszustand des kohäsiven Materials ändert.

Um zu verstehen, wie 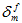für das Gesamtenergiemodell oder das Mischmodus-Potenzgesetz berechnet wird, müssen wir zunächst einige Energieausdrücke definieren. Zu einem beliebigen Zeitpunkt werden die einzelnen Energiekomponenten, die mit Normalen- und Scherungsverformungen verknüpft sind, wie folgt definiert:

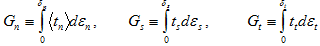
Die vom kohäsiven Material absorbierte Gesamtenergie ist einfach die Summe aus den drei Energiekomponenten

Gtotal = Gn + Gs + Gt

Wenn die Gesamtenergie Gtotal den kritischen Gesamtenergiewert erreicht, wurde das kohäsive Material vollständig auf null Steifheit degradiert und kann keine Last mehr tragen. Da wir nun den kritischen Gesamtenergiewert kennen, können wir die effektive relative Verschiebung 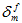berechnen, wenn das kohäsive Material wie unten gezeigt die vollständige Degradation erreicht.

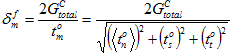
Beim Gesamtenergiemodell ändert sich nie. Es handelt sich um dieselbe benutzerdefinierte Konstante, unabhängig von der augenblicklichen Kombination aus Zugkräften, die auf das kohäsive Material angewandt werden. Für das Mischmodus-Potenzgesetz ändert sich der Wert ständig aufgrund der sich ändernden Kombination der Zugkomponenten, die auf das kohäsive Material einwirken. Im Mischmodus-Potenzgesetz kann der augenblickliche Wert ermittelt werden, indem Sie die augenblicklichen Werte Gn, Gs, und Gt gleichmäßig nach oben skalieren, bis das folgende Kriterium erfüllt ist.

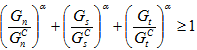
Angesichts spontaner Zugkraftstellen (tn, ts, tt) und ihrer unmittelbaren Einzelenergiedichtekomponenten (Gn, Gs, Gt) können wir das oben genannte Kriterium verwenden und diese Zugkräfte gleichmäßig nach oben skalieren, bis zu der Ebene, auf der das Kriterium erreicht ist. Bezeichnen wir diese skalierte Zugkraft mit (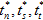) und deren entsprechende skalierte Energiekomponenten mit (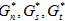). Wenn die projizierten Energiekomponenten (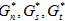), die eine Ablösungsausbreitung zur Folge hätten, angegeben sind, können wir nun die Gesamtenergie, die eine Ablösungsausbreitung zur Folge hätte, als 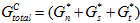berechnen.