Konstituentendurchschnittsspannungs- und -dehnungszustände
In diesem Abschnitt werden die Konstituentendurchschnittsspannungs- und -dehnungszustände für unidirektionale und gewebte Verbundwerkstoffe vorgestellt.
Es werden einfache Ableitungen dieser Mengen entwickelt und die Vorteile und Einschränkungen bei der Verwendung von Konstituentendurchschnittsgrößen erläutert.
Es bezeichne σ(x, y, z) das tatsächliche Spannungstensorfeld, das je nach Position innerhalb der Konstituentenmaterialien der heterogenen Mikrostruktur variiert. Es bezeichne D die Domäne eines repräsentativen Volumenelements (RVE), das für die Charakterisierung der Verbundmaterialreaktion an einem Punkt ausreichend ist. Unabhängig von der Komplexität der tatsächlichen Spannungsverteilung innerhalb des RVE kann der durchschnittliche (oder homogenisierte) Spannungszustand des Verbundwerkstoffs σc innerhalb des RVE ausgedrückt werden als

wobei V das Gesamtvolumen des RVE ist. Auf ähnliche Weise lassen sich die durchschnittlichen Faser- und Matrixspannungszustände ausdrücken als

wobei Vf und Vm jeweils die Volumen der Faser- und Matrixkonstituenten innerhalb des RVE (V=Vf +Vm) sind und Df und Dm die Unterdomänen bezeichnen, die von den Faser- und Matrixkonstituenten innerhalb der RVE-Gleichung (D = Df 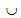 Dm) belegt sind. Das Kombinieren der Gleichungen 1-3 führt zu
Dm) belegt sind. Das Kombinieren der Gleichungen 1-3 führt zu

wobei φ f = Vf/V und φ m = Vm/V jeweils Volumenanteile der Faser- und Matrixkonstituentenmaterialien sind.
Ähnliches kann auf die Gleichungen 5-8 der Dehnungstensorstreckung unten angewendet werden.

Das grundlegende Argument für die Verwendung der Mehrphasen-Kontinuumstheorie (MCT) ist, dass die Konstituentendurchschnittsspannungs- und -dehnungszustände (σf, σm, εf, εm) viel relevanter für die Prognose von Schadensentwicklung und Materialversagen sind als die durchschnittlichen Spannungs- und Dehnungszustände von Verbundwerkstoffen (σc, εc). Schadensentwicklung und Versagen in der Matrixkonstituente werden physikalisch durch die Spannung und Dehnung in dem Material der Matrixkonstituenten gesteuert, nicht durch die Spannung und Dehnung im Material der Faserkonstituenten oder im homogenisierten Verbundmaterial. Ähnliches gilt für die Faserkonstituente.
Es ist leicht zu erkennen, dass durch die Mittelung des tatsächlichen mikromechanischen Spannungsfelds aus den einzelnen Konstituenten bessere Informationen zur Prognose von Schadensentwicklung und Versagen in Verbundwerkstoffen gewonnen werden. Allerdings sollte man die Filtermerkmale des Mittelungsprozesses für das Volumen beachten, da dieser Prozess die verschiedenen durchschnittlichen Spannungszustände einbezieht. Beginnen wir damit, ein repräsentatives Volumenelement eines unidirektionalen faserverstärkten Verbundmaterials mit einem einfachen homogenisierten Verbundspannungszustand σc zu berücksichtigen. Beispiel: ein uniaxialer Spannungszustand, bei dem 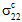 > 0 und alle anderen
> 0 und alle anderen 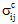 = 0. Obwohl der Durchschnittsspannungszustand des Verbundwerkstoffs uniaxial ist, ist das tatsächliche mikromechanische Spannungsfeld σ(x, y, z) innerhalb der heterogenen Mikrostruktur des RVE sehr komplex. Dies ist auf die ausgleichenden Interaktionen zwischen den Konstituentenmaterialien zurückzuführen, die durch die Unterschiede in ihren Steifheiten, Poissonschen Konstanten und thermischen Ausdehnungskoeffizienten verursacht werden. Beispiel: In dem tatsächlichen mikromechanischen Spannungsfeld erzielen vier der sechs Spannungskomponenten ( σ11, σ22, σ33, σ23) Werte ungleich null innerhalb des RVE. Darüber hinaus weisen diese vier Spannungskomponenten einen hohen Grad an räumlicher Variation gegenüber dem RVE mit zahlreichen lokalisierten Spannungskonzentrationen auf. Drei der tatsächlichen Spannungskomponenten (σ11, σ33, σ23) sind jedoch vollständig auf die selbstausgleichenden Interaktionen zwischen den Konstituentenmaterialien zurückzuführen. Beispiel: Unterschiede in den Poissonschen Konstanten von Faser und Matrix sind für die Entwicklung der selbstausgleichenden Felder σ11(x,y,z) und σ33(x,y,z) verantwortlich. Im Falle der räumlich variierenden Felder σ11(x,y,z), σ22(x,y,z) und σ33(x,y,z) muss sich Scherspannung entwickeln, damit das lokale Gleichgewicht beibehalten wird. Die Gleichungen 9-11 zeigen die partiellen Differentialgleichungen des Gleichgewichts, die für den aktuellen Fall eines unidirektionalen Verbund-RVE vereinfacht wurden, in dem alle Spannungskomponenten in Bezug auf die Faserrichtung (z. B. die Richtung '1') konstant sind.
= 0. Obwohl der Durchschnittsspannungszustand des Verbundwerkstoffs uniaxial ist, ist das tatsächliche mikromechanische Spannungsfeld σ(x, y, z) innerhalb der heterogenen Mikrostruktur des RVE sehr komplex. Dies ist auf die ausgleichenden Interaktionen zwischen den Konstituentenmaterialien zurückzuführen, die durch die Unterschiede in ihren Steifheiten, Poissonschen Konstanten und thermischen Ausdehnungskoeffizienten verursacht werden. Beispiel: In dem tatsächlichen mikromechanischen Spannungsfeld erzielen vier der sechs Spannungskomponenten ( σ11, σ22, σ33, σ23) Werte ungleich null innerhalb des RVE. Darüber hinaus weisen diese vier Spannungskomponenten einen hohen Grad an räumlicher Variation gegenüber dem RVE mit zahlreichen lokalisierten Spannungskonzentrationen auf. Drei der tatsächlichen Spannungskomponenten (σ11, σ33, σ23) sind jedoch vollständig auf die selbstausgleichenden Interaktionen zwischen den Konstituentenmaterialien zurückzuführen. Beispiel: Unterschiede in den Poissonschen Konstanten von Faser und Matrix sind für die Entwicklung der selbstausgleichenden Felder σ11(x,y,z) und σ33(x,y,z) verantwortlich. Im Falle der räumlich variierenden Felder σ11(x,y,z), σ22(x,y,z) und σ33(x,y,z) muss sich Scherspannung entwickeln, damit das lokale Gleichgewicht beibehalten wird. Die Gleichungen 9-11 zeigen die partiellen Differentialgleichungen des Gleichgewichts, die für den aktuellen Fall eines unidirektionalen Verbund-RVE vereinfacht wurden, in dem alle Spannungskomponenten in Bezug auf die Faserrichtung (z. B. die Richtung '1') konstant sind.

Die Gleichungen 10 und 11 bedeuten, dass sich die Scherspannungskomponente σ23 an einem beliebigen Punkt innerhalb des RVE entwickeln muss, wobei 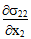 oder
oder 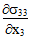 ungleich null ist. Leider werden diese selbstausgleichenden Spannungskomponenten (σ11, σ33, σ23) vollständig durch die Mittelung des mikromechanischen Spannungsfelds über das gesamte RVE hinweg herausgefiltert. Daher ist der Durchschnittsspannungszustand des Verbundwerkstoffs bei
ungleich null ist. Leider werden diese selbstausgleichenden Spannungskomponenten (σ11, σ33, σ23) vollständig durch die Mittelung des mikromechanischen Spannungsfelds über das gesamte RVE hinweg herausgefiltert. Daher ist der Durchschnittsspannungszustand des Verbundwerkstoffs bei 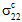 > 0.
> 0.
Dass der Durchschnittsspannungszustand des Verbundwerkstoffs σc die selbstausgleichenden Spannungskomponenten nicht darstellen kann, veranschaulicht am besten der Fall eines unabhängigen Verbundmaterials, das einer gleichmäßigen Temperaturveränderung ausgesetzt ist. In diesem Fall sind alle vier Komponenten ungleich null (σ11, σ22, σ33, σ23) des tatsächlichen Spannungsfelds σ(x,y,z) selbstausgleichend und werden aufgrund von Unterschieden bei den thermischen Ausdehnungskoeffizienten der beiden Konstituentenmaterialien verursacht. Die Durchschnittsspannung des Verbundwerkstoffs ist gleich null (σc= 0). Bei großen Temperaturveränderungen sind jedoch die Komponenten ungleich null (σ11, σ22, σ33, σ23) des tatsächlichen mikromechanischen Spannungsfelds σ(x,y,z) möglicherweise groß genug, um tatsächlich eine Schadensentwicklung oder ein Materialversagen zu verursachen.
Im Gegensatz zum zwingenden Filtern während der Berechnung von Durchschnittsspannungs- und -dehnungszuständen von Verbundwerkstoffen werden beim Berechnen der Konstituentendurchschnittsspannungs- und -dehnungszustände nur Spannungskomponenten herausgefiltert, die für das jeweilige Konstituentenmaterial selbstausgleichend sind. Es sollte betont werden, dass selbstausgleichende Normalspannungen, die durch Unterschiede bei den Poissonschen Konstanten oder thermalen Ausdehnungskoeffizienten der Konstituenten über das RVE als Ganzes hinweg selbstausgleichend sind, aber nicht für die einzelnen Konstituenten. Daher filtern die Konstituentendurchschnittsspannungszustände diese selbstausgleichenden Normalspannungen nicht heraus. Auf der anderen Seite sind die selbstausgleichenden Scherspannungen, die sich zur Beibehaltung des lokalen Gleichgewichts entwickeln, sogar innerhalb der einzelnen Konstituentenmaterialien selbstausgleichend. Aus diesem Grund filtern sowohl die Durchschnittsspannungszustände der Verbundwerkstoffe als auch die Konstituentendurchschnittsspannungszustände die selbstausgleichenden Scherspannungen heraus.
Basierend auf der vorhergehenden Beschreibung gibt die folgende Liste einen Überblick über die Filtereigenschaften der Konstituentendurchschnittsspannungszustände.
In der Regel führt die Anwendung von einer oder mehreren Durchschnittsnormalspannungen des Verbundwerkstoffs (z. B.
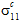 ,
, 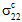 und/oder
und/oder 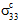 ) zu Konstituentendurchschnittsspannungszuständen, die triaxial sind (also alle drei Normalspannungen sind ungleich null). Diese Beobachtung trifft auch dann zu, wenn der Verbundspannungszustand uniaxial ist (z. B.
) zu Konstituentendurchschnittsspannungszuständen, die triaxial sind (also alle drei Normalspannungen sind ungleich null). Diese Beobachtung trifft auch dann zu, wenn der Verbundspannungszustand uniaxial ist (z. B. 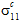 ÷ 0 und alle anderen
÷ 0 und alle anderen 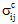 = 0). Dies ist ein direktes Ergebnis der Poissonschen Interaktionen zwischen Konstituentenmaterialien. Normalspannungen, die durch Unterschiede bei den Poissonschen Konstanten der Konstituenten erzeugt wurden, sind selbstausgleichend, wenn sie über das gesamte RVE hinweg integriert werden. Sie sind jedoch nicht selbstausgleichend, wenn sie über eine einzelne Konstituente hinweg integriert werden. Aus diesem Grund behält der Konstituentendurchschnittsspannungszustand sowohl die Normalspannungen bei, die durch externe mechanische Belastungen entstehen, als auch die Normalspannungen, die durch Poissonsche Interaktionen zwischen den Konstituenten entstehen.
= 0). Dies ist ein direktes Ergebnis der Poissonschen Interaktionen zwischen Konstituentenmaterialien. Normalspannungen, die durch Unterschiede bei den Poissonschen Konstanten der Konstituenten erzeugt wurden, sind selbstausgleichend, wenn sie über das gesamte RVE hinweg integriert werden. Sie sind jedoch nicht selbstausgleichend, wenn sie über eine einzelne Konstituente hinweg integriert werden. Aus diesem Grund behält der Konstituentendurchschnittsspannungszustand sowohl die Normalspannungen bei, die durch externe mechanische Belastungen entstehen, als auch die Normalspannungen, die durch Poissonsche Interaktionen zwischen den Konstituenten entstehen.Wenn ein unabhängiges Verbundmaterial einer gleichmäßigen Temperaturveränderung ausgesetzt ist, führen die Unterschiede bei den thermischen Ausdehnungskoeffizienten der Konstituenten zur Entwicklung von selbstausgleichenden thermischen Spannungen, wenn sie über das gesamte RVE hinweg integriert werden. Wenn sie jedoch über eine einzelne Konstituente hinweg integriert werden, sind sie nicht selbstausgleichend. In diesem Fall ist der Durchschnittsspannungszustand des Verbundwerkstoffs gleich null (σc = 0). Die durchschnittlichen Konstituentenspannungszustände sind jedoch triaxial (d. h.,
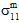 ≠ 0,
≠ 0, 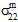 ≠ 0,
≠ 0, 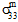 ≠ 0,
≠ 0, 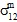 =
= 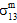 =
= 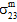 = 0 und
= 0 und 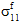 ≠ 0,
≠ 0, 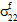 ≠ 0,
≠ 0, 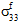 ≠ 0,
≠ 0, 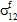 =
= 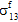 =
= 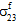 = 0).
= 0).Unidirektionale faserverstärkte Verbundmaterialien sind orthotrop (oder querisotrop) und weisen folglich keine Kopplung zwischen Normal- und Scherspannungen auf. Im Allgemeinen können Scherspannungen in Verbundmaterialien auf zwei Arten erzeugt werden. Erstens: Extern angewendete mechanische Belastungen können Scherspannungen im Verbundmaterial erzeugen. Diese Scherspannungen sind nicht selbstausgleichend. Aus diesem Grund enthalten sowohl der Durchschnittsspannungszustand des Verbundwerkstoffs (σc) als auch die Konstituentendurchschnittsspannungszustände (σf und σm) Maße dieser Scherspannungen. Zweitens: Es werden selbstausgleichende Scherspannungsfelder erzeugt, um das lokale Gleichgewicht bei normalen Spannungen beizubehalten, die eine räumliche Variation innerhalb des RVE aufweisen (gemäß den partiellen Differentialgleichungen). Diese Scherspannungen sind tatsächlich selbstausgleichend innerhalb der einzelnen Konstituentenmaterialien innerhalb des RVE. Aus diesem Grund enthalten weder der Durchschnittsspannungszustand des Verbundwerkstoffs (σc) noch die Konstituentendurchschnittsspannungszustände (σf und σm) irgendwelche Maße dieser selbstausgleichenden Scherspannungen.
Es wird allgemein angenommen, dass das tatsächliche mikromechanische Spannungsfeld σij(x,y,z) Schadensentwicklung und Versagen in den einzelnen Konstituentenmaterialien und deren Materialschnittstellen verursacht. Die Entwicklung von Modellen, die direkt das tatsächliche mikromechanische Spannungsfeld nutzen, ist jedoch ein zeitaufwändiges, komplexes und zu rechenintensives Vorhaben. In der Mehrpasen-Kontinuumstheorie liegt der Schwerpunkt stattdessen auf den Konstituentendurchschnittsspannungszuständen, bei denen das tatsächliche mikrostrukturelle Spannungsfeld σij(x,y,z) über jedes Konstituentenmaterial in der Mikrostruktur hinweg mengengemittelt wird. Um jedoch die Konstituentendurchschnittsspannungszustände in einer Strukturanalyse effektiv zu nutzen, ist es wichtig, äußerst effiziente Methoden zur Berechnung der Konstituentendurchschnittsspannungszustände zu entwickeln. Aus praktischen Gründen wird die Strukturanalyse von Verbundstrukturen durch den Durchschnittsspannungszustand des Verbundwerkstoffs formuliert. Daher erfordert die Verwendung der Konstituentendurchschnittsspannungszustände eine Methode zum Zerlegen des Durchschnittsspannungszustands des Verbundwerkstoffs in Konstituentendurchschnittsspannungszustände. Dieser als MCT-Zerlegung bezeichnete Prozess wird im folgenden Abschnitt beschrieben.