Thermische Restspannungen
Beachten Sie die Auswirkungen der thermischen Restspannungen auf unidirektionale Verbundwerkstoffe.
**Derzeit können thermische Restspannungen nur für unidirektionale Verbundmaterialien berechnet werden, nicht für gewebte Verbundmaterialien.
Mikrostruktureffekte
Bei Raumtemperatur T=Tamb verfügen die Faser- und Matrixkonstituenten einer isolierten, nicht belasteten, unabhängigen, unidirektionalen Verbundlage bereits über einen Spannungszustand ungleich null. Dies ist auf das Abkühlen des Verbundmaterials nach der Aushärtung von der Aushärtetemperatur T=Tcure auf die Umgebungstemperatur T=Tamb zurückzuführen. In einer isolierten Verbundlage werden diese thermischen Restspannungen ausschließlich durch die Unterschiede in den thermischen Ausdehnungskoeffizienten der Matrix- und Faserkonstituenten verursacht. In der Regel versucht die Matrixkonstituente während der Abkühlung nach der Aushärtung einer faserverstärkten Verbundlage mehr zu schrumpfen als die Faserkonstituente. Daher weist die Matrixkonstituente zugthermische Restspannungen und die Faserkonstituente druckthermische Restspannungen auf. Der Durchschnittsspannungszustand des Verbundwerkstoffs ist jedoch null. Diese thermischen Restspannungen der Konstituenten tragen zu den gesamten Konstituentenspannungszuständen bei allen nachfolgenden thermomechanischen Belastungen der Verbundlage bei und beeinflussen damit die Belastung, bei der Konstituentenausfälle auftreten.
Beschichtungseffekte
Wenn eine Verbundlage in eine Lage eingebettet ist, die einem Abkühlen nach Aushärtung unterzogen wird, werden zusätzliche thermische Restspannungen in die Verbundlage induziert. Dies ist zurückzuführen auf die Unterschiede zwischen den thermischen Ausdehnungskoeffizienten der betreffenden Lage und den benachbarten Lagen. Anders als bei einer isolierten Verbundlage führt diese Art von Inter-Ply-Aktion dazu, dass der Durchschnittsspannungszustand auf Lagenebene ungleich null ist, d. h., die Lage erzeugt durchschnittliche thermische Restspannungen für den Verbundwerkstoff. Diese Spannungen können in thermische Faser- und Matrixdurchschnittsrestspannungen zerlegt werden, die zur Gesamtzahl der Faser- und Matrixdurchschnittsspannungszustände bei nachfolgenden thermomechanischen Lasten beitragen. Die Spannungen haben also Einfluss auf die Lasten, bei denen die Konstituentenausfälle auftreten.
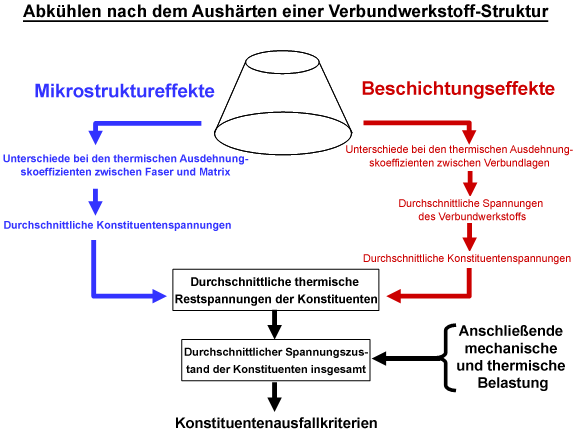
Diese beiden Quellen für thermische Restspannungen auf der Konstituentenmaterialebene werden unten schematisch dargestellt. Es wird gezeigt, dass die thermischen Restspannungen der Konstituenten zu den Konstituentenspannungen hinzugefügt werden, die durch die normalen extern angewendeten mechanischen und thermischen Belastungen der Struktur entstehen.
Berechnung der thermischen Restspannungen in Helius PFA
Die Gleichungen 32a-c beschreiben die linearisierten, thermomechanischen Konstitutivbeziehungen (Sekantenformulierung) für ein unidirektionales Verbundmaterial, das Matrixkonstituentenmaterial und das Faserkonstituentenmaterial.

In Gleichung 32a wird der gesamte Dehnungszustand des Verbundwerkstoffs an einem Punkt (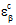 ) direkt durch den strukturellen Finite-Code angegeben, während in den Gleichungen 32b und 32c werden die gesamten Konstituentendehnungszustände an einem Punkt (
) direkt durch den strukturellen Finite-Code angegeben, während in den Gleichungen 32b und 32c werden die gesamten Konstituentendehnungszustände an einem Punkt (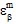 und
und 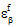 ) mithilfe der MCT-Zerlegung von
) mithilfe der MCT-Zerlegung von 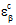 bestimmt. Bei temperaturabhängigen Verbundmaterialien sind sowohl die Steifheiten (
bestimmt. Bei temperaturabhängigen Verbundmaterialien sind sowohl die Steifheiten (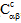 ,
, 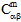 ,
, 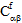 ) als auch die Koeffizienten der thermischen Ausdehnung (
) als auch die Koeffizienten der thermischen Ausdehnung (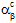 ,
, 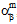 ,
, 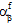 ) abhängig von der aktuellen Temperatur T und dem aktuellen Ausfallzustand der Faser- und Matrixkonstituentenmaterialien. Bei temperaturunabhängigen Verbundmaterialien sind sowohl die Steifheiten (
) abhängig von der aktuellen Temperatur T und dem aktuellen Ausfallzustand der Faser- und Matrixkonstituentenmaterialien. Bei temperaturunabhängigen Verbundmaterialien sind sowohl die Steifheiten (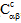 ,
, 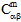 ,
, 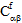 ) als auch die Koeffizienten der thermischen Ausdehnung (
) als auch die Koeffizienten der thermischen Ausdehnung (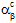 ,
, 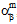 ,
, 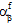 ) nur vom aktuellen Ausfallzustand der Faser- und Matrixkonstituentenmaterialien abhängig.
) nur vom aktuellen Ausfallzustand der Faser- und Matrixkonstituentenmaterialien abhängig.
In den Gleichungen 32 würde man normalerweise davon ausgehen, dass die Temperaturänderung ΔT die Differenz zwischen der aktuellen Temperatur T des Verbundwerkstoffs und der spannungsfreien Temperatur Tsf des Verbundwerkstoffs ist, d. h. ΔT = T - Tsf. Doch der eigentliche Ausdruck, den Helius PFA zur Berechnung von ΔT verwendet, hängt davon ab, ob Sie die thermischen Restspannungen berücksichtigen möchten, die während der Abkühlung des Verbundwerkstoffs nach der Aushärtung entstehen. Diese Funktion wird für jedes Verbundmaterial durch den ganzzahligen Wert der entsprechenden Benutzermaterialkonstante aktiviert und deaktiviert.
Thermische Restspannungen deaktiviert
Wenn die thermische Restspannungsfunktion deaktiviert ist, werden die thermischen Restspannungen nicht in die Reaktion des Verbundmaterials während der Simulation eingeschlossen. In diesem Fall wird die spannungsfreie Temperatur des Verbundmaterials vorgabemäßig auf Tsf = 0 ° gesetzt, und die Temperaturänderung in den Gleichungen 32 wird einfach berechnet als ΔT = T - Tsf = T. Für den Fall, dass die Berechnung der thermischen Restspannung deaktiviert ist, sollten mehrere Punkte beachtet werden.
- Die spannungsfreie Temperatur Tsf ist vorgabemäßig 0°, auch wenn die Verbundmaterialdatendatei (mdata-Datei) ausdrücklich eine spannungsfreie Temperatur ungleich null definiert. 21 Unabhängig vom verwendeten Einheitensystem im Finite-Element-Modell definiert die aktuelle Temperatur T vollständig die Temperaturänderung in ΔT in den Gleichungen 32.
- Für bei mehreren Temperaturen definierte Verbundmaterialien wird die aktuelle Temperatur T verwendet, um die in den Gleichungen 32 enthaltenen Materialeigenschaften zu interpolieren. Wenn also die thermischen Restspannungen für ein Verbundmaterial ignoriert werden, wird empfohlen, eine Einzeltemperatur-Charakterisierung (d. h., eine Einzeltemperatur-MDATA-Datei) für das betreffende Verbundmaterial zu verwenden.
Für den Fall, dass die thermischen Restspannungen ignoriert werden, lässt sich zusammenfassend sagen, dass die aktuelle Temperatur T die Gleichungen 32 auf zwei unterschiedliche Arten beeinflusst:
- T wird verwendet, um ΔT über ΔT=T zu definieren.
- T wird zum Interpolieren der aktuellen Werte für die Materialeigenschaften
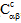 ,
, 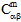 ,
, 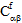 ,
, 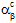 ,
, 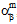 und
und 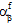 .
.
Thermische Restspannungen aktiviert
Wenn die Berechnungsfunktion für die thermische Restspannung aktiviert ist, werden die thermischen Restspannungen ausdrücklich in die Reaktion des Verbundmaterials während der Simulation eingeschlossen. In diesem Fall wird die spannungsfreie Temperatur Tsf des Verbundmaterials aus der MCT-Verbundmaterial-Datenbankdatei (MDATA-Datei) ausgelesen, wobei Tsf als Synonym für die Aushärtungstemperatur Tcure des Materials betrachtet wird. Wenn die spannungsfreie Temperatur Tsf des Materials nicht ausdrücklich in der MDATA-Datei definiert ist, gibt Helius PFA eine Fehlermeldung aus, die darauf hinweist, dass die spannungsfreie Temperatur definiert werden muss.
Wenn die Berechnungsfunktion für die thermische Restspannung aktiviert ist, gibt es zwei Methoden zum Berechnen der in Gleichung 32 verwendeten Temperaturänderung, je nachdem, ob die Materialeigenschaften für die aktuelle Temperatur verwendet werden (Vorgabe) oder ob ein eindeutiger Satz Materialeigenschaften angegeben ist.
Aktuelle Umgebung
Für den Vorgabefall, in dem die aktuellen Eigenschaften verwendet werden, wird die Temperaturänderung wie folgt berechnet:
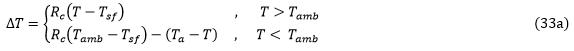
In Gleichung 33a, Tamb ist die Umgebungstemperatur. Sie wird je nach Einheitensystem des Modells als 72,5 °F, 22,5 °C oder 295,65 °K angegeben. T ist die aktuelle Temperatur und Tsf ist die spannungsfreie Temperatur.
Bei einer aktuellen Temperatur T > Tamb stellt Gleichung 33a sicher, dass die thermischen Restspannungen korrekt am Ende der Abkühlung nach der Aushärtung prognostiziert werden. Die Größe Rc kennzeichnet das Aushärtungsverhältnis. Vorgabemäßig ist Rc auf einen Wert von 0.5 festgelegt. Dieser Vorgabewert basiert auf der Arbeit von Kenik [13]. Kenik hat gezeigt, dass eine einfache lineare elastische Analyse unter Verwendung von Verbundwerkstoff-Materialeigenschaften mit Raumtemperatur mit einer festgelegten Temperaturreduzierung um die Hälfte der tatsächlichen Abkühlung nach der Aushärtung thermische Restspannungen bei den Konstituenten ergibt, die ungefähr identisch sind mit den Spannungen, die mithilfe einer gründlicheren mikromechanischen Simulation der Abkühlung nach der Aushärtung unter der Verwendung von temperaturabhängigen Matrixeigenschaften prognostiziert wurden. Informationen zum Anpassen des Werts von Rc finden Sie im Thema zu thermischen Restspannungen im Ansys-Benutzerhandbuch.
Bei einer aktuellen Temperatur T < Tamb stellt Gleichung 33 sicher, dass alle weiteren festgelegten Temperaturreduktionen nach Abkühlung die korrekten thermischen Spannungen erzeugen. In diesem Fall (T < Tamb) umfasst die gesamte Temperaturänderung ΔΤ, die von Helius PFA in Gleichung 32 verwendet wird, 50 % (mit dem Vorgabewert für Rc) der Temperaturänderung von der spannungsfreien Temperatur Tsf zur Umgebungstemperatur Tamb. Sie umfasst außerdem 100 % der zusätzlichen Temperaturreduzierung von der Umgebungstemperatur Tamb auf die aktuelle Temperatur T. Wenn jedoch die aktuelle Temperatur T gleich der Umgebungstemperatur Tamb ist oder darüber liegt, macht die gesamte Temperaturänderung ΔT, die Helius PFA in Gleichung 32 verwendet, nur 50 % (mit dem Vorgabewert für Rc) der tatsächlichen Temperaturänderung von der spannungsfreien Temperatur Tsf zur aktuellen Temperatur T aus. Beachten Sie, dass diese Methode zur Berechnung von ΔT sicherstellt, dass die thermischen Restspannungen verschwinden, wenn das Material erneut auf die Aushärtungstemperatur Tcure erhitzt wird.
Beachten Sie, dass bei T = Tamb die Gleichung 33a auf dieselbe Gleichung reduziert.
Angegebene Umgebung
Wenn ein einzigartiger Satz von Materialeigenschaften in den Berechnungen bei Umgebungstemperatur verwendet wird, wird die Temperaturänderung in zwei Schritten berechnet. Erstens für die Änderung von der Aushärtungstemperatur zur Umgebungstemperatur (Schritt A) und zweitens von der Umgebungstemperatur zur aktuellen Temperatur (Schritt C). (Schritt B impliziert eine Änderung der Feuchtigkeit von der Aushärtungsumgebung zur Umgebungsumgebung.)
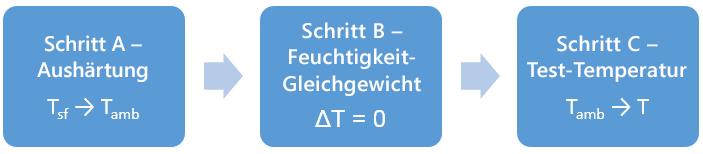
Für Schritt A werden die Materialeigenschaften bei Umgebungsfeuchtigkeit und -temperatur verwendet. Für Schritt A werden die Materialeigenschaften für die aktuelle Feuchtigkeit und Temperatur verwendet.

In der Gleichung 33b sind { } Macaulay-Klammern, wobei {x}=0 für x<0 und {x}=x für x ≥ 0 steht. Tamb ist die im Schlüsselwort *CURE STRESS in der HIN-Datei angegebene Umgebungstemperatur. Wenn keine Temperatur angegeben wird, ist Tamb entweder 72.5 °F, 22.5 °C oder 295.65 °K, je nach im Modell verwendeten Einheitensystem. T ist die Temperatur, bei der der Test durchgeführt wird (aktuelle Temperatur).
Die rechte Seite der Gleichung 33 stellt sicher, dass die thermischen Restspannungen am Ende der Abkühlung nach der Aushärtung auf Umgebungstemperatur (d. h., wenn T=Tamb) korrekt prognostiziert werden. Die Größe RcA gibt das Aushärtungsverhältnis für diesen Schritt an. Vorgabemäßig ist RcA auf einen Wert von 0.5 festgelegt. Dieser Vorgabewert basiert auf der Arbeit von Kenik [13]. Kenik hat gezeigt, dass eine einfache lineare elastische Analyse unter Verwendung von Verbundwerkstoff-Materialeigenschaften mit Raumtemperatur mit einer festgelegten Temperaturreduzierung um die Hälfte der tatsächlichen Abkühlung nach der Aushärtung thermische Restspannungen bei den Konstituenten ergibt, die ungefähr identisch sind mit den Spannungen, die mithilfe einer gründlicheren mikromechanischen Simulation der Abkühlung nach der Aushärtung unter der Verwendung von temperaturabhängigen Matrixeigenschaften prognostiziert wurden. Informationen zum Anpassen des Werts von RcA finden Sie im Thema zu thermischen Restspannungen im Ansys-Benutzerhandbuch.
Die rechte Seite der Gleichung 33c stellt sicher, dass alle weiteren festgelegten Temperaturreduktionen nach Abkühlung die korrekten thermischen Spannungen erzeugen. Beachten Sie, dass die Verwendung von Macaulay-Klammern { } sicherstellt, dass der erste Term auf der rechten Seite der Gleichung 33c nur zu ΔT beiträgt, wenn die aktuelle Temperatur T über der Umgebungstemperatur Tamb liegt. Die Größe RcC gibt das Aushärtungsverhältnis für diesen Schritt an. Vorgabemäßig ist RcC auf einen Wert von 0.5 festgelegt. Informationen zum Anpassen des Werts von RcC finden Sie im Thema Thermische Restspannungen im Ansys-Benutzerhandbuch. Wenn die aktuelle Temperatur T unter der Umgebungstemperatur Tambliegt, wird kein Aushärtungsverhältnis angewendet.
Die gesamte Temperaturänderung ΔΤ = ΔΤ Α + ΔΤ C.
MCT-Materialcharakterisierung von Verbundwerkstoffen
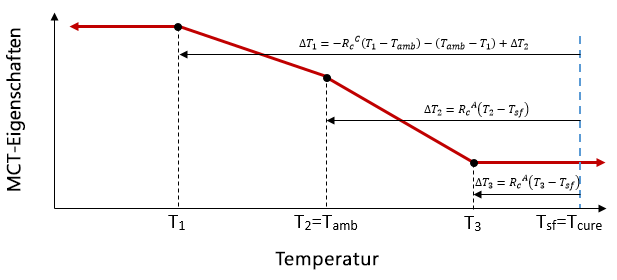
Die Gleichungen 32 und 33 werden auch während des MCT-Materialcharakterisierungsprozesses für Verbundmaterialien verwendet, die bei mehreren Temperaturen definiert werden. Die folgende Abbildung zeigt einen typischen Fall, in dem ein temperaturabhängiges Verbundmaterial bei drei verschiedenen Temperaturen T1, T2 und T3 charakterisiert wurde, wobei T1< Tamb, T2=Tamb und Tamb< T3< Tcure ist. Die Abbildung zeigt außerdem die Temperaturänderung ΔT (berechnet über die Gleichungen 33a-c), die in der mikromechanischen Analyse des Verbundmaterials bei jeder der drei Temperaturen während des MCT-Charakterisierungsprozesses eingeschlossen ist. Bei der Charakterisierung haben diese festgelegten Temperaturänderungen Einfluss auf die Bestimmung der Konstituentenausfallkoeffizienten. Wenn beispielsweise das mikromechanische Modell mechanisch bis zu einem gemessenen Ausfalllastniveau belastet wird, enthält der Ausfallspannungszustand in den Konstituentenmaterialien Anteile der mechanischen Last und der festgelegten Temperaturänderung.
Aktuelle Umgebung:
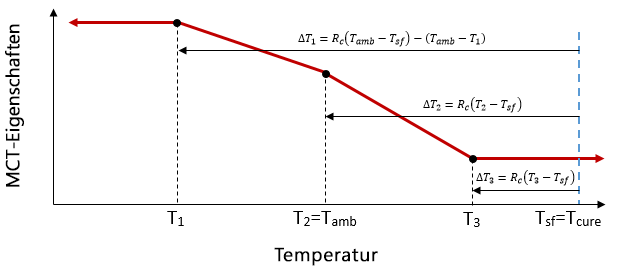
Angegebene Umgebung: