Schadenszustände in unidirektionalen Verbundmaterialien
Für unidirektionale Verbundmaterialien gibt es drei Verbundschadenszustände.
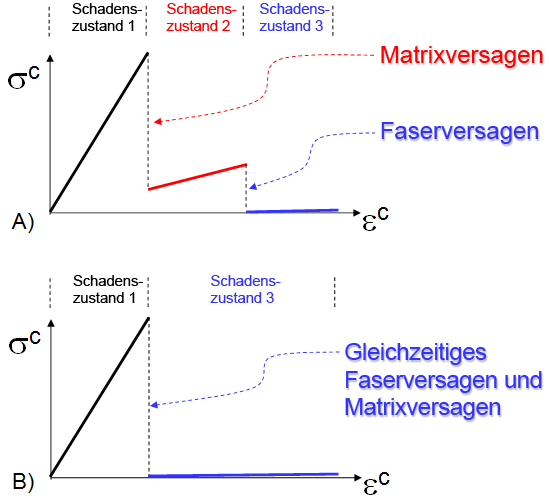
Schadenszustand 1: nicht ausgefallene Matrixkonstituente und nicht ausgefallene Faserkonstituente
Schadenszustand 2: ausgefallene Matrixkonstituente und nicht ausgefallene Faserkonstituente
Schadenszustand 3: ausgefallene Matrixkonstituente und ausgefallene Faserkonstituente
Theoretisch wäre auch ein vierter Verbundschadenszustand möglich: eine nicht ausgefallene Matrixkonstituente in Kombination mit einer ausgefallenen Faserkonstituente. Praktisch ist es bei den meisten faserverstärkten Verbundmaterialien jedoch unmöglich, Lasten anzuwenden, die einen Faserfehler verursachen, ohne auch einen Matrix-Fehler zu bewirken. Daher wird davon ausgegangen, dass – unabhängig von der genauen Form der auf das Verbundmaterial einwirkenden kombinierten Last – eine gleichmäßige Erhöhung der Größe der Last einen der beiden möglichen Verläufe des Schadenszustands des VerbundmaterialsCIR bewirkt.
Verlauf 1: Schadenszustand 1 → Schadenszustand 2 → Schadenszustand 3
Verlauf 2:Schadenszustand 1 → Schadenszustand 3
Die folgende Abbildung veranschaulicht diese beiden Verläufe qualitativ. Bezüglich der Gesamtreaktion des Verbundmaterials (siehe Abbildung unten) sollten mehrere Punkte näher betrachtet werden. Zunächst werden für jeden der drei individuellen Schadenszustände des Verbundmaterials dessen Steifheits- und thermischen Eigenschaften (Cc und αc) durch Homogenisierung der Mikrostruktur ermittelt, deren Konstituentenmaterialien jeweils den Zustand "Ausgefallen" oder "Nicht ausgefallen" aufweisen. Bei einer ausgefallenen Matrixkonstituente in der Mikrostruktur wird deren Steifheit isotropisch auf einen benutzerdefinierten Prozentsatz (Vorgabe = 10 %) der ursprünglichen MatrixsteifheitCIR reduziert. Diese reduzierte Matrixsteifheit wirkt sich über die Homogenisierung direkt auf die Steifheit des Verbundmaterials aus. Bei einer ausgefallenen Faserkonstituente in der Mikrostruktur wird deren Steifheit isotropisch auf einen benutzerdefinierten Prozentsatz (Vorgabe = 1 %) der ursprünglichen MatrixsteifheitCIR reduziert. Diese reduzierte Fasersteifheit wirkt sich über die Homogenisierung direkt auf die Steifheit des Verbundmaterials aus.
Des Weiteren muss für jeden der drei unten gezeigten Verbundschadenszustände eine separate MCT-Zerlegung formuliert werden. Vergessen Sie nicht, dass die MCT-Zerlegung lineare Konstitutivbeziehungen erfordert, in denen die einzelnen Komponenten Cc, Cf, Cm, αc, αf und αm einfache Konstanten sind. Im Allgemeinen unterscheiden sich diese Konstanten zwischen einem linearen Segment der Reaktion und dem anderen, sodass auch die MCT-Zerlegung in jedem Abschnitt unterschiedlich ausfällt. Durch Beschränkung der gesamten Reaktion des Verbundmaterials auf drei Schadenszustände muss der Vorgang zur Ermittlung der MCT-Zerlegungskonstanten, die für jedes Segment der Reaktion benötigt werden, nur einmal durchgeführt werden. Die resultierenden Konstanten werden in einer Datenbank gespeichert. Anschließend kann je nach einzelnem Schadenszustand des Verbundmaterials der entsprechende Satz von MCT-Zerlegungskonstanten einfach aus der Datenbank abgerufen werden. Diese Funktion trägt erheblich zur gesamten Berechnungseffizienz von Helius PFA bei.
Schließlich sollte hervorgehoben werden, dass bei der progressiven Fehleranalyse von großen Verbundstrukturen die Verwendung von deutlich separaten Materialreaktionen (wie unten dargestellt) nicht unbedingt zu ähnlich deutlich separaten Reaktionen der Gesamtverbundstruktur führen muss. Im Gegenteil, die prognostizierte progressive Ausfallsreaktion der Verbundstruktur verläuft bis zur endgültigen Ausfallslast oft sehr gleichmäßig. Der Grund für dieses nicht intuitive Ergebnis ist, dass die separate Materialreaktion (siehe unten) unabhängig auf Tausende (oder Millionen) von Gaußschen Integrationspunkten angewendet wird, die über die gesamte Struktur verteilt sind. Wenn das Spannungsniveau in der Struktur von Punkt zu Punkt variiert, kann davon ausgegangen werden, dass es bei einem Lastinkrement nur in einem sehr geringen Prozentsatz dieser Gaußschen Integrationspunkte zu einem Ausfall kommt. Daher reagiert die Struktur trotz der nicht kontinuierlichen Konstitutivbeziehungen gleichmäßig.