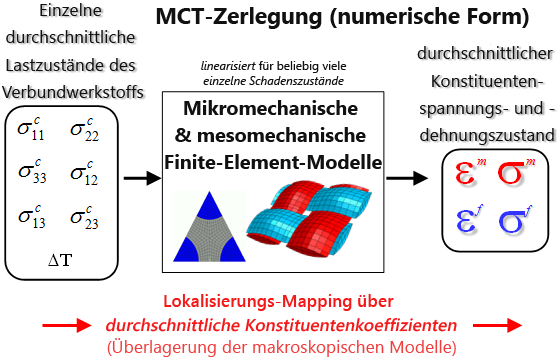
Numerische Form der MCT-Zerlegung
Eine Darstellung der numerischen Zerlegung basierend auf der Verwendung von Finite-Element-Modellen des Verbundmaterials.
Verbundmaterialien sind häufig komplexer als ein einfaches unidirektionales faserverstärktes Material, das nur Faser- und Matrixkonstituenten umfasst. Beispiel: Gewebte und geflochtene Verbundmaterialien enthalten eine Mesostruktur bestehend aus zwei oder mehr Gruppen von Garnen und reinen Matrixtaschen (d. h. Mesokonstituenten). Die Mesokonstituenten ihrerseits bestehen aus Mikrokonstituenten (Fasern und Matrix). In diesem Fall müssen die Durchschnittszustände für Spannung und Dehnung des gewebten Verbundmaterials in die entsprechenden Durchschnittszustände für Spannung und Dehnung der Mesokonstituenten zerlegt werden. Anschließend müssen die Durchschnittszustände für Spannung und Dehnung der Mesokonstituenten weiter in die Durchschnittszustände für Spannung und Dehnung der Mikrokonstituenten (Fasern und Matrix) zerlegt werden. Helius PFA führt die endgültige Zerlegung unter Verwendung der zuvor beschriebenen binären analytischen Zerlegung durch (Analytische Form der MCT-Zerlegung). Die binäre analytische Zerlegung eignet sich nicht für die erste Zerlegung (von Durchschnittswerten für den Verbund in Durchschnittswerte für die Mesokonstituenten), da es mehr als zwei Mesokonstituenten gibt. Dasselbe gilt auch für den Fall eines Verbundmaterials mit mehr als zwei Mikrokonstituenten. Für Zerlegungen in drei oder mehr Mesokonstituenten bzw. Mikrokonstituenten verwendet Helius PFA einen numerische Zerlegung basierend auf der Verwendung von Finite-Element-Modellen der Meso- oder Mikrostruktur des Verbundmaterials.
Die Abbildung unten zeigt eine schematische Darstellung der numerischen Zerlegungsmethode, die auf hochgenauen Finite-Element-Modellen der Meso- und Mikrostruktur des Verbundmaterials beruht. Diese numerische Methode würde beispielsweise für ein Leinwandbindungs-Verbundmaterial die Verwendung eines mesoskalierten Finite-Element-Modells des gewebten Verbundmaterials erfordern, dem eine homogenisierte Materialbeschreibung der Kettgarne, Schussgarne und Matrixtaschen zugrunde liegt, d. h. ein Finite-Element-Modell mit drei Mesokonstituenten. In das mesoskalierte Finite-Element-Modell können einzelne homogene makroskopische Spannungszustände eingeführt werden, und die resultierende Lösung kann zur Berechnung der durchschnittlichen Spannungs- und Dehnungszustände in den homogenisierten Kettgarnen, Schussgarnen und reinen Matrixtaschen verwendet werden. Diese mesoskalierte Finite Element Lösung kann auch zur Berechnung von Sätzen von Einflusskoeffizienten verwendet werden, die direkt makroskopische Spannung- und Dehnungskomponenten in durchschnittliche Spannungs- und Dehnungszustände der Mesokonstituenten (Kettgarne, Schussgarne und Matrixtaschen) abbilden. Dabei wird für jeden diskreten Schadenszustand, den das gewebte Verbundmaterial aufweisen kann, jeweils ein Satz dieser Einflusskoeffizienten ermittelt. Die resultierenden Koeffizienten werden in einer Materialdatenbank für den sofortigen Zugriff während einer progressiven Versagenssimulation auf Strukturebene gespeichert. Die durchschnittlichen Spannungs- und Dehnungszustände in den homogenisierten Kett- und Schussgarnen können mithilfe der binären analytischen Zerlegung in durchschnittliche Spannungs- und Dehnungszustände von Fasern und Matrix zerlegt werden.