Entwicklung von gewebte Mikrostrukturen
Prüfen Sie die Details von Geometrie, Mikrostruktur und Einschränkungen für Gewebematerialien.
Geometrieerzeugung
Derzeit unterstützt Composite Material Manager fünf Arten von Mikrostrukturen. Die erste und einfachste ist der unidirektionale Verbundwerkstoff, der sich aus in einem Matrixmaterial eingebetteten Fasern zusammensetzt. Die vier übrigen bestehen aus zweidimensionalen gewebten Mikrostrukturen. Diese umfassen normale gewebte, 4-bindige, 5-bindige und 8-bindige Verbundwerkstoffe.
Für jede Mikrostruktur sind geometrische Parameter erforderlich, um ein realistisches Modell zu erstellen. Im Fall eines unidirektionalen Materials ist nur der Faservolumenanteil (FVF) des unidirektionalen Verbundmaterials erforderlich. Mithilfe des FVF und unter Annahme einer sechseckigen Faserpaketanordnung wird die Geometrie eines Mikromechanikmodells für den gewünschten Verbundwerkstoff entwickelt. Allerdings ist die Geometrie gewebter Stoffe aus zwei Gründen deutlich komplexer:
- Viele Parameter sind erforderlich, um die Geometrie der Einheitenzelle zu beschreiben.
- Es wird kein universeller Datensatz verwendet, um die Geometrie eines normalen Gewebes zu beschreiben.
Zweidimensionale gewebte Materialien kommen in einer Vielzahl von Kombinationen vor, wie z. B. symmetrische Leinwand-, unsymmetrische Leinwand-, Köper- und Atlasbindungen. Die aktuellen Modelle, die in Helius PFA verwendet werden, sind zweidimensional Leinwand- und 4-, 5- und 8-bindig gewebte Mikrostrukturen. Für andere gewebte Konfigurationen, die nur orthogonale Garne enthalten, wie z. B. Köperbindung, bietet das Leinwandbindungsmodell eine sinnvolle Abschätzung. Es bleibt jedoch Ihnen überlassen, die Genauigkeit der Ergebnisse zu bestimmen. Daher wird empfohlen, dass Sie eine Obergrenze für die Lagenmaterialeigenschaften berechnen, indem Sie das Material als lageübergreifende unidirektionale Lage modellieren (wobei jede Lage eine bestimmte Garnrichtung darstellt). Für Mikrostrukturen mit nicht orthogonalen Garnen, z. B. dreiaxiale Flechtungen, bietet Autodesk derzeit keine Funktionen für die Modellierung.
Die folgenden Abschnitte beschreiben die Mikrostruktur gewebter Stoffe, die mit Helius PFA implementiert wurden, und geben Einblick in die Auswahl der erforderlichen Parameter, um Ihre gewebten Materialien korrekt zu charakterisieren.
Normale gewebte Mikrostruktur
Das Mikromechanikmodell für normale Gewebe besteht aus Schussgarnen, Kettgarnen und einer Matrixtasche. Bei den Schuss- und Kettgarnen wird davon ausgegangen, dass sie lotrecht zueinander verlaufen. Die Einheitenzelle, die als Modell für diesen Mikrostrukturtyp ausgewählt wurde, wurde von Kuhn und Charalambides [1] übernommen und wird unten gezeigt.
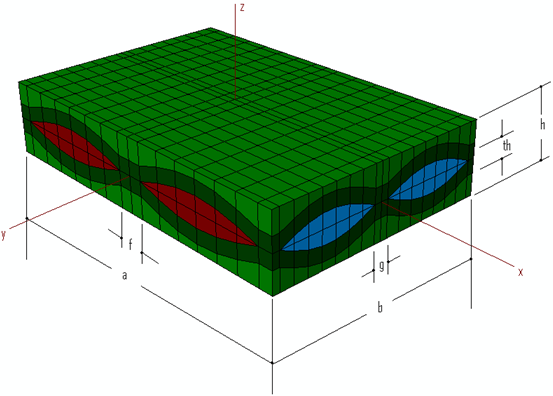
Wie oben dargestellt, gibt es viele Parameter, die erforderlich sind, um die Geometrie der Einheitenzelle vollständig zu beschreiben. Zu diesen gehören:
- Die Länge der Einheitenzelle
- Die Breite der Einheitenzelle
- Die Höhe der gesamten Einheitenzelle
- Die Höhe der Schussgarne
- Die Höhe der Kettgarne
- Der Abstand zwischen den Schussgarnen
- Der Abstand zwischen den Kettgarnen
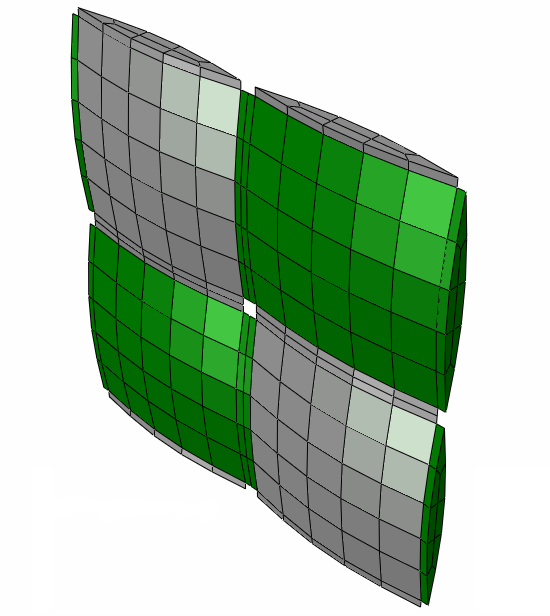
Eine Ansicht der Einheitenzelle ohne Matrixtasche wird unten gezeigt.
Reduzierte Einheitenzellmikrostruktur (Atlasbindungen)
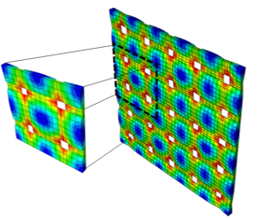
Die reduzierte Einheitenzellmikrostruktur (RUC-Mikrostruktur) für Atlasbindungen ist eine Adaptation der vollständigen Einheitenzellmikrostruktur. Die RUC-Mikrostruktur ist einfach eine Teilmenge der sich wiederholenden Geometrie in der FUC-Mikrostruktur. Anstatt die Mikrostruktur für jedes n-bindige Material anzupassen, behält die RUC eine konstante Größe und Topologie bei. Nur die Amplitude der Krümmung der beiden mittleren Garnen wird angepasst, wenn sich die Bindungszahl ändert.

 -
-
Die Amplitude wird insbesondere angepasst, damit die durchschnittliche Steifheit in der Ebene (E11, E22, G12) mit den experimentell beobachteten Werten für jede Bindungszahl übereinstimmt.
Die RUC-Mikrostruktur hat den Vorteil, dass sie kleiner ist als die FUC und daher viel schneller charakterisiert werden kann. Als Ergebnis unterstützt die RUC-Mikrostruktur die direkte Degradation der Faser- und Matrixsteifheiten. Sie unterstützt darüber hinaus Nichtlinearität vor Ausfall, die nicht für die FUC unterstützt wird.
Einschränkungen experimenteller Daten
Experimentelle Daten für faserverstärkte gewebte Verbundmaterialien weisen in der Regel nur den Faservolumenanteil für den gesamten Verbundwerkstoff auf. Wie bei faserverstärkten unidirektionalen Verbundmaterialien ist dies ein Maß des Gesamtvolumens, das die Fasern innerhalb des Verbundwerkstoffs relativ zum Gesamtvolumen des Verbundwerkstoffs einnehmen. Zwar funktioniert dies gut bei unidirektionalen Materialien, es wird jedoch nicht die Geometrie der gewebten Mikrostruktur erfasst. Eine wichtige Frage muss beantwortet werden, um die Geometrie der Einheitenzelle mit den oben beschriebenen Parametern zu verknüpfen. Welche Volumenanteile haben die Schuss- und Kettgarne?
Zur Beantwortung dieser Frage müssen wir zunächst die Beziehungen zwischen Volumenanteilen erarbeiten. Der Gesamtfaservolumenanteil des Verbundmaterials kann in Bezug auf die Volumenanteile der Schuss- und Kettgarne sowie der entsprechenden Faservolumenanteile beschrieben werden, und zwar als
FVF = BVFFill (FVFFill ) + BVFWarp (FVFWarp ) , (Gleichung 1)
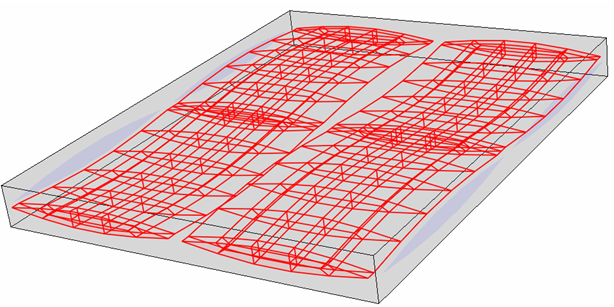
Hierbei ist BVFFill der Volumenanteil des Schusspakets, BVFWarp der Volumenanteil des Kettpakets, FVFFill der Faservolumenanteil des Schussgarns und FVFWarp der Faservolumenanteil des Kettgarns. Ein Paketvolumenanteil wird definiert als Bruchteil des Volumens, den das angegebene Garn im Vergleich zum gesamten Verbundwerkstoff belegt. Eine detailliertere Beschreibung des Paketvolumenanteils und seine Bedeutung im Kontext der Geometrie der normalen Gewebeeinheitenzelle gibt die Abbildung unten. Der rot markierte Bereich stellt das Volumen dar, das die Schussgarne in der gesamten Verbund-Einheitenzelle belegen. Der Schusspaketvolumenanteil wird als Volumen der Schussgarne geteilt durch das Volumen des Verbundwerkstoffs berechnet.
Annahmen
Zunächst ein paar Annahmen zur Geometrie der Einheitenzelle. Zuerst gehen wir davon aus, dass der Schuss- und der Kettgarn gleich hoch sind, wodurch die Abhängigkeit von beiden Höhen eliminiert wird. Die zweite Annahme legt fest, dass die Gesamthöhe der Einheitenzelle und die Höhe der Garne für jede Geometriespezifikation konstant sind. Dadurch entfällt praktisch die dritte, vierte und fünfte Abhängigkeit in der Liste oben.
Schließlich gehen wir davon aus, dass die Breite der Garne gleich und konstant ist. Deshalb können Breite und Länge der Einheitenzelle zum Abstand der Garne wie folgt in Beziehung gesetzt werden:
a = Breite + 2f
b = Breite + 2g , (Gleichung 2)
Deshalb sind nur zwei unbekannte Parameter erforderlich, um die Geometrie der Einheitenzelle vollständig zu beschreiben; der Abstand zwischen den Schussgarnen und der Abstand zwischen den Kettgarnen. Diese Parameter stehen in direkter Beziehung zu den Volumenanteilen der Schuss- und Kettpakete sowie zur Anzahl der Wellenformen pro Längeneinheit. Composite Material Manager verwendet Paketvolumenanteile (BVFs) zum Definieren der Mikrostruktur.
Es wird davon ausgegangen, dass die Faservolumenanteile der Schuss- und Kettpakete gleich sind, wodurch sich Gleichung 1 wie folgt reduziert:
FVF = (BVFFill + BVFWarp )FVFTow , (Gleichung 3)