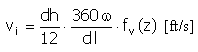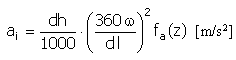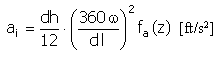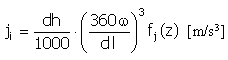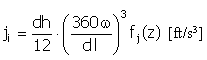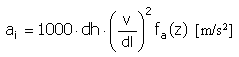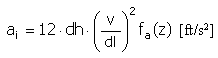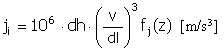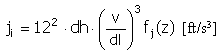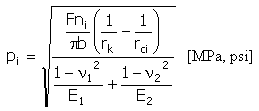Eingangswerte:
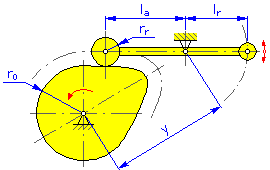
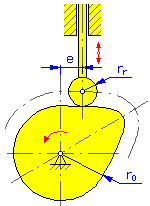
- Grundradius r 0 (Kurvenscheiben und zylindrische Nocken)
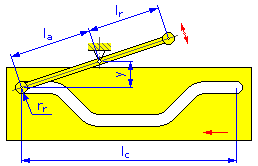
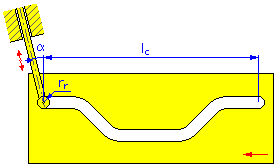
- Länge der Bewegung l c (lineare Nocken)
- Nockenbreite b c
- Rollenradius r r
- Rollenbreite b r (für zylindrische Stößelformen)
- Exzentrizität e (Kurvenscheiben für Übersetzungsstößel)
- Exzentrizitätswinkel α (lineare und zylindrische Nocken für Übersetzungsstößel)
- Drehpunktabstand y (Kurvenscheiben und lineare Nocken für Schwungarm)
- Armlänge l a (Kurvenscheiben und lineare Nocken für Schwungarm)
- Reaktionsarm l r (Kurvenscheiben und lineare Nocken für Schwungarm)
- Drehzahl ω (Kurvenscheiben und zylindrische Nocken)
- Geschwindigkeit v (lineare Nocken)
- Kraft an Rolle F
- Gewicht der zu hebenden Teile m
- Federrate c
- Zulässiger Druck p A1
- Elastizitätsmodul des Nockenmaterials E 1
- Poissonsche Konstante des Nockenmaterials μ 1
- Zulässiger Druck p A2
- Elastizitätsmodul des Stößelmaterials E 2
- Poissonsche Konstante des Stößelmaterials μ 2
|
Kurvenscheibe |
|
|
|
|
|
Linearer Nocken |
|
|
|
|
|
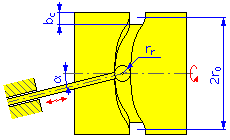
Zylindrischer Nocken |
|
 |
|
|
Außendurchmesser = 2r 0 + b c |
|
|
Innendurchmesser = 2r 0 - b c |
|
Nockensegmente
- Bewegungsfunktion f y (z) [ul]
- Umgekehrtes Verhältnis k r (nur für die Bewegungen Parabel und Parabel mit linearem Teil)
- Lineares Teileverhältnis k l (nur für die Bewegung Parabel mit linearem Teil)
- Anfangsposition der Nocke l 0 [°; mm, in]
- Endposition der Bewegung l [°; mm, in]
- Länge der Bewegung für Segment dl = l - l 0 [°; mm, in]
- Hub am Anfang h 0 [mm, in]
- Hub am Ende h max [mm, in]
- Segmenthub d h = h max - h 0 [mm, in]
Hubabhängigkeiten
Kurvenscheibe und zylindrischer Nocken
Drehwinkel des Nockens ϕ i [°]
Tatsächliche relative Position im Segment: z i = (ϕ i - l 0 ) / dl (Bereich 0 - 1)
|
Hub |
y i = dh f y (z) [mm, in] |
|
Drehzahl |
|
|
|
|
|
Beschleunigung |
|
|
|
|
|
Puls |
|
|
|
Linearer Nocken
Nockenbewegungsposition l i [mm, in]
Tatsächliche relative Position im Segment: z i = (l i - l 0 ) / dl (Bereich 0 - 1)
|
Hub |
y i = dh f y (z) [mm, in] |
|
Drehzahl |
|
|
Beschleunigung |
|
|
|
|
|
Puls |
|
|
|
Bewegungsfunktionen
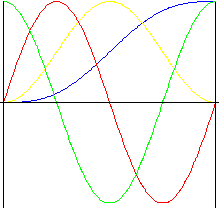
Zykloide (verlängerte Sinuslinie)
Diese Bewegung verfügt über exzellente Beschleunigungseigenschaften. Sie wird häufig für Hochgeschwindigkeitswellen verwendet, da sie zu geringer Geräuschentwicklung, geringen Vibrationen und geringem Verschleiß führt.
|
|
Hub |
|
|
Drehzahl |
|
|
Beschleunigung |
|
|
Puls |
|
Hub |
f y (z) = z - 0.5/π sin(2πz) |
|
Drehzahl |
f v (z) = 1 - cos (2πz) |
|
Beschleunigung |
f a (z) = 2π sin(2πz) |
|
Puls |
f j (z) = 4π 2 cos(2πz) |
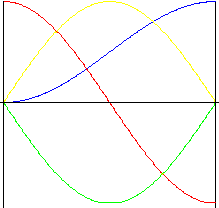
Harmonisch (Sinuslinie)
Kontinuierliche Geschwindigkeit und Beschleunigung während des Hubs ist der inhärente Vorteil dieser Kurve. Die direkten Beschleunigungsänderungen am Anfang und Ende der Bewegung führen jedoch u. U. zu Vibrationen, Geräuschentwicklung und Verschleiß.
|
|
Hub |
|
|
Drehzahl |
|
|
Beschleunigung |
|
|
Puls |
|
Hub |
f y (z) = 0.5 (1 - cos πz)) |
|
Drehzahl |
f v (z) = 0.5 π sin (πz) |
|
Beschleunigung |
f a (z) = 0.5 π 2 cos(πz) |
|
Puls |
f j (z) = -0.5π 3 sin(πz) |
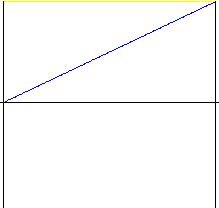
Linear
Einfache Bewegung mit einem erheblichen Stoß am Anfang und Ende. Selten verwendet, es sei denn in sehr einfachen Vorrichtungen. Wir empfehlen die Verwendung von Bewegungen mit modifizierten Anfangs- und Endphasen - parabolisch mit linearem Teil.
|
|
Hub |
|
|
Drehzahl |
|
Hub |
f y (z) = z |
|
Drehzahl |
f v (z) = 1 |
|
Beschleunigung |
f a (z) = 0 |
|
Anmerkung: Für z = 0 und z = 1 sollte der korrekte Wert unbegrenzt sein; die Berechnung ist mit einem unbegrenzten Wert jedoch nicht möglich, daher wird ein Nullwert verwendet.
|
|
|
Puls |
f j (z) = 0 |
|
Anmerkung: Für z = 0 und z = 1 sollte der korrekte Wert unbegrenzt sein; die Berechnung ist mit einem unbegrenzten Wert jedoch nicht möglich, daher wird ein Nullwert verwendet.
|
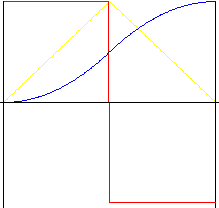
Parabolisch (Polynom 2.Grades)
Bewegung mit der geringstmöglichen Beschleunigung Aufgrund der plötzlichen Beschleunigungsänderung zu Anfang, in der Mitte und am Ende der Bewegung kommt es jedoch zu Stößen. Ein umgekehrtes Verhältnis ermöglicht jedoch das "Ausdehnen" der Bewegungsmitte zur Veränderung des positiven und negativen Beschleunigungsverhältnisses.
Symmetrisch (Umkehrverhältnis k r = 0.5)
|
|
Hub |
|
|
Drehzahl |
|
|
Beschleunigung |
|
für z = 0 to 0.5: |
|||
|
Hub |
fy(z) = 2z 2 |
||
|
Drehzahl |
fv(z) = 4z |
||
|
Beschleunigung |
fa (z) = 4 |
||
|
Puls |
fa(z) = 0 |
||
|
für z = 0.5 - 1: |
|||
|
Hub |
fy(z) = 1 - 2(1 - z) 2 |
||
|
Drehzahl |
fv(z) = 4 (1 - z) |
||
|
Beschleunigung |
fa (z) = -4 |
||
|
Puls |
fj(z) = 0 |
||
|
Anmerkung: Für z = 0 und z = 1 sollte der korrekte Wert unbegrenzt sein; die Berechnung ist mit einem unbegrenzten Wert jedoch nicht möglich, daher wird ein Nullwert verwendet.
|
|||
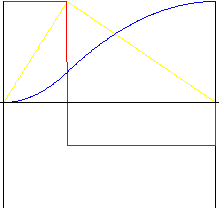
Asymmetrisch
k r - Umkehrverhältnis (im Bereich 0.01 bis 0.99)
|
|
Hub |
|
|
Drehzahl |
|
|
Beschleunigung |
|
für z = 0 bis k r : |
|||
|
Hub |
f y (z) = z 2 / k r |
||
|
Drehzahl |
f v (z) = 2z / k r |
||
|
Beschleunigung |
f a (z) = 2 / k r |
||
|
Puls |
f j (z) = 0 |
||
|
für z = k r bis 1: |
|||
|
Hub |
f y (z) = 1 – (1 – z) 2 / (1 – k r ) |
||
|
Drehzahl |
f v (z) = 2 (1 – z) / (1 – k r ) |
||
|
Beschleunigung |
f a (z) = -2 / (1 - k r ) |
||
|
Puls |
f j (z) = 0 |
||
|
Anmerkung: Für z = 0 und z = 1 sollte der korrekte Wert unbegrenzt sein; die Berechnung ist mit einem unbegrenzten Wert jedoch nicht möglich, daher wird ein Nullwert verwendet.
|
|||
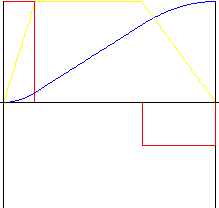
Parabel mit linearem Teil
Bessere positive und negative Beschleunigung als bei linearer Bewegung. Ein umgekehrtes Verhältnis ermöglicht jedoch das "Ausdehnen" der Bewegungsmitte zur Veränderung des positiven und negativen Beschleunigungsverhältnisses. Das Verhältnis im linearen Teil ermöglicht das Definieren der relativen Größe des linearen Bewegungsteils.
|
|
Drehzahl |
|
|
Beschleunigung |
|
|
Puls |
k r - Umkehrverhältnis (im Bereich 0.01 bis 0.99)
k l - Verhältnis im linearen Teil (im Bereich 0 bis 0.99)
k z = 1 + k l / (1 - k l )
k h = (1 - k l ) / (1 + k l )
|
für z = 0 bis k r / k z : |
|||
|
Hub |
f y (z) = k h z 2 k z 2 / k r |
||
|
Drehzahl |
f v (z) = 2 k h z k z 2 / k r |
||
|
Beschleunigung |
f a (z) = 2 k h k z 2 / k r |
||
|
Puls |
f j (z) = 0 |
||
|
für z = k r / k z bis r / k z + k l : |
|||
|
Hub |
f y (z) = (z - 0.5 k r / k z ) 2 / (1 + k l ) |
||
|
Drehzahl |
f v (z) = 2 / (1 + k l ) |
||
|
Beschleunigung |
f a (z) = 0 |
||
|
Puls |
f j (z) = 0 |
||
|
für z = k r / k z + k l bis 1: |
|||
|
Hub |
f y (z) = 1 - k h (1 - z) 2 k z 2 / (1 - k r ) |
||
|
Drehzahl |
f v (z) = 2 k h (1 - z) k z 2 / (1 - k r ) |
||
|
Beschleunigung |
f a (z) = -2 k h k z 2 / (1 - k r ) |
||
|
Puls |
f j (z) = 0 |
||
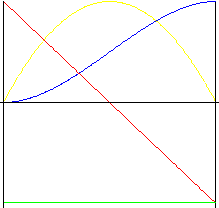
Polynom 3.Grades (kubische Parabel)
Bewegung mit geringeren Stößen als bei parabolischer Bewegung
|
|
Hub |
|
|
Drehzahl |
|
|
Beschleunigung |
|
|
Puls |
|
Hub |
f y (z) = (3 -2z) z 2 |
|
Drehzahl |
f v (z) = (6 - 6z) z |
|
Beschleunigung |
f a (z) = 6 - 12z |
|
Puls |
f j (z) = -12 |
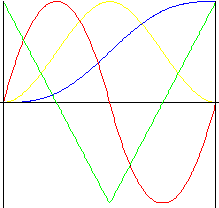
Polynom 4.Grades
Bewegung mit geringeren Stößen als bei Polynom 3.Grades
|
|
Hub |
|
|
Drehzahl |
|
|
Beschleunigung |
|
|
Puls |
|
für z = 0 - 0.5 |
||
|
Hub |
f y (z) = (1 - z) 8z 3 |
|
|
Drehzahl |
f v (z) = (24 - 32z) z 2 |
|
|
Beschleunigung |
f a (z) = (48 - 96z) z |
|
|
Puls |
f j (z) = 48 - 192z |
|
|
für z = 0,5 -1 |
||
|
Hub |
f y (z) = 1 - 8z (1 - z) 3 |
|
|
Drehzahl |
f v (z) = (32z - 8) (1 - z) 2 |
|
|
Beschleunigung |
f a (z) = (48 - 96z) (1 - z) |
|
|
Puls |
f j (z) = 194z - 144 |
|
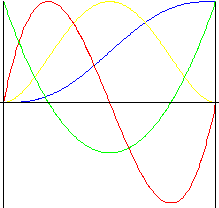
Polynom 5.Grades
Bewegung mit geringeren Stößen als bei Polynom 3.Grades
|
|
Hub |
|
|
Drehzahl |
|
|
Beschleunigung |
|
|
Puls |
|
Hub |
f y (z) = (6z 2 - 15z + 10) z 3 |
|
Drehzahl |
f v (z) = (z 2 - 2z + 1) 30z 2 |
|
Beschleunigung |
f a (z) = (2z 2 - 3z + 1) 60z |
|
Puls |
f j (z) = (6z 2 - 6z + 1) 60 |
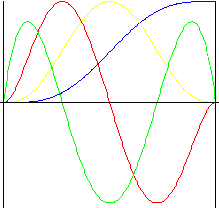
Polynom 7.Grades
Stetigkeit in allen Formeln, einschließlich Impuls
|
|
Hub |
|
|
Drehzahl |
|
|
Beschleunigung |
|
|
Puls |
|
Hub |
f y (z) = (-20z 3 + 70z 2 - 84z + 35) z 4 |
|
Drehzahl |
f v (z) = (-z 3 + 3z 2 - 3z + 1) 140z 3 |
|
Beschleunigung |
f a (z) = (-2z 3 + 5z 2 - 4z + 1) 420z 2 |
|
Puls |
f j (z) = (-5z 3 + 10z 2 - 6z + 1) 840z |
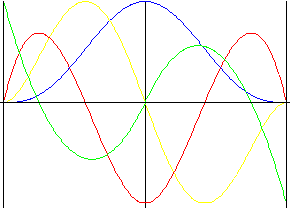
Asymmetrisches Polynom 5.Grades
Ähnlich wie Polynom 5. Grades, jedoch mit erzwungener Hubumkehr.
|
|
Hub |
|
|
Drehzahl |
|
|
Beschleunigung |
|
|
Puls |
|
Bauteil 1 |
||
|
Hub |
f y (z) = 1 - (8 (1 - z) 3 - 15 (1 - z) 2 + 10) (1 - z) 2 / 3 |
|
|
Drehzahl |
f v (z) = (2 (1 - z) 3 - 3 (1 - z) 2 + 1) (1 - z) 20 / 3 |
|
|
Beschleunigung |
f a (z) = -(8 (1 - z) 3 - 9 (1 - z) 2 + 1) 20 / 3 |
|
|
Puls |
f j (z) = (4 (1 - z) 2 - 3 (1 - z)) 40 |
|
|
Bauteil 2 |
||
|
Hub |
f y (z) = (8z 3 - 15z 2 + 10) z 2 / 3 |
|
|
Drehzahl |
f v (z) = (2z 3 - 3z 2 + 1) z 20/3 |
|
|
Beschleunigung |
f a (z) = (8z 3 - 9z 2 + 1) 20/3 |
|
|
Puls |
f j (z) = (4z 2 - 3z) 40 |
|
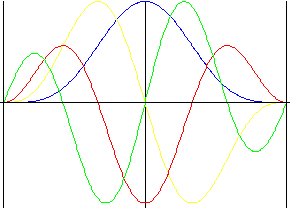
Doppeltharmonisch
Stetigkeit in allen Formeln, einschließlich Impuls mit erzwungener Hubumkehr.
|
Bauteil 1 |
||
|
Hub |
f y (z) = cos(0.5π (1 - z)) 4 |
|
|
Drehzahl |
f v (z) = π (0.5 sin(πz) - 0.25 sin(2πz)) |
|
|
Beschleunigung |
f a (z) = 0.5 π 2 (cos(πz) - cos(2πz)) |
|
|
Puls |
f j (z) = π 3 (-0.5 sin(πz) + sin(2πz)) |
|
|
Bauteil 2 |
||
|
Hub |
f y (z) = 1 - cos(0.5π z) 4 |
|
|
Drehzahl |
f v (z) = π (0.5 sin(πz) + 0.25 sin(2πz)) |
|
|
Beschleunigung |
f a (z) = 0.5 π 2 (cos(πz) + cos(2πz)) |
|
|
Puls |
f j (z) = -π 3 (0.5 sin(πz) + sin(2πz)) |
|
Vergleich der maximalen relativen Werte
|
Bewegung |
Drehzahl |
Beschleunigung |
Puls |
|
Zykloide (verlängerte Sinuslinie) |
2 |
6.28 |
39.5 |
|
Harmonisch (Sinuslinie) |
1.57 |
4.93 |
15.5 |
|
Linear |
1 |
∞ |
∞ |
|
Parabolisch (Polynom 2.Grades) |
2 |
4 |
∞ |
|
Polynom 3.Grades |
1,5 |
6 |
12 |
|
Polynom 4. Grades |
2 |
6 |
48 |
|
Polynom 5. Grades |
1.88 |
5.77 |
60 |
|
Polynom 7. Grades |
2.19 |
7.51 |
52.5 |
|
Asymmetrisches Polynom 5. Grades |
1.73 |
6.67 |
40 |
|
Doppeltharmonisch |
2.04 |
9.87 |
42.4 |
Andere Abhängigkeiten
Kraft an Rolle
|
F i = F + m a i + c y i [N, lb] |
Normalkraft
|
Fn i = F i / cos (γ i ) [N, lb] |
Drehmoment
|
T i = F i r i tan (γ i ) [Nmm, lb in] |
Spezifischer Druck (nach Hertz)
|
|
|
|
b = min (b v, b k ) |