Circle
Circle
Creates a NURBS curve in the form of a planar circle.
Access this tool from the Curves tool palette:

Circle Options
Periodic Circle
When this option is turned on (check mark) the circles are closed curves, with the first and last span overlapping. (The result corresponds to the circle primitives created in previous versions of the software.)
When this option is turned off (no check mark), the circles are open curves, with only the first and last CV touching. They can be opened by moving those CVs apart. They also use an algorithm that produces better quality circles and the ability to specify a range of degrees (see the following options).
The following options only appear when Periodic is turned on.
Degree
The degree of the NURBS curve. The values range from 1 to 7. The default is 5.
Spans
The number of subdivisions (spans) on the curve.
The default is 12. A workable primitive shape usually has at least 4 subdivisions. It is not usually necessary to use more than 20 subdivisions.
The following options only appear when Periodic is turned off.
Sweep Angle
The degrees of rotation around the center of the circle.
For example, if you enter 180 degrees, Alias creates a half circle.
Segments
Specifies the number of curve segments in the circle.
Degree
Specifies the degree of the circle. The values range from 2 to 7. The default is 5.
Spans
Specifies the number of spans in the circle. The values range from 1 to 14. The default is 1.
About rational and non-rational geometry
Non-rational geometry is a sum of polynomials. Rational geometry is a ratio of sums of polynomials. Rational geometry is considerably more complex mathematically. Therefore:
- It may not be transferable to downstream CAD packages that can’t deal with complex descriptions
- It can be slower to manipulate when modeling, and slower to render.
The following tables lists the differences between the two types of geometry.
| Nature | Pros | Cons |
|---|---|---|
| Non-rational | More flexibility for transformations.Faster. | Sacrifices some precision for modeling flexibility. |
| Rational | Precise geometry (that is, exact conics). | Weighted CVs not supported by many CAD packages. Weighted CVs harder to manipulate.Creates multi-knots.Slower to display and render. |
This illustration shows two circles drawn with the two types of geometry.
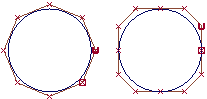
- The circle on the left is a non-rational curve with CVs that are all weighted equally. To have a non-rational curve, all weights must be 1.0.
- The circle on the right is a rational curve with different weights applied to the CVs, and multi-knots.
You can see the difference in two ways:
If you attach a radius measurement to the circles, the non-rational circle is not a perfect circle (although it is close): it has different radii depending on where you measure. The rational circle is a perfect circle.
Attach curve curvature combs to the circles. The curvature on the non-rational circle on the left varies. The curvature of the rational circle on the right is constant.