To Create an Arc/Bearing Survey Intersection

You can calculate the intersection between a line and an arc. The line is established by a point, bearing, and offset.

To calculate the intersection of an arc and bearing line in the Survey Command Window

1. In Toolspace, on the Survey tab, right-click the network to edit, and click Survey Command Window.
2. Click Intersections menu 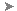Arc/Bearing.
3. Enter the point identifier of the arc center.
4. Enter the radius of the arc.
5. Enter the starting point identifier of the line.
6. Enter the bearing of the line.
7. Enter the quadrant of the line.
8. Enter an offset.
9. Enter one of the following options:
   • N: To select the northern-most intersection.
   • S: To select the southern-most intersection.
   • E: To select the eastern-most intersection.
   • W: To select the western-most intersection.
   • R: To select the solution nearest.
   • F: To select the solution farthest.
   • 1: To select intersection 1.
   • 2: To select intersection 2.
   • A: To select all the intersections.
   • P: To pick the intersection with your pointing device

To calculate the intersection of an arc and bearing line, using the survey command language

1. In Toolspace, on the Survey tab, right-click the network to edit, and click Survey Command Window.
2. At the Command line, enter:

   ARCB [point] [radius] [point 1] [bearing] [quadrant] [offset]

Command Line Example

NE 1 100 100

NE 2 200 200

ARCB 2 200 1 50 1 -50

! INTERSECTION # 1 NORTH:372.285978 EAST:301.575300

! INTERSECTION # 2 NORTH:98.424700 EAST:27.714022

Intersections are located between an arc radius of 200 with its center at point 2 and a bearing of 50.0000 drawn from point 1 with an offset distance of 50 to the left.

Command Syntax

ARCB [point] [radius] [point 1] [bearing] [quadrant] [offset]

Parameter	Definition
point	The radial point. This is an existing point that is used as the center point for the arc.
radius	The radial distance. This is the distance in feet or meters from the radial point to the arc.
point 1	The existing point from which a vector extends. It can be any type of point including a figure point.
bearing	The bearing of the line from the existing point. A bearing establishes a direction for the vector and is expressed in current angle units.
quadrant	The quadrant in which the bearing exists. The possible values are: 1 (NE), 2 (SE), 3 (SW), and 4 (NW).
offset	The offset left or right from the vector. This acts as if the line is moved X feet. An offset to the right is a positive number, and an offset to the left is a negative number. If you do not want an offset, then use zero for the offset.