Puck Criterion
The Puck criterion identifies fiber failure and inter-fiber failure in a unidirectional composite.
The Puck criterion also separates fiber failure into two different physical modes. To use the Puck failure criterion, you must specify two pieces of information.
- Composite Material Type: Either a carbon fiber reinforced polymer (CFRP) or a glass fiber reinforced polymer (GFRP) must be specified.
- Selected Fiber Properties: Longitudinal modulus, Longitudinal Poisson ratio.
Fiber Failure
The Puck criterion recognizes two different modes of fiber failure, the first being a tensile failure, and the second being a compressive "fiber kinking" failure. The tensile fiber failure criterion is

and the compressive "fiber kinking" failure is
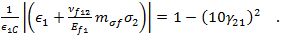
In the above fiber failure criteria:
In the above equations, the tensile equation is evaluated if 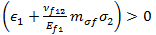 , and the compressive criterion is evaluated if
, and the compressive criterion is evaluated if 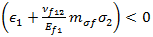 .
.
Inter-Fiber Failure (Matrix Cracking)
In the Puck criterion, inter-fiber failure encompasses any matrix cracking or fiber/matrix debonding. The Puck criterion recognizes three different inter-fiber failure modes, referred to as modes A, B, and C. These inter-fiber failure modes are distinguished by the orientation of the fracture planes relative to the reinforcing fibers.
Inter-Fiber Failure Mode A:
Mode A corresponds to a fracture angle of 0°. The criterion is invoked if the transverse stress in the composite is greater than 0 (thus indicating a transverse crack perpendicular to the transverse loading).
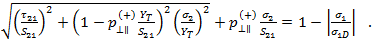
Inter-Fiber Failure Mode B:
Mode B corresponds to a transverse compressive stress (inhibiting crack formation) with a longitudinal shear stress which is below a fracture resistance (coupled with empirical constants).

The above criterion is evaluated if
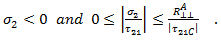
Inter-Fiber Failure Mode C:
Mode C corresponds to a transverse compressive stress (inhibiting crack formation) with a longitudinal shear stress which is significantly large enough to cause fracture on an inclined plane to fiber axis. The failure criterion for Mode C is
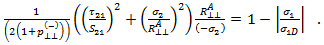
The above criterion is evaluated if
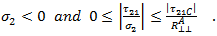
Description of Coefficients and Terms Used in the Inter-Fiber Failure Criteria
In the discussion that follows:
To establish a connection between 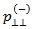 and
and 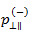 , it is assumed the following relationship holds
, it is assumed the following relationship holds
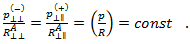
Therefore, 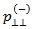 is given by
is given by
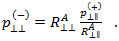
where 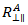 is assumed to be the same as S21, which allows
is assumed to be the same as S21, which allows  to be expressed as
to be expressed as
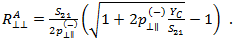
Puck and Mannigal (2007) provide the following recommended values for 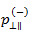 and
and 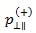 .
.

Puck also defines 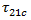 as
as
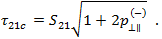
Finally, we must define  . This is a "degraded" stress in the composite allowing for pre-fiber failure breakage of individual fibers, which causes localized damage in these areas in the form of microcracking and debonding. To account for this weakening effect, Puck degrades the fracture resistances (R) by a weakening factor
. This is a "degraded" stress in the composite allowing for pre-fiber failure breakage of individual fibers, which causes localized damage in these areas in the form of microcracking and debonding. To account for this weakening effect, Puck degrades the fracture resistances (R) by a weakening factor 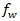 . Puck defines two equations for this. The first is for the generalized weakening factor.
. Puck defines two equations for this. The first is for the generalized weakening factor.
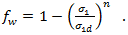
The second is to give another expression of the weakening factor to keep the fracture conditions homogeneous and of first degree with respect to the stresses.
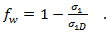
The Helius PFA implementation of the Puck criterion utilizes only the in-plane stress components of the 3-D stress state. In this case, the two equations above should be equivalent expressions since there are no iterative calculations on fracture planes being performed. Therefore, we can write
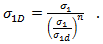
Based on the recommendations of Puck, Helius PFA uses n=6 for the exponent and empirically computes 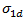 as 1.1XT or -1.1XC depending on the sign of
as 1.1XT or -1.1XC depending on the sign of 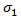 .
.
It should be emphasized that the Helius PFA implementation of the Puck criterion only uses the in-plane components of the 3-D stress and strain state, i.e., σ13, σ23, σ33, are not used to evaluate material failure.
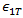
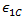
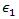
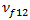
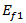
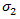
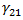
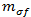
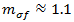 , and for glass fibers
, and for glass fibers  .
.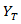
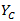
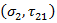 fracture envelope.
fracture envelope.