Nonlinear Elastic Fiber
When unidirectional composites are loaded to large fiber-oriented axial strains they tend to exhibit nonlinear elasticity.
The nonlinear elasticity, which primarily affects the composite E11, can be attributed to alignment of crystallites in the fiber [21]. The crystallites become more aligned in longitudinal tension, resulting in increasing stiffness. The opposite occurs in fiber compression as the crystallites become disoriented, causing a decreasing stiffness. When the fibers are loaded in tension, Helius PFA uses the first order model proposed by Murphey et. al. [21] to modify the modulus of the fiber with a modification to use a secant modulus (Eq. 28).

where 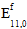 is the original fiber modulus,
is the original fiber modulus, 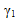 is the nonlinear parameter, and
is the nonlinear parameter, and 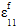 is the fiber axial strain which is assumed to be equal to the composite axial strain. Rule of mixtures is used to calculate the composite modulus based off the updated fiber modulus (Eq. 29).
is the fiber axial strain which is assumed to be equal to the composite axial strain. Rule of mixtures is used to calculate the composite modulus based off the updated fiber modulus (Eq. 29).

where φi are the volume fractions of the fiber (i=f) and matrix (i=m). All other fiber and composite elastic constants retain their original values.
Two options exist for modifying the fiber modulus in compression to model softening behavior. You can use Eq. 28 with a different nonlinear parameter (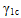 ). Alternatively, a composite modulus knock down factor, ηc, can be used to simulate the softening behavior as described in Eq. 30.
). Alternatively, a composite modulus knock down factor, ηc, can be used to simulate the softening behavior as described in Eq. 30.

where 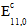 is the original composite modulus. All other fiber and composite elastic constants retain their original values.
is the original composite modulus. All other fiber and composite elastic constants retain their original values.
Eq. 31 is a limit on the value of the compressive nonlinear parameter (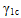 ) which prevents the modulus from going to zero before the failure has occurred.
) which prevents the modulus from going to zero before the failure has occurred.

where C1 is the absolute value of the longitudinal compressive strength.
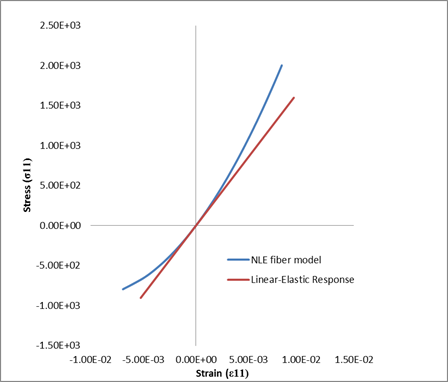
The plot below compares the composite level stress-strain behavior of a material under pure axial loading with different nonlinear parameters (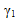 and ηc). The black dashed line represents the linear elastic response used if the nonlinear elastic fiber model is not enabled.
and ηc). The black dashed line represents the linear elastic response used if the nonlinear elastic fiber model is not enabled.
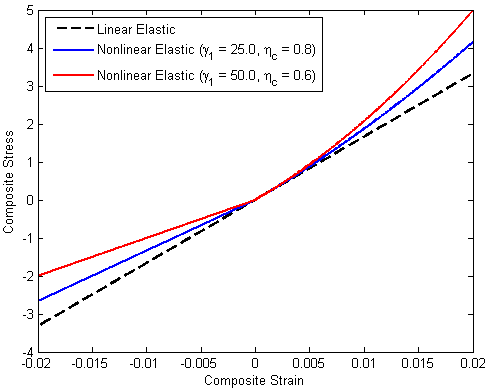
The plot below shows a comparison between the longitudinal stress-strain response using the model given in Eq. 28 for compression and tension.