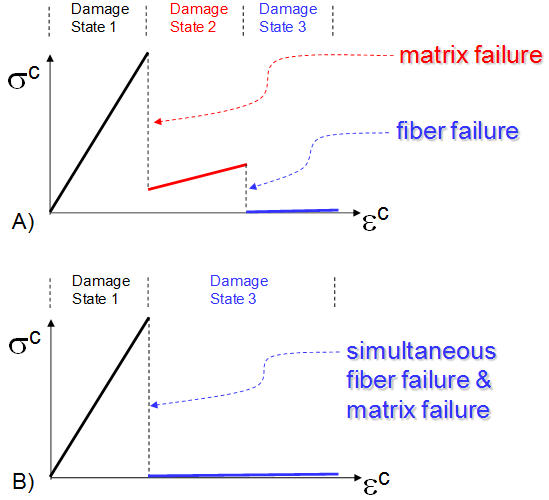
Damage States in Unidirectional Composite Materials
There are three composite damage states for unidirectional composites.
Damage State 1: Unfailed matrix constituent & unfailed fiber constituent
Damage State 2: Failed matrix constituent & unfailed fiber constituent
Damage State 3: Failed matrix constituent & failed fiber constituent
It could be argued that a fourth composite damage state is possible, namely an unfailed matrix constituent in combination with a failed fiber constituent. However, for most fiber reinforced composite materials, it is practically impossible to apply a set of loads that will cause fiber failure without also causing matrix failure. Therefore, it is assumed that regardless of the exact form of combined loading applied to a composite material, a steady increase in the magnitude of the loading will result in one of the following two possible histories for the damage state of the compositeCIR.
History 1: Damage State 1 → Damage State 2 → Damage State 3
History 2: Damage State 1 → Damage State 3
The image below illustrates the qualitative nature of these two histories. Regarding the overall responses of the composite material shown below, several issues are worthy of further discussion. First, for each of the composite material's three distinct damage states, the stiffness and thermal properties of the composite material (Cc and αc) are obtained by homogenization of the microstructure containing constituent materials that each have a status of failed or unfailed. For a failed matrix constituent in the microstructure, the matrix constituent's stiffness is isotropically reduced to a user-specified percentage (default=10%) of the original matrix stiffnessCIR. The reduced matrix stiffness directly affects the stiffness of the composite material via the homogenization process. For a failed fiber constituent in the microstructure, the fiber constituent's stiffness is isotropically reduced to a user-specified percentage (default=1%) of the original matrix stiffnessCIR. The reduced fiber stiffness directly affects the stiffness of the composite material via the homogenization process.
Second, a separate MCT decomposition must be formulated for each of the three composite damage states shown below. Recall that the MCT decomposition requires the use of linear constitutive relations where the individual components of Cc, Cf, Cm, αc, αf, and αm are simply constants. Generally speaking, these constants differ from one linear segment of the response to the next, thus the MCT decomposition is different in each section. By limiting the overall response of the composite to three distinct damage states, the process of determining the MCT decomposition constants needed for each segment of the response can be performed once. The resulting constants are stored in a database. Then, depending upon the discrete damage state of the composite, the appropriate set of MCT decomposition constants can simply be retrieved from the database. This feature contributes significantly to the overall computational efficiency of Helius PFA.
Finally, it should be emphasized that in the progressive failure analysis of large composite structures, the use of a highly discrete material response (as shown below) does not lead to a corresponding highly discrete response for the composite structure as a whole. In fact, the predicted overall progressive failure response of the composite structure is often quite smooth up to the ultimate failure load. The reason for this non-intuitive result is that the discrete material response (shown below) is being applied independently at thousands (or millions) of different Gaussian integration points distributed throughout the structure. Provided that the stress level varies from point to point in the structure, we can expect that during any particular load increment of the composite structure, only a very small percentage of these Gaussian integration points will experience a failure. Hence, the structure responds smoothly despite the use of highly discontinuous constitutive relations.