Examine how oscillating stresses are handled for progressive fatigue.

The discussion on the preceeding pages presents a method for reducing the stress tensor to a single scalar value. We now turn to the problem of how to account for oscillating stress. The nomenclature of stress ratio R and mean stress σm are typically introduced to describe simple sinusoidal loadings that vary from some minimum stress σmin to some maximum stress σmax, where

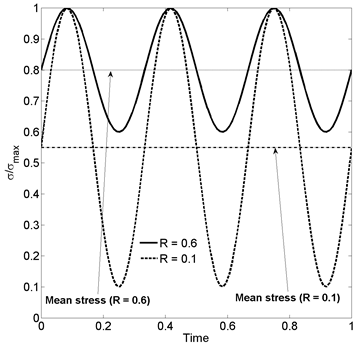
Consider the load histories shown above for R = 0.1 and R = 0.6. If stress is the only quantity varying with time, the bond breaking rate as a function of time can be written as

and the bond healing rate can be written as

By integrating Eq. 52 and 53, it can be shown that kinetic theory predicts that increasing the mean stress by increasing σmin would result in a shortening of the fatigue life with an increasing value of R. From an alternative point of view, consider the constant load case R = 1. Obviously increasing the mean stress will decrease the time to failure. But experiments on unidirectional and woven composites have shown that an increase in σmin causes an increase in the fatigue life [47, 25-26]. Thus, the oscillatory nature of the stress seems to present an additional physical feature that is not present under constant load.

The additional physical feature is temperature change in the polymer during cycling. Experimental results on pure polymers have shown that significant heating of the polymer occurs with an increase in the oscillating stress amplitude [28, 35] or an increase in the frequency [48]. For kinetic theory to properly predict fatigue life for any load history, this temperature increase must be accounted for. For a sinusoidal cycle, the rate of energy dissipated per second is given by [28]:

where f is the oscillation frequency, J'' is the loss compliance, and σa is the stress amplitude. We assume the temperature increase is proportional to the energy dissipated. The temperature T used in Eq. 40 is calculated from the nominal temperature T* such that

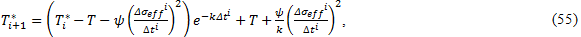
where ψ is a constant of proportionality, k is the Newton's Law of cooling constant, Δσeff is the magnitude of effective stress change over a span of time Δt, and n is the number of different stress ranges per cycle [26]. The graphic below shows how the values of Δσeff and Δt are determined during a single loading cycle.

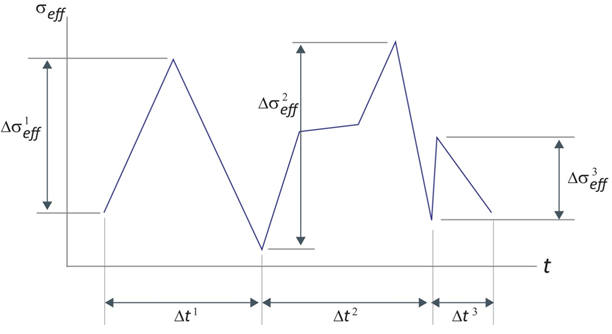
Using Newton's Law of cooling within Eq. 55 allows the temperature of the material to stabilize to that of its surroundings during a long time history instead of increasing indefinitely.