Appendix D: Additional Information for Specifying Knee Strengths for Woven Material Files
One of the primary advantages of using multicontinuum theory (MCT) for composite failure analysis is that failure criteria can be applied to individual composite constituents. When constituent failure is predicted, the composite stiffness is degraded in a manner consistent with the reduction of stiffness of only the failed constituent. Although this method is computationally efficient and is the most intuitive method for approaching composite failure, woven composites present a particular challenge: standard test data do not provide any information about failure of the matrix constituent. Tensile, compressive, and shear strengths generally reported in data sheets correspond to ultimate fiber failure.
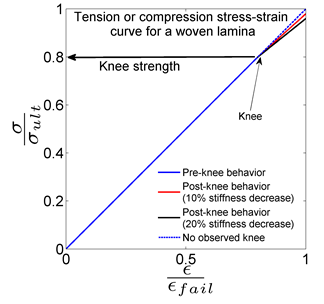
To overcome this challenge, we use what is commonly termed "knee strength" to characterize the matrix. The knee strength, which has been widely observed experimentally [1-11], is simply the stress level in a standard tensile, compressive, or shear test when the stress-strain curve changes slope. This slope change results from failure in the intra-tow matrix transverse to loading, as has been validated by acoustic emission studies (e.g., [1,7,11]). An idealization of this behavior for tensile or compressive loading is shown below, where the stresses and strains are normalized by their respective ultimate failure levels. Initially, a linear response is observed up to the knee strength. The post-knee behavior will depend on the stiffness reduction. The red and black curves correspond to a 10% and 20% stiffness reduction, respectively. The dashed curve shows the behavior if no knee were observed. Note that the knee may not be immediately obvious from a cursory glance at the curve.
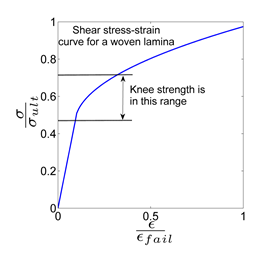
Shear behavior in woven composites is complicated by the presence of nonlinear elastic behavior. Thus, unlike the case of tensile or compressive tests, the knee strength is not sharply defined. The choice of knee strength here is a matter of engineering judgment. The curve below shows a typical shear stress-strain curve, as well as a suggested range for the choice of knee strength.
As we have shown, knee strengths can be obtained from examination of tensile, compressive, and shear stress-strain curves for a woven lamina. However, you may not have access to these curves. In the event that the knee strengths are not known, Composite Material Manager can automatically calculate reasonable knee strengths on the fly so that matrix failure in the woven composite can still be captured. The automatic calculation currently utilized begins by assuming that the shear knee strength is 75% of the ultimate shear strength. The tensile and compressive knee strengths are taken to be 75% of the respective ultimate strengths for glass/epoxy weaves and 85% of the respective strengths for carbon/epoxy weaves. Following this initialization, the tensile knee strength is adjusted to ensure that transverse tensile stresses in the matrix cause tensile failure instead of shear failure. If the knee strengths are not known, it is strongly recommended that you use the Composite Material Manager automatic calculation.
If pre-failure nonlinearity is activated, Autodesk recommends that the in-plane shear knee strength (S12k) is set to the same value as the corresponding ultimate strength (S12). The pre-failure nonlinearity calculations use the ultimate strength to calibrate the piecewise representation of the nonlinear longitudinal shear response. When the knee strength is well below the ultimate strength, the piecewise representation does not follow the experimental nonlinear shear data as well.
References
- Gao F, Boniface L, Ogin SL, Smith PA, Greaves RP. Composites science and technology 1999; 59:123-136.
- Tennyson R, Wharram G. Evaluation of Failure Criterion for Graphite/Epoxy Fabric Laminates. Toronto, Ontario: University of Toronto, 1985.
- Naik N, Ganesh V. Journal of composites technology and research 1994; 16:3.
- Fujii T, Amijima S, Lin F. Journal of composite materials 1992; 26:2493-2510.
- Gentz M, Armentrout D, Rupnowski P, Kumosa L, Sutter J, Kumosa M. Journal of composites technology and research 2003; 25:22-34.
- Lomov SV, Bogdanovich AE, Ivanov DS, Mungalov D, Karahan M, Verpoest I. Composites part a: applied science and manufacturing 2009;40:1134-1143.
- Takeda T, Takano S, Shindo Y, Narita F. Composites science and technology 2005; 65:1691-1702.
- Tang X, Whitcomb JD. Journal of composite materials 2003; 37:1239-1259.
- Dasgupta A, Agarwal R, Bhandarkar S. Composites science and technology 1996; 56:209-223.
- Roy AK. Composites science and technology 1998; 58:1793-1801.
- Ivanov DS, Lomov SV, Bogdanovich AE, Karahan M, Verpoest I. Composites part a: applied science and manufacturing 2009; 40:1144-1157.