Appendix F: Additional Information and Recommendations for Fatigue Optimization

Review recommendations for optimizing materials for fatigue analyses.

Before reading this section, you are directed to the definition of an S-N data point in the Unidirectional Fatigue Tab and Save a Unidirectional mdata File sections. Consult the Theory Manual for a description of fatigue material constants and their significance to an analysis.

The material S-N data is used to optimize the correct fatigue material constants used by Composite Material Manager. The optimization process involves iterating on the fatigue constants until the calculated error between the predicted fatigue life and the known fatigue life is minimized for both the longitudinal and transverse directions. The error is calculated as

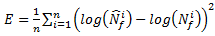
where n is the total number of data points, 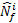is the known cycle to failure for data point i, and 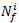is the calculated cycle to failure for data point i.

The method of steepest descent is used to increment the fatigue constants in the direction that minimizes the error described in the equation above. When a local minima is found, the optimized fatigue constants are set and used for the fatigue life prediction of the composite material. If a local minima is found instead of a global minima (which is typical), the optimized fatigue constants may yield an error greater than 1%. Errors larger than 1% are typical for most fatigue data. To ensure the material constants are acceptable, a one element model can be run to reproduce one or more S-N data point(s). Therefore, you should always check to ensure the fatigue constants and their associated converged error are physically sound.

General Fatigue Requirements

1. Experimental fatigue data contains a great deal of scatter, and the optimization scheme which determines the best material constants for a fatigue analysis gives equal weight to every data point. You should consider removing outliers from the data used to optimize fatigue properties. This will prevent unlikely S-N data points contributing to the calculation of optimized properties.

   

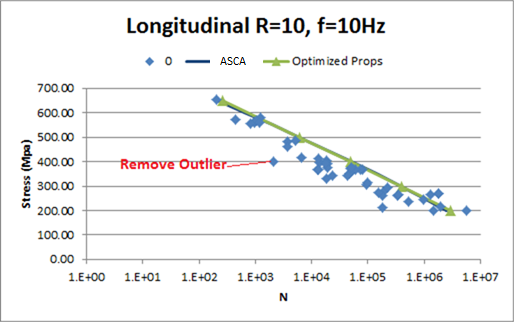
2. The greater the range of cycles to failure provided in the data will provide better optimized properties.

Unidirectional Optimization Recommendations

1. The unidirectional fatigue optimization process only requires four S-N data points, two on-axis and two off-axis data points. However, better off-axis fatigue constants will be calculated if S-N data is provided over a wide range of loading angles.
2. Providing data at different load ratios (R) and frequencies (f) will only marginally improve the calculated fatigue constants for the current implementation, but is recommended when computing fatigue life outside at different load ratios or frequencies than the input experimental data.

Weave Optimization Recommendations

1. The woven fatigue optimization process only requires two S-N data points; currently, it is only necessary to provide experimental fatigue data with loading in the fill tow direction.
2. Providing data at different load ratios (R) and frequencies (f) will improve the calculated fatigue constants for the current implementation, and is recommended when computing fatigue life outside at different load ratios or frequencies than the input experimental data.