Appendix A.7 - Damage Evolution Method (DEVO)
(Energy-based degradation is not compatible with woven materials)
If the value of the DEVO field is INSTANT, instantaneous degradation will be used. If the value is EBD, Energy-Based Degradation will be used.
Instantaneous Degradation
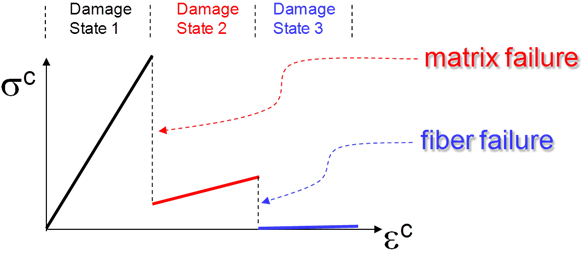
Instantaneous degradation is the default damage evolution method used by Helius PFA. When damage is predicted by the failure criterion and instantaneous degradation is used, the stiffness of the fiber and/or matrix is reduced to the minimum value instantly, as opposed to gradually. The magnitude of the reduction is controlled by the matrix and fiber degradation ratios (MPSTIF and FPSTIF). It should be noted that certain failure criterions, such as Max Stress, do not distinguish between the matrix and fiber. For these criterions, the stiffness of the composite is reduced instantly when failure is predicted, as opposed to independently reducing the matrix and fiber stiffnesses. To illustrate the effect of instant stiffness reduction, consider the graphic below which shows the stiffness of the composite at different damage states. The stiffness of the composite remains constant until matrix failure occurs, at which point the stiffness of the matrix is reduced to some ratio (MPSTIF) of the original stiffness. The reduction in matrix stiffness corresponds to a reduced composite stiffness and this reduction is applied in a single increment. When fiber failure occurs, the fiber stiffness is reduced according to FPSTIF and the composite stiffness is again reduced accordingly.
Energy-Based Degradation
The energy-based degradation feature accounts for the residual load carrying capability of a failed composite lamina embedded in a composite laminate. If the energy-based degradation feature is activated, Helius PFA will gradually reduce the stiffness of the composite after a failure criteria is triggered, instead of instantaneously reducing the composite stiffness. In this case, the failure criterion simply identifies the initiation of failure. After the failure criterion is triggered, the composite constituent stiffness is gradually reduced via a series of discrete stiffness reductions. These reductions are applied as the strain state continues to increase beyond the level present at failure initiation. When using this feature, the PFA Damage State variable can be used to identify the progression of composite damage as the strain continues to increase. For a detailed description of the energy-based nonlinearity feature, refer to the Theory Manual. The specific stiffness reductions that occur depend entirely on the failure state of the composite.
Matrix Failures:
In the case of a matrix failure, composite 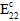 ,
, 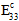 ,
, 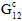 ,
, 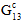 , and
, and 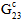 degrade linearly using the relation
degrade linearly using the relation

where  is the degraded composite property,
is the degraded composite property, 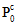 is the virgin composite property, and dm is the degradation constant due to matrix failure given by
is the virgin composite property, and dm is the degradation constant due to matrix failure given by

In the above equation, 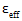 is a composite effective strain measure given by
is a composite effective strain measure given by

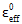 is the value of the composite effective strain at matrix failure, and
is the value of the composite effective strain at matrix failure, and 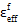 is the final effective strain value given by
is the final effective strain value given by

where Gm is the total energy dissipated in the composite before and after a matrix failure (MDE). 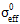 is the effective stress of the composite at matrix failure computed in the same manner as Eq. A7.1. Le is the representative element length defined by Autodesk Inventor Nastran.
is the effective stress of the composite at matrix failure computed in the same manner as Eq. A7.1. Le is the representative element length defined by Autodesk Inventor Nastran.
The definition of the final effective strain given in Eq. A7.4 assumes a linear degradation of the effective stress vs. effective strain relationship of the composite, as shown below.
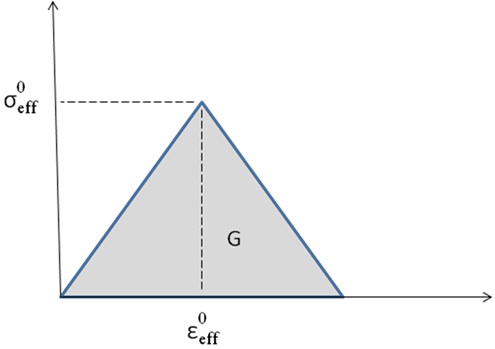
To keep the MCT decomposition intact and accurately capture stresses in the constituents after a matrix failure, properties of the matrix constituent are also degraded to enforce a consistent relationship from the micro to macro scale.
Fiber Failures:
A fiber failure event will result in a linear degradation of composite 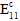 ,
, 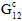 , and
, and 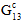 in a similar manner to the degradation of the composite properties due to a matrix failure with the effective strain being defined as
in a similar manner to the degradation of the composite properties due to a matrix failure with the effective strain being defined as

and the effective stress defined in a similar manner. However, the longitudinal shear degradation is given by

which forces the shear stiffness to be a strictly decreasing function of effective strain.
The major difference between matrix failures and fiber failures is the need for constituent information. If the fiber fails, the matrix is assumed to fail as well, and the need for constituent information is not required for further failure calculations, so constituent properties are not updated after fiber failures.
Therefore, providing the dissipation energies for matrix and fiber failure events allows the energy-based degradation scheme to compute the degraded composite and constituent properties after a failure event as a function of increasing composite strain. The energy-based degradation will alleviate some mesh dependence on a final solution and provide a robust progressive failure analysis.
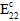 ,
, 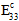 , and
, and 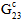 are degraded according to the Matrix Degradation Energy, otherwise
are degraded according to the Matrix Degradation Energy, otherwise 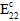 ,
, 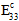 , and
, and 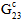 are degraded according to the Fiber Degradation Energy.
are degraded according to the Fiber Degradation Energy.A Note on Discrete Interval Partitioning:
The Energy-Based damage feature of Helius PFA uses multiple discrete intervals when linearly degrading the composite, as shown below. Each interval uses a secant modulus to define the response of the composite in that specific interval. For problems where the total energy represents something similar to an isosceles triangle, the intervals will accurately capture the response of the composite.
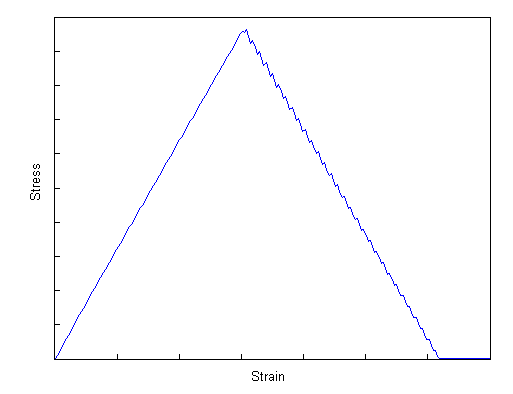
For analyses where the total energy represents a heavily skewed triangle, as shown below, interval partitioning will not accurately capture the linear softening of the composite at early strain levels. This is entirely due to the number of intervals used to achieve the most rapid and robust convergence of the problem. Specifically, the stress secant intervals at strain levels near failure retain a high stiffness and can cause a misrepresentation of the stress state of the composite. If you have analyses which must define a linear degradation curve in which the final effective strain is over 100 times the initial effective strain, please contact Autodesk for support.
