General Fluid Flow and Heat Transfer Equations

The governing equations for fluid flow and heat transfer are the Navier-Stokes or momentum equations and the First Law of Thermodynamics or energy equation. The governing pdes can be written as:

Continuity Equation:

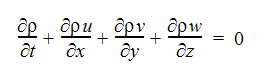
X-Momentum Equation:

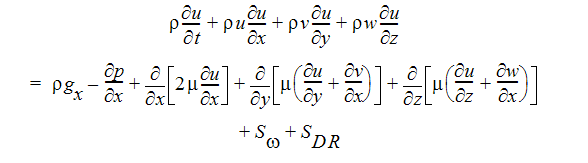
Y-Momentum Equation:

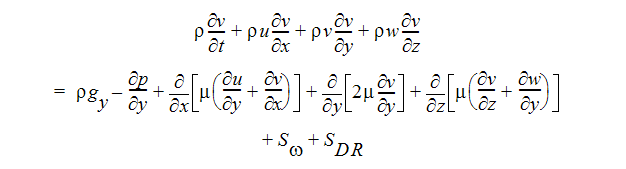
Z-Momentum Equation:

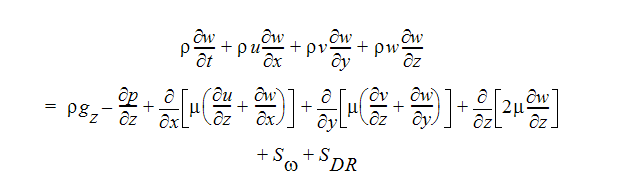
The two source terms in the momentum equations are for rotating coordinates and distributed resistances respectively. The distributed resistance term can be written in general as:

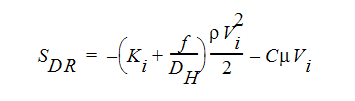
where i refers to the global coordinate direction (u, v, w momentum equation) and the other terms are described in the previous section. Note that the K-factor term can operate on a single momentum equation at a time because each direction has its own unique K-factor. The other two resistance types operate equally on each momentum equation.

The other source term is for rotating flow. This term can be written in general as:

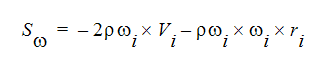
where i refers to the global coordinate direction, 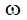is the rotational speed and r is the distance from the axis of rotation.

For incompressible and subsonic compressible flow, the energy equation is written in terms of static temperature:

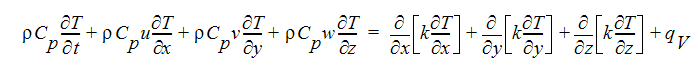
For multi-phase flows, such as steam/water, the energy equation is written in terms of enthalpy:

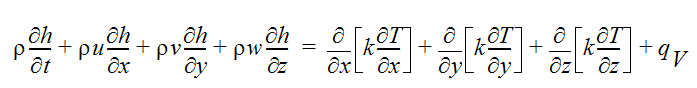
Prior to CFdesign Version 9.0, the humidity calculations were done using an enthalpy-based formulation. In this case, the enthalpy of the fluid represents the energy of both the moisture (in either its vapor or liquid state) and the air or carrier gas. However, in subsequent versions, a temperature based formulation is used for moist gas flows with a special treatment of the specific heat to account for the phase change.

For multi-phase water flows, the enthalpy is the energy of both the vapor and liquid phases.

For compressible flow, the energy equation is written in terms of total temperature:

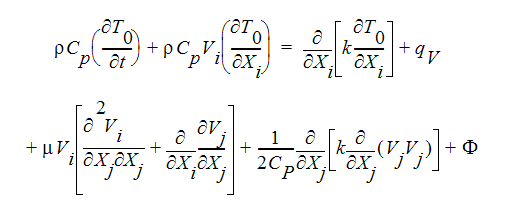
where 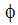is the dissipation function. Note that Einstein tensor notation is used for the total energy equation for conciseness. The last three terms are only present for compressible flows.

The variables in these equations are defined in the following Table:

Variable	Description
Cp	constant pressure specific heat
gx, gy, gz	gravitational acceleration in x, y, z directions
h	enthalpy
k	thermal conductivity
p	pressure
qV	volumetric heat source
T	temperature
t	time
u	velocity component in x-direction
v	velocity component in y-direction
w	velocity component in z-direction
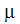	viscosity
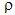	density

The continuity, momentum and energy equations represent 5 equations in the 5 unknowns: u, v, w, p, T or To. They describe the fluid flow and heat transfer under steady-state conditions for Cartesian geometries.

For axisymmetric geometries and steady-state conditions with swirl velocity component (out-of-plane component), these equations can be written as:

Continuity Equation:

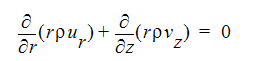
R-Momentum Equation:

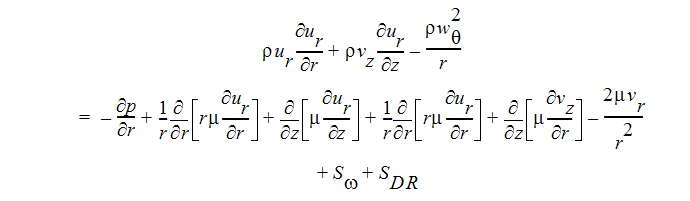
Z-Momentum Equation:

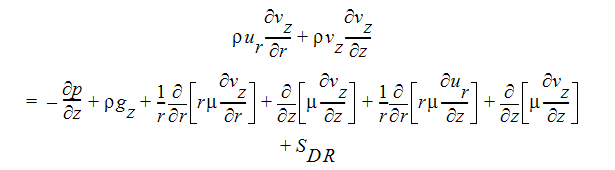
Swirl-Velocity Equation:

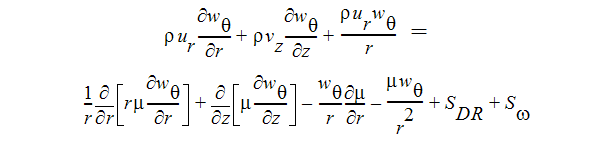
The energy equations have no additional terms for axisymmetric flows.