Matrix Solvers

The discretization process produces algebraic equations at every node. These equations form a matrix, Aij, which has as many rows as there are finite element nodes and columns enough to contain the non-zero coefficients for nodal 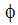values.

The classical method for solving the matrix equation is Gaussian elimination. This is a rather expensive way to get a solution because the elimination process requires at least a banded matrix for the fill produced during the decomposition. The Aij stored by Autodesk® CFD is much smaller than a banded matrix. Also, the elimination process is fairly compute-intensive. Since we are solving these equations repeatedly, this expensive elimination procedure would be prohibitively slow and arduous.

The alternative to using elimination techniques is to use iterative matrix solvers, where approximations are made to reduce the number of computations and to completely eliminate the fill process. Hence, only non-zero matrix entries are required, greatly reducing the computer storage requirements (2 - 3 orders of magnitude in 3D problems). Specifically, the approximation being made is that old values of 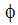can be used as estimates of current values. Repeated passes or iterations through the solver will eventually yield the same solution as the Gaussian elimination technique minus any round-off errors. However, again because of the non-linear nature of the equations, we may want to stop the iterations before we get to this point.

The simplest iterative matrix solver is the Gauss-Seidel procedure where the values are determined from:

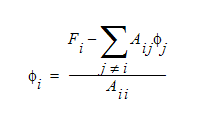
The 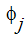values in this equation are the most recently available values. Effectively, what this does is transfer all of the off-diagonal terms to the right-hand-side of the equation. Because the number of Gauss-Seidel iterations it takes to get a decent solution is quite large, this method is not often used.

Another iterative matrix solver which gives a considerably better solution than Gauss- Seidel particularly for transport problems is the Tri-Diagonal Matrix Algorithm (TDMA). In this method, a tri-diagonal matrix equation is constructed. Here, the two columns adjacent to the diagonal of the coefficient matrix are kept and the other terms are transferred to the right-hand- side of the equations where old values of í are used. The matrix equation for TDMA can be written as:

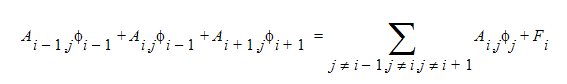
The TDMA algorithm effectively solves 1-dimensional planes of nodes simultaneously. In the transport equations, information passes from the inlet plane on to each successive plane. Hence, using the TDMA algorithm to solve the transport equations mimics this physical information flow process.

There are several iterative matrix solvers which are variants of the conjugate gradient method. Some methods are applicable only to symmetric matrices; others apply to non-symmetric matrices. All of these variants use the similar techniques to solve the matrix equation. Namely, they use a searching technique to direct the solution of the matrix equations and converge faster. They are frequently referred to as a semi-direct matrix solvers because they yield highly accurate solutions. In Autodesk® CFD, the conjugate gradient solvers will iterate through the elimination process until the convergence criterion is met or the number of iterations set by the user is exceeded.