Transient Discretization
For transient analyses, the transient terms are discretized using an implicit or backward difference method. Using the matrix algebra notation, a typical steady-state transport equation (momentum, energy, turbulence variables, scalar) can be written:
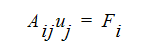
where A*ij* contains the discretized advection and diffusion terms from the governing equations, *uj* is the solution vector or values of the dependent variable (u, v, w, T, K,....) and *Fi***contains the source terms.
The transient terms in the governing equations took the form:

where 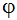 represents the dependent variable (u, v, w,....). This term is discretized using a backward difference:
represents the dependent variable (u, v, w,....). This term is discretized using a backward difference:
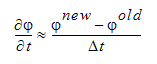
We can add this term to the matrix equation above:
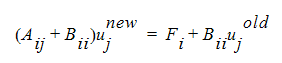
where B*ii*** is a diagonal matrix composed of terms like:
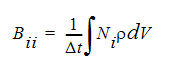
This discretized transient equations must be solved iteratively at each time step to determine all of the new variables (variable values at the latest time).