La longitud de la correa se determina en el sistema efectivo o de referencia. Por este motivo, los diámetros de referencia y efectivos se calculan primero para cada polea. La trayectoria de la correa se basa en la posición de la polea individual. La posición de la polea deslizante se ajusta para cumplir los criterios estándar de longitud de correa. El cálculo utiliza la solución de iteración para encontrar la posición adecuada de la polea deslizante que más se acerque a la posición deseada (o la actual).
Diámetros de las poleas
|
|
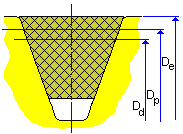
Polea acanalada |
|
D e = D w + 2 h w |
|
|
D p = D w + 2 a |
|
|
D d = D w |
|
|
|
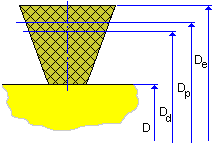
Polea plana en sentido horario |
|
D e = D + 2 h |
|
|
D p = D + 2 (h - h w + a) |
|
|
D d = D + 2(h - h w ) |
|
|
|
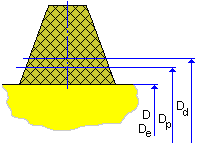
Polea plana en sentido antihorario |
|
D e = D |
|
|
D p = D + 2 (h w - a) |
|
|
D d = D + 2 h w |
Ejemplo de transmisión de potencia con 2 poleas
Este ejemplo utiliza el sistema de referencia.

Arco de contacto
![]()
Longitud de correa de referencia
![]()
Distancia al centro
![]()
Se recomienda utilizar la siguiente fórmula para calcular la distancia al centro de una nueva transmisión
0.7 (D d1 + D d2 ) ≤ C ≤ 2(D d1 + D d2 )
Significado de las variables utilizadas:
|
D W |
Diámetro nominal (de referencia o efectivo) [m] |
|
D e |
Diámetro efectivo (exterior) de polea [m] |
|
h w |
Altura nominal (para sistema efectivo h w = 0) [m] |
|
a |
Desfase de línea de paso (en el sistema efectivo es un valor negativo) [m] |
|
D |
Diámetro nominal y exterior de polea plana [m] |
|
h |
Altura de la correa [m] |
|
D d |
Diámetro de referencia de polea [m] |
|
C |
Distancia al centro [m] |
| β |
Arco de contacto [gr] |
|
L d |
Longitud de referencia de correa [m] |