Curvas de fatiga de uniones por soldadura

Se pueden utilizar distintos tipos de curvas de fatiga para determinar la resistencia a la fatiga de las uniones por soldadura. A continuación, se muestran fórmulas para curvas individuales de tensión normal y de corte.

1. Método de tensión media virtual

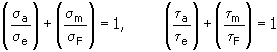
donde:

	σ a , τ a	amplitud de tensión normal (corte) [MPa, lpc]
	σ e , τ e	límite de resistencia con resistencia constante [MPa, lpc]
	σ m , τ m	tensión cíclica media [MPa, lpc]
	σ F , τ F	tensión media virtual [MPa, lpc]
	Ψ	factor de estrechamiento del diagrama de Haigh [-]
		depende del material de la junta (valores recomendados) para la tracción y el plegado Ψ<0,15...0,3>
		- para el corte Ψ <0,1...0,25>.

2. Método Godman modificado

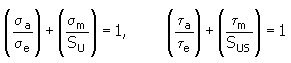
donde:

	σ a , τ a	amplitud de tensión normal (corte) [MPa, lpc]
	σ e , τ e	límite de resistencia con resistencia constante [MPa, lpc]
	σ m , τ m	tensión cíclica media [MPa, lpc]
	S U	tensión máxima de tracción [MPa, lpc]
	S US	tensión máxima de corte [MPa, lpc]
		mientras S US ≈ 0.8 S U

3. Método cuadrático (elíptico)

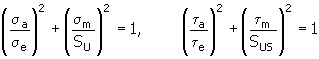
para obtener aclaraciones sobre las variables, consulte el tema 2: método Godman modificado

4. Método Gerber parabólico

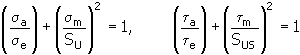
para obtener aclaraciones sobre las variables, consulte el tema 2: método Godman modificado

5. Método de Keccecioglu, Chester y Dodge

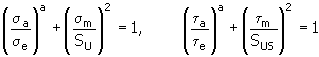
donde:

	σ a , τ a	amplitud de tensión normal (corte) [MPa, lpc]
	σ e , τ e	límite de resistencia con resistencia constante [MPa, lpc]
	σ m , τ m	tensión cíclica media [MPa, lpc]
	S U	tensión máxima de tracción [MPa, lpc]
	S US	tensión máxima de corte [MPa, lpc]
		mientras S US ≈ 0.8 S U
	a	exponente según el material de la junta [-]
		valores recomendados a <2,6...20,75>

6. Método de Bagci

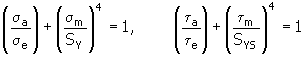
donde:

	σ a , τ a	amplitud de tensión normal (corte) [MPa, lpc]
	σ e , τ e	límite de resistencia con resistencia constante [MPa, lpc]
	σ m , τ m	tensión cíclica media [MPa, lpc]
	S Y	límite máximo de elasticidad [MPa, lpc]
	S YS	límite máximo de elasticidad [MPa, lpc]
		mientras S YS ≈ 0.577 S Y

7. Método de Soderberg

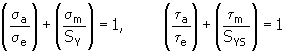
para obtener aclaraciones sobre las variables, consulte el tema 6: método de Bagci