Durante los cálculos de una losa ortotrópica, se calcula una rigidez equivalente en un nivel de sección en cada punto. Para un elemento de lámina 2D en 3D, la rigidez se determina en función de las siguientes matrices:
- Matriz de rigidez - estado de membrana D
- Matriz de rigidez para la flexión K
- Matriz de rigidez para el cortante H
Suponiendo que la ortotropía se define solo para elementos 2D y que la sección es simétrica, no es necesario determinar las matrices que combinan los estados de flexión y membrana.
Las secciones de nervios de ambos lados en una dirección, forjados reticulares en una dirección, forjados reticulares en dos direcciones y rejillas constituyen secciones simétricas, por lo que el enfoque anterior está totalmente justificado. Sin embargo, para los demás tipos, el enfoque anterior solo proporciona una aproximación.
El plano de referencia para definir la rigidez debe adoptarse en el nivel del centro de gravedad en lugar de como línea media (espesor de la pletina). Es un enfoque más correcto, especialmente si se tienen en cuenta las vibraciones transversales. No obstante, es también una aproximación cuando se calcula la rigidez, pero es mejor que adoptar el espesor como línea media.
La rigidez de la losa se determina en función de las siguientes matrices:
- Matriz de rigidez para la flexión K
- Matriz de rigidez para el cortante H
Los valores de rigidez que hacen referencia a las direcciones de la ortotropía se obtienen mediante las matrices que adoptan la forma general:
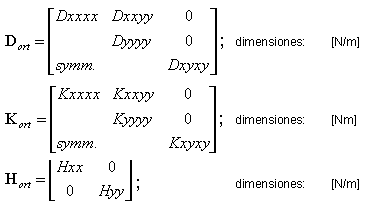
La dirección X de la ortotropía la define el usuario (definición de un vector de dirección), como cuando se define el sistema local para la presentación de resultados o armaduras V =[vx,vy,vz].
Esta es la regla utilizada para determinar cómo el vector V definido por el usuario genera la dirección del eje X del sistema de ortotropía:
"La dirección X es la dirección tangencial al plano del elemento más cercano a la dirección V definida".
Si {e 1 ;e 2 ;e 3 } constituyen una base local en el punto de elemento especificado (para pletinas en 2D, e i coincide con las direcciones de los ejes globales XG, YG), las funciones trigonométricas sin α ; cos α del ángulo a incluido entre la dirección X de la ortotropía y el eje local x1 se definen como:
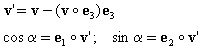
Una vez determinadas las funciones trigonométricas s = sin α ; c = cos α del ángulo a, las matrices de rigidez se transforman del sistema de ejes de ortotropía XY a las direcciones locales de un elemento, aprovechando las siguientes fórmulas:
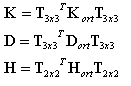
donde:
T3x3 es la matriz de transformación para el tensor de orden 2 en 2D (presentada como matriz 3x3).
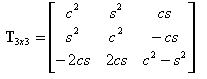
T2x2 es la matriz que presenta la transformación del vector 2D.
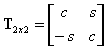
Consulte también: