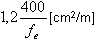Cálculos de muros de hormigón armado según NF EN 1992-1-1/NA:2007 (NF P 18-711-1)

Los muros de hormigón armado se calculan según los principios especificados en:

• NF EN 1992-1-1/NA:2007 (NF P 18-711-1)
• Recommandations professionnelles pour l'application de la norme NF EN 1992-1-1 (NF P 18-711-1) (Recomendaciones profesionales para la aplicación de la norma NF EN 1992-1-1 [NF P 18-711-1])
• EN 1992-1-1/AC:2008

MÉTODO DE CÁLCULO

El diseño del muro se basa en la hipótesis de que el muro funciona en su plano como una sección de hormigón armado. La distribución parabólica-lineal de las tensiones de compresión en la sección se adopta aquí.

Los cálculos se realizan para un muro no armado y, si es necesario, para uno con armadura. El proceso de diseño se centra en la sección inferior del muro.

El algoritmo de cálculo es el siguiente:

• Para la reducción de la carga, las cargas lineales se reducen al sistema N - M - V.
• Para calcular la capacidad de carga de un muro no armado, consulte las descripciones de los algoritmos de los cálculos de muros.
• Si la capacidad de carga de un muro no armado es menor que el impacto debido a las fuerzas reducidas verticales N, se presupone una distribución uniforme de la armadura.
• En función de las armaduras distribuidas (se adopta la mayor de las combinaciones individuales sísmicas y no sísmicas), se calcula la capacidad de carga de un muro armado (por separado para las estructuras sísmicas y no sísmicas).
• Si la tensión de compresión media en el muro o la tensión media en la abrazadera de compresión supera la tensión admisible en el hormigón, los cálculos se interrumpen. Las dimensiones de la sección del muro deben aumentarse.
• Los cálculos de compresión con flexión se realizan tomando la resistencia de la sección a partir de la resistencia del hormigón o del hormigón con armadura distribuida y teniendo en cuenta el pandeo del muro (el coeficiente a).
• La armadura para la compresión con flexión se dispone cerca de los bordes del muro (con zonas ocultas). La armadura distribuida vertical se calcula para poder soportar la fuerza N y la posible armadura resultante de la verificación del cortante y del deslizamiento. Ambos se generan a lo largo de toda la sección.

Nota: Los huecos actuales se omiten en los cálculos mediante el método clásico. La reducción de la sección no se tiene en cuenta en los cálculos de flexión con compresión ni en los cálculos de tensión de tangente. Solo se genera una armadura de construcción cerca del hueco (en el caso de los muros sísmicos es la armadura de borde mínima CV).

Algoritmo de cálculos de muros (cargas no sísmicas)

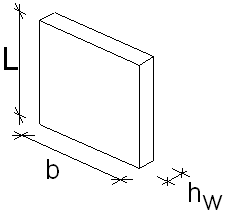
Las dimensiones básicas de los muros se muestran en el dibujo siguiente.

Se asume que:

• longitud del muro b ≥ 4 · h_w
• espesor del muro:

  a ≥ 10 cm son muros internos (y externos, pero según la norma EN todos los muros no armados deben tener ≥ 12 cm) y el usuario puede elegir en las opciones de cálculo si es un muro interno o externo.

  a ≥ 12 cm son muros externos.

• esbeltez λ ≤ 86.

A continuación, se indican los pasos individuales del algoritmo de cálculo para los muros sometidos a cargas no sísmicas:

• Cálculos de b según la ficha 12.1 (EN 1992-1-1/AC:2008)
• Cálculo de la longitud de pandeo de un muro l₀, donde l₀= β · l_w
• Cálculo de la esbeltez λ, donde λ=l₀/i
• Se comprueba la condición de la capacidad de carga del muro para el nivel inferior de este. Se comprueba la capacidad de carga de la sección del muro en cuanto a cargas verticales reducidas, y la armadura se distribuye uniformemente en toda la sección. En los siguientes pasos de los cálculos, se tiene en cuenta la capacidad de carga de un muro armado o no armado, respectivamente.
• Se comprueba la capacidad de carga de la sección de muro no reforzada para la tensión media de compresión o la tensión media en la abrazadera de compresión.

  σ _moy =N/(b · h_w) ≤ σ _ulim

  σ _band,moy =N/(b · h_w) ≤ σ _ulim

  Si la tensión de compresión media en el muro o la tensión media en la abrazadera de compresión supera la tensión admisible en el hormigón, los cálculos se interrumpen. Las dimensiones de la sección del muro deben aumentarse.

• Cálculo de la capacidad de carga del muro no armado N _ulim y de la tensión admisible σ _ulim

  Φ = min(1-2 · e_tot/h_w; 1.14(1-2 · e_tot/h_w) - 0.02 · l₀/h_w )

  Donde e_tot=e₀+e_i

  N_ulim= b · h_w · f_cd,pl · Φ

  σ _ulim = N_ulim/(b · h_w)

  Si N_umax ≥ N_ulim, la armadura para la compresión con flexión se dispondrá cerca de los bordes del muro.

• Generación de armaduras distribuidas en el muro

  La proporción mínima de la armadura vertical debe ser igual a:

  A_s,vmin = 0,002 · A_c

  La proporción máxima de la armadura vertical debe ser igual a:

  A_s,vmax = 0,04 · A_c

  La distancia entre dos barras adyacentes no debe ser superior a 3 - h_w y 400 mm

  La armadura horizontal cumple las condiciones:

  (la armadura se distribuye uniformemente sobre la altura del muro)

  A_s,hmin = max (25%A_v; 0,001 · A_c)

  La distancia entre dos barras adyacentes no debe ser superior a 400 mm

• Cálculos y generación de armaduras de bordes

  Como se indica en los supuestos del método, los cálculos de esta armadura se centran en asegurar que la flexión con compresión pueda ser soportada por una estructura; se genera en una "zona oculta" de la anchura igual a d'.

• Cálculos de la resistencia al cortante de un muro no armado

  σ _cp = N/(h_w · b)

  t cp = k · V/(h_w · b)

  σ _c,lim = f_cd - 2 · (f_ctd · (f_ctd+f_cd)) ^½

  Si σ _cp ≤ σ _c,lim:

  f_cvd= (f_ctd,pl ² + σ _cp · f_ctd,pl ² ) ^½

  Si σ _cp > σ _c,lim:

  f_cvd= (f_ctd,pl ²+ σ _cp·f_ctd,pl² - 0,25 · ( σ _cp - σ _c,lim )²) ^½

• Comprobación del cortante para muro no armado

  Si τ _cp <= f_cvd, la armadura de cortante calculada en base a los siguientes criterios debe distribuirse uniformemente a lo largo del muro:

  v_min = 0.35/ γ _c · f_ck ^½

  k = min(1+(200/b) ^½ ); 2)

  C_Rd,c =0.18/ γ _c

  σ _cp =min(0,2 · f_cd; N/(h_w · b))

  V_Rd,c = max((C_Rd,c · k · (100 · ρl · f_ck) ^(1/3)+k₁ · σ_cp )*h_w*d; (v_min+ k₁ · σ_cp ) · h_w · d) ^(1/3))

• Comprobación del cortante para muro armado

  Las cargas ELU verticales deben cumplir los siguientes criterios:

  V<=V_Rd,c

• Generación de armaduras someras y de construcción.

  Armaduras someras:

  = vertical

  

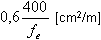
  = horizontal