Acerca de la conversión de las cargas en masas

Observaciones introductorias:

Las cargas, en su gran mayoría, se originan en la gravedad (masas). Por lo tanto, el cálculo dinámico debe tener en cuenta estas masas. Con el fin de ofrecer al usuario una conversión sencilla de las cargas estáticas (cargas de gravedad) a masas, se ha aplicado el comando especial "MASses ACTive" en el analizador de archivos de texto.

Este permite a los usuarios definir la carga una sola vez para el análisis estático y, a continuación, utilizarla para crear una distribución de masa sobre el modelo de cálculo de la estructura con el fin de realizar un análisis dinámico.

El comando necesita dos elementos para realizar una conversión correcta. El primero es el conjunto de direcciones en las que las masas están activas. Normalmente se utilizan todas las direcciones globales (X, Y, Z), ya que solo en ciertos cálculos específicos la inercia no actúa sobre todas ellas. La segunda es la magnitud de la inercia. Esta viene definida por el número de caso de la carga estática y la dirección de las cargas, que se tienen en cuenta durante la conversión. Además, se puede proporcionar un coeficiente adicional para multiplicar el valor de carga.

El carácter de la carga se transforma automáticamente en las masas: las fuerzas concentradas se transforman en masas concentradas; los momentos, en inercia rotacional; y las fuerzas distribuidas, en masas continuas.

Sintaxis:

ANA [ DIN | MOD | TRA | ARM | SISmico | ESPectral ], (afecta a todos los tipos de análisis dinámicos).

CASo (#<número> <nombre>)

MASess ACTive [X/Y/Z]

[X|Y|Z ] (MEnos|MAs) <lista_casos> COEficiente=<c>

Nota: La sintaxis anterior se ha introducido únicamente en el archivo de texto (se borra del archivo de datos una vez que se ha guardado correctamente en el programa).

Principios generales:

Consideremos r = r(x) una función de la distribución de densidad de masa dentro de un elemento determinado, mientras que N(x) será la matriz de funciones de interpolación de nudos (matriz de funciones de forma). Como base para el posterior tratamiento, se creará una matriz coherente de masas de un elemento de acuerdo con la siguiente fórmula general (1):

, (1)

donde:

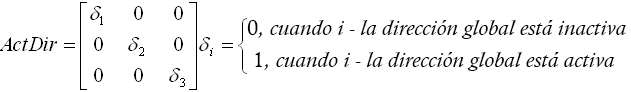
Los indicadores de actividad de dirección global se establecen mediante MASess ACTive [X/Y/Z]; es decir, cualquier dirección está activa si se especifica. Esto es consecuencia del estilo general de tratamiento de masas de Robot, por el que algunos componentes de las fuerzas de inercia pueden omitirse durante el análisis.

La matriz de masas se creará a partir de todas las cargas que pertenezcan a todos los casos de carga especificados en <lista_casos> y actuará en el elemento o nudo actual de acuerdo con las siguientes reglas:

• Cada registro de carga del caso especificado se convierte en la masa por separado y con independencia de otras cargas y masas.
• Solo pueden aparecer casos de carga simples (sin combinaciones) en la lista (sin embargo, en un caso dinámico, se puede proporcionar la lista de casos estáticos para convertirlos en masas).
• La matriz de masa total se crea como una suma de matrices de masas de todos los componentes de carga ubicados encima y de una masa predefinida debido al peso muerto de la estructura o a las masas de elementos especificadas. Por lo tanto, también se envía una parte de la matriz de masas originada a partir de las cargas a la diagonalización u omisión de la parte de inercia rotacional si se especifica mediante el parámetro COH|CON, ROT.
• El valor de la función de densidad en el punto dado se crea como el valor de la proyección del vector de fuerza actual f en el vector n de dirección global especificada única y obligatoriamente

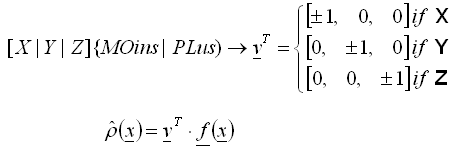  , (2)

• En cada punto de integración, solo se tienen en cuenta los valores positivos, por lo que

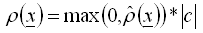  , (3)

  Nota: Las reglas anteriores están diseñadas para permitir una selección sencilla de cargas originadas por la gravedad. Como no existe una dirección de gravedad por defecto, el usuario debe realizar la especificación de la dirección mediante signos.
• Todas las direcciones utilizadas para definir la conversión de carga a masa deben ser compatibles con el tipo de estructura general actual, por lo que PLetina solo acepta la dirección Z, mientras que en otros tipos de plano solo se aceptan X e Y. Las especificaciones de dirección incompatibles se ignoran o generan una notificación de error. Los tipos estructurales 3D aceptan todas las direcciones globales.

Ejemplo:

Tomemos como ejemplo una viga con una carga central de gravedad de Fy= - 120 kN. Supongamos que el caso estático que se muestra a continuación tiene el número 3. Para calcular los modos de vibración libre de esta estructura en el caso número 10, teniendo en cuenta esta masa (Fx=Fy= 12 232 kg), se puede utilizar el siguiente comando:

ANA MOD=3 MAS=CON

CAS #10 modal

MASses ACTive X Y

Y MEnos 3

Detalles de conversión para diferentes tipos de carga

Cargas que actúan sobre elementos de viga

• carga de elemento uniforme

  [Px=<px.>/Py=<py>/Pz=<pz>] (LOCal/GLObal) (PRoyectada) ([R=<r>])([R=<r>])

  El vector de densidad de carga se transforma en direcciones globales según se especifica al definir:

  (LOCal/GLObal) (PRoyectada) ([R=<r>]), teniendo en cuenta el indicador (PRoyectada) para el tratamiento de carga, y la distribución de masa uniforme se establece de acuerdo con (2) (3)

• peso propio

  El peso propio se convierte en masa de forma equivalente a la carga uniforme del elemento

  Nota: Esta operación debe utilizarse con precaución, ya que la masa originada por el peso propio de la estructura se incluye automáticamente en los cálculos dinámicos (si solo la densidad del material es mayor que 0)
• carga de elemento variable

  (X=<x1>)[ P=<p1>] ((JUSque)(X =<x2>)[P=<p2>] ) (R=<r>) (LOCal/GLObal) (RELativa) (PRoyectada)

  la carga se transforma en direcciones globales según lo especificado al definir:

  (LOCal/GLObal) (PRoyectada) ([R=<r>])

  a continuación, la distribución de masa uniforme se establece de acuerdo con (2)(3)

  Nota: La regla (3) implica el siguiente tratamiento de la carga de señal variable para cada registro de carga (componente) por separado (no para la carga total, que es la suma de todas las cargas que actúan sobre el elemento especificado), como se muestra en la figura 1.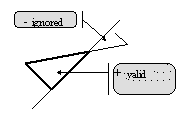

  Fig. 1

• fuerza de elemento concentrada

  [X=<x>] [F=<f>](R=<r>) (Local)(RELativa)

  La masa total m concentrada en un punto x ₀ se evalúa a partir de la representación global del vector de fuerza f de la siguiente manera:

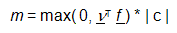  , (4)

  A continuación, se evalúa la matriz coherente de masas, como si la distribución de masas estuviera representada por la función delta de Dirac, lo que conduce a:

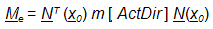  , (5)

• momento de elemento concentrado

  [X=<x>] [F=<fc>] (R=<r>) (LOCal)(RELativa)

  Dado que la especificación de la dirección de masa no afecta a las direcciones de inercia rotacional, se debe establecer una regla independiente para realizar la conversión entre el momento concentrado del elemento y la inercia rotacional de un determinado cuerpo enlazado al elemento.

  La transformación del estilo de vector de <fc> se realiza de acuerdo con los parámetros (R=<r>) (LOCal) para obtener un vector I relacionado con el sistema de coordenadas local del elemento. Para omitir la necesidad de transformar un estilo de vector incoherente (mientras se debe utilizar el tensorial), la carga debe indicarse como LOCal y no R=<r>; de lo contrario, se emitirá un aviso.

  Se supone que las coordenadas locales del elemento coinciden con el eje principal de inercia del cuerpo, por lo que 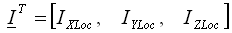representa los momentos de inercia principales en las coordenadas locales del elemento. De este modo, se genera la siguiente limitación de modelado: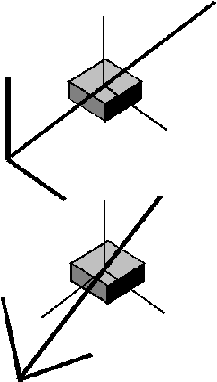

  Fig. 2

  Situación correcta                 Situación incorrecta, imposible modelar

• Momento de elemento distribuido

  [M=<m>] (LOCal)

  En esta definición, <m> es un vector que, después de la transformación del estilo vectorial al sistema de coordenadas local del elemento, representa densidades de inercia rotacional referidas al eje local del elemento según la longitud del elemento.

  Todas las nociones del momento de elemento concentrado (consulte la figura 2) se mantienen.

Cargas que actúan sobre elementos superficiales

• carga de elemento uniforme

  [Px=<px.>/Py=<py>/Pz=<pz>]

  Se evalúa el vector de densidad de carga y, a continuación, se transforma en densidad de masa según (2)(3)

• peso propio

  El peso propio se convierte en carga uniforme equivalente y se sigue tratando como se ha indicado anteriormente

  Nota: Esta operación debe utilizarse con precaución, ya que la masa originada por el peso propio de la estructura se incluye automáticamente en los cálculos dinámicos (si solo la densidad del material es mayor que 0)
• carga de elemento variable

  [P=<p1>] AU <n1>( [P=<p2>AU<n2> ([P=<p3> AU<n3>))

  En cada punto de integración, se evalúa la densidad de carga y, a continuación, se transforma en densidad de masa según (2)(3), véase la figura (1). Las reglas de integración mejorada se utilizan con:

  NGAUS = 3x3  para Q8,

   = 7  para T6,

   = 2x2 para Q4, 

   = 3  para T3.

• carga variable dentro de un contorno

  [P=<p1>] AU <n1>( [P=<p2>AU<n2> ([P=<p3> AU<n3>)) DIRección PRoyectada <v> _CONtorno <l_nudo>

  En cada punto de integración, se evalúa la densidad de carga y, a continuación, se transforma en densidad de masa según (2)(3), véase la figura (1). En el caso de que no todo el área del elemento pertenezca al contorno, la integración automática completa de la malla de puntos de hasta 100 x 100 se realiza dentro del elemento para alcanzar la precisión de integración requerida. Por lo tanto, el uso de esta opción puede ralentizar en ocasiones el proceso de evaluación de la matriz de masas.

• carga variable según la línea

  LIN

  <n1>[P=<p1>] Jusque <n2> (P=<p2>) ( [LOCal (GAMma=<gamma>)] )

  Solo la fuerza de translación se puede convertir en masa de elemento distribuida a lo largo de la línea.

  La regla de integración de tipo Gauss de 3 puntos se utiliza en cada segmento de la línea que cruza el elemento. En cada integración, el vector de densidad de carga se transforma al sistema de coordenadas global y, a continuación, se trata de acuerdo con (2)(3) para evaluar la distribución de masa a lo largo de la línea.

• carga concentrada en el punto auxiliar

  NUDo (auxiliar)

  F=<f> ( [R=<r>] )

  Solo la fuerza de translación se puede convertir en masa del elemento (en el momento de elementos de viga, se permitió la conversión de la inercia de rotación; en este caso, está prohibida). El vector de fuerza <f> se transforma, si es necesario, al sistema de coordenadas global y, a continuación, se trata según (2),(3) para evaluar el valor de masa enlazado al punto dentro del elemento; a continuación, la matriz de masas se evalúa mediante (5). El elemento al que se enlazará la masa se busca de forma automática.

Cargas sobre nudos

• fuerza concentrada

  NUDo

  F=<f> ( [R=<r>] )

  Forzar el vector <f> tratado según (2)(3) para evaluar el valor de masa nodal

• momento concentrado

  NUDo

  F=<c> ( [R=<r>] )

  Dado que la especificación de la dirección de masa no afecta a las direcciones de inercia rotacional, se debe establecer una regla independiente para realizar la conversión entre el momento concentrado del nudo y la inercia rotacional de un determinado cuerpo enlazado al nudo.

  La transformación del estilo de vector de <fc> se realiza de acuerdo el parámetro (R=<r>) para obtener un vector 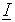relacionado con el sistema global de coordenadas. Para omitir la necesidad de transformar un estilo de vector incoherente (mientras se debe utilizar el tensorial), no debe indicarse ningún valor como LOCal o R=<r>; de lo contrario, se emitirá un aviso.

  Se supone que las coordenadas globales coinciden con el eje principal de inercia del cuerpo, por lo que 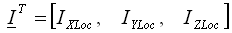representa los momentos de inercia principales en las coordenadas locales globales.

  Nota: Esta regla es diferente a las utilizadas en el caso de masa concentrada enlazada al elemento de viga.