Cálculo de la calidad de los triángulos (elementos de malla)
Cuando se genera una malla triangular, se debe definir la malla de forma que los elementos generados sean triángulos equiláteros. Otros triángulos, especialmente los triángulos obtusos, son elementos de malla "peores" desde el punto de vista del método de elementos finitos (FEM).
Suponiendo que el coeficiente de calidad de los elementos de malla triangulares esté en el rango de <0,1>, aceptamos que el coeficiente α es igual a 1 para un triángulo equilátero.
Calcule el coeficiente α de un triángulo con los vértices ABC de la siguiente fórmula:
Este algoritmo se basa en el cálculo de un producto vectorial de dos vectores en el espacio.
Cálculo de la calidad de los cuadrángulos (elementos de malla)
El cuadrángulo ideal para crear mallas cuadrangulares es el rectángulo. Se utiliza un método de cálculo de coeficientes de triángulo para calcular el coeficiente α.
Cualquier cuadrángulo ABCD se divide en cuatro triángulos solapados (ABC, ACD, ABD y BCD). El cálculo de coeficientes α se realiza para triángulos concretos: { α1, a2, α3, α4} = { α (ABC), α (ACD), α (ABD), α (BCD)}. Cuando se calculan estos coeficientes, se calcula el coeficiente de calidad del cuadrángulo.
temp1 = α1 * α3;
temp2 = α2 * α4;
if( temp1 * temp2 != 0 )
α= ( temp1 > temp2 ) ? temp2 / temp1 : temp1 / temp2;
α_rect = 0.86602540000000;
α_avg = (α_rect - fabs((α1 + α2 + α3 + α4) / 4. - α_rect))/ α_rect;
if (α_avg < α) α= α_avg;
Cálculo de un coeficiente de calidad de malla global
Existen dos métodos para calcular el coeficiente global:
- Se promedia la calidad de todos los elementos de malla (triángulos, cuadrángulos).
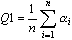
donde n: número de elemento de malla
- Se promedian los valores de calidad ponderados de todos los elementos de malla (triángulos, cuadrángulos), donde el peso es un área de elemento de malla.
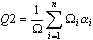
donde n: número de elemento de malla; Ω: área