El módulo de dimensionamiento de muros de hormigón armado permite definir los siguientes tipos de cargas aplicadas al muro:
- Las cargas uniformes se aplican a lo largo de la línea horizontal en un nivel arbitrario de un muro.
- Las cargas superficiales se obtienen del suelo soportado en el muro, transformadas en cargas uniformes aplicadas en cualquier nivel del muro.
- Las cargas reducidas se aplican en el plano de la base del muro en forma de fuerzas de sección reducidas que actúan en el centro de gravedad de la sección inferior del muro.
- Cargas uniformes
Las cargas uniformes y las cargas superficiales transformadas en esa forma se distribuyen en función de la distancia desde el nivel en el que se aplican. Se presupone que, en el caso de una forma arbitraria de una carga, su distribución a lo largo de la altura del muro da como resultado una carga distribuida uniformemente.
El siguiente dibujo presenta un patrón de distribución de cargas gravitatorias a lo largo de la altura del muro.
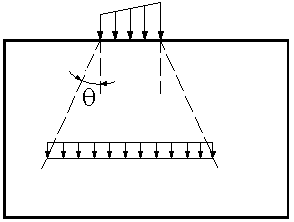
El ángulo q depende de si se trata de un muro armado. Se expresa mediante un valor de la siguiente función trigonométrica:
- tgθ = 1/3 para muros no armados
- tgθ = 2/3 para muros armados
- Distribución de cargas de los dinteles de huecos
Si hay huecos en el muro, se presupone que las cargas del dintel de hueco se transfieren por las zonas adyacentes a los bordes del hueco. La distribución de cargas depende de la posición de las cargas en relación con los bordes verticales del hueco. Se presupone que la anchura de distribución de la carga desde el dintel (anchura de las zonas en el hueco) es igual al menor de los dos valores, la mitad de la anchura del hueco y el doble del espesor del muro.
Este enfoque permite tener en cuenta las concentraciones de tensión. Por ejemplo, como en zonas adyacentes a o entre ventanas.
El módulo de muro de hormigón armado permite definir cargas que se repiten en plantas sucesivas (superiores a las del muro que se tiene en cuenta) de una estructura. Por ejemplo, si las cargas del suelo soportado en el muro son las mismas en todas las plantas superiores, puede introducir un número de plantas idénticas encima de la planta que se tiene en cuenta en el campo Número de plantas arriba del cuadro de diálogo para la definición de cargas.
En este caso de la carga en serie, se presupone que la distribución de las cargas transferidas desde plantas superiores al muro dimensionado es uniforme a lo largo de la longitud del tramo.
El método de cálculo de tensiones a partir de cargas uniformes se muestra mediante las siguientes fórmulas:
γ(x) = p(x) / a(x),
donde:
γ(x) es el valor de tensión en el punto x.
p(x) es el valor de una carga distribuida (de forma arbitraria).
a(x) es el espesor del muro.
- Cargas reducidas
Las cargas reducidas se transfieren a toda la estructura, presuponiendo que el edificio funciona como una ménsula rígida. Se presupone que las cargas reducidas se aplican en la base de una determinada planta (en el centro de gravedad de la sección de la base del muro y teniendo en cuenta los huecos). El usuario puede definir las cargas reducidas directamente en el módulo de muro.
El método de cálculo de tensiones a partir de cargas reducidas se muestra mediante las siguientes fórmulas:
- Tensiones normales en el nivel de verificación i desde la fuerza reducida N
γ(N) = N / Atot
donde:
Atot es el área total de la sección transversal de una estructura (se tienen en cuenta los huecos) en el nivel i.
- Tensiones normales en el nivel de verificación i desde el momento reducido N
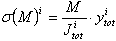
donde:
Itot es el momento de inercia de la sección inferior del muro (se tienen en cuenta los huecos) en el nivel i.
ytot es la distancia del punto que se tiene en cuenta desde el centro de gravedad de la sección de la base del muro (se tienen en cuenta los huecos) en el nivel i.
- Tensiones tangentes desde la fuerza horizontal H
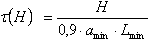
donde:
amin es el espesor del muro.
Lmin es la longitud de la estructura.
- Tensiones normales en el nivel de verificación i desde la fuerza reducida N
- Reducción de cargas uniformes
Cuando se utiliza el método clásico BAEL o se selecciona la norma ACI y también en los cálculos de cortante y deslizamiento según el método simplificado BAEL, las cargas lineales aplicadas en cualquier nivel del muro se transforman en el sistema N-M de cargas reducidas en la sección a través de la base del muro. Las cargas se reducen como se muestra en el dibujo siguiente.
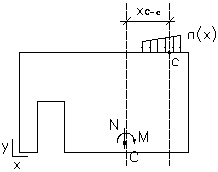
donde:
