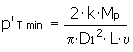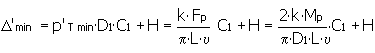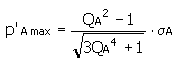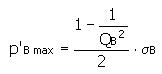Arbre creux
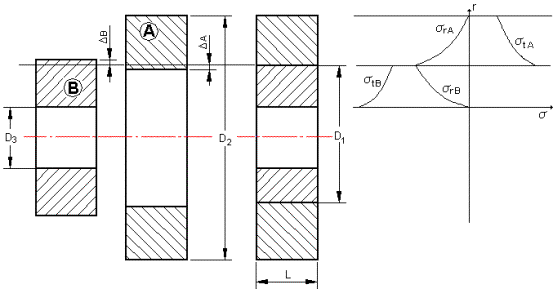
Arbre plein
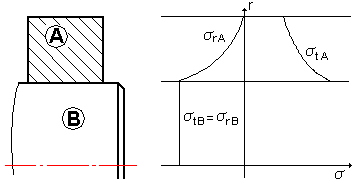
![]()
![]()
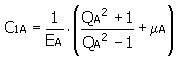
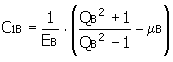
C 1 = C 1A + C 1B
Δ = p T D 1 C 1 + H
Interférence minimale possible
L'interférence minimale possible est calculée à partir de la condition de charge transmise requise. Une interférence inférieure ne peut pas transmettre la charge requise.
|
|
ou de |
|
|
|
||
Interférence maximale possible
L'interférence maximale possible est calculée à partir de la condition de résistance limite de la matière. Une interférence supérieure risque d'endommager la matière du moyeu ou de l'arbre.
|
Moyeu |
Arbre |
|
|
|
Arbre creux
Les inégalités suivantes doivent être vraies :
Δ' max ≤ p' Amax D 1 C 1 + H
Δ' max ≤ p' Bmax D 1 C 1 + H
Arbre plein
Les inégalités suivantes doivent être vraies :
Δ' max ≤ p' Amax D 1 C 1 + H
Δ' max ≤σ B D 1 C 1 + H
L'interférence minimale pour les deux inégalités est sélectionnée en tant qu'interférence maximale.
L'interférence maximale et minimale
Le calcul conçoit un ajustement d'après les normes correspondantes telles que ISO, ANSI, JIS, etc. L'ajustement standard ne peut pas dépasser les limites d'interférence maximale et minimale. L'interférence maximale et minimale destinée à une autre pièce de calcul est définie d'après l'ajustement sélectionné. Si l'ajustement correspondant ne peut pas être sélectionné, les écarts sont exprimés numériquement et calculés en divisant le champ Tolérance en deux.
Augmenter le diamètre externe de la pièce externe
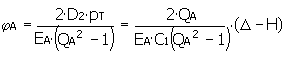
Δ' max ≤ p' Amax D 1 C 1 + H
Δ' max ≤σ B D 1 C 1 + H
L'interférence minimale pour les deux inégalités est sélectionnée en tant qu'interférence maximale.
Δ max est remplacée par Δ lors du calcul de la réduction maximale du diamètre D 2
Δ min est remplacée par Δ lors du calcul de la réduction maximale du diamètre D 2
Réduire le diamètre interne de la pièce interne
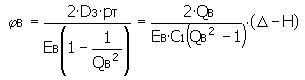
Δ max est remplacée par Δ lors du calcul de la réduction maximale du diamètre D 3
Δ min est remplacée par Δ lors du calcul de la réduction maximale du diamètre D 2
Calculer la force de contrainte
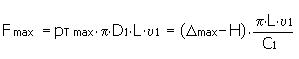
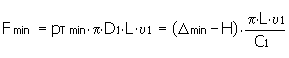
Calculer la température d'échauffement de la pièce externe
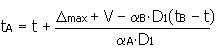
Calculer la température d'échauffement de la pièce interne
![]()
Couple
M p = Fp D 1 /2
Signification des variables utilisées :
|
M p |
Couple |
|
E A |
Module d'élasticité |
|
E B |
Module d'élasticité |
|
μA |
Coefficient de Poisson |
|
μB |
Coefficient de Poisson |
|
D 1 |
Diamètre externe de la pièce externe (moyeu) |
|
D 2 |
Diamètre de l'ajustement serré (diamètre nominal de l'ajustement calculé) |
|
D 3 |
Diamètre interne de la pièce interne (arbre) |
|
L |
Longueur de l'assemblage |
|
F pmax |
Flexion max. force de contrainte |
|
F pmin |
Longueur fonctionnelle min. force de contrainte |
|
k |
Facteur de sécurité |
| ν |
Facteur de serrage |
|
ν 1 |
Facteur de serrage pendant la pression |
|
σ A |
Dilatation thermique de la pièce externe (moyeu) |
|
σ B |
Dilatation thermique de la pièce interne (arbre) |
|
H |
Lisse de surface |
|
V |
Jeu d'assemblage |
|
P max |
Flexion max. Pression de contact |
|
P min |
Longueur fonctionnelle min. Pression de contact |
|
p' Tmin |
Pression de contact minimale possible |
|
p Tmin |
Pression de contact minimale possible |
|
p Tmax |
Pression de contact maximale |
|
p' Amax |
Pression admissible sur le perçage de la pièce externe |
|
p' Bmax |
Pression admissible sur le perçage de la pièce interne |
| Δ |
Interférence |
|
Δ' min |
Interférence possible minimale |
|
Δ' max |
Interférence possible maximale |
|
Δ min |
Interférence minimale |
|
Δ max |
Interférence maximale |
|
α A |
Coefficient de dilatation thermique de la matière de la pièce externe |
|
α B |
Coefficient de dilatation thermique de la matière de la pièce interne |
|
t |
Température de base |