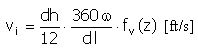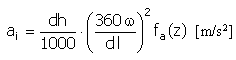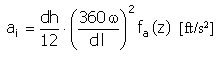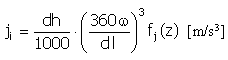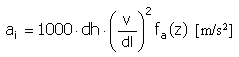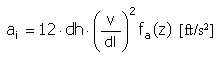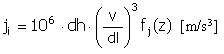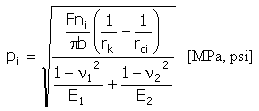Données d’entrée :
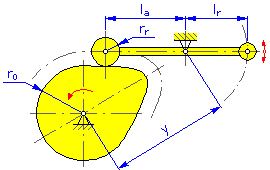
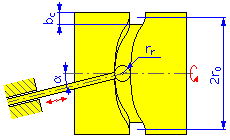
- Rayon de base r 0 (cames en disque et cylindriques)
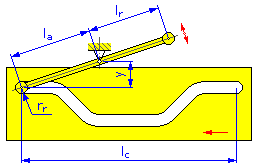
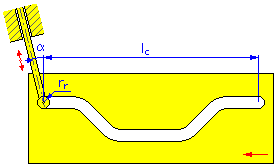
- Longueur du mouvement l c (cames linéaires)
- Largeur de came b c
- Rayon du galet r r
- Largeur du galet b r (pour le cylindre en forme de suiveur)
- Excentricité e (Cames en disque pour le suiveur de translation)
- Angle d'excentricité α (Cames linéaires et cylindriques pour le suiveur de translation)
- Distance de pivotement y (Cames en disque et linéaires pour le bras pivotant)
- Longueur du bras l a (cames en disque et linéaires pour le bras pivotant)
- Bras de réaction l r (cames en disque et linéaires pour le bras pivotant)
- Vitesse {14525 (Cames en disque et cylindriques)ω
- Vitesse v (cames linéaires)
- Force sur galet F
- Poids des éléments accélérés m
- Capacité nominale du ressort c
- pression admissible p A1
- Module d’élasticité de la matière de la came E 1
- Coefficient de Poisson de la matière de la came μ 1
- Pression admissible p A2
- Module d’élasticité de la matière du suiveur E 2
- Coefficient de Poisson de la matière du suiveur μ 2
|
Came en disque |
|
|
|
|
|
Came linéaire |
|
|
|
|
|
Came cylindrique |
|
 |
|
|
Diamètre externe = 2r 0 + b c |
|
|
Diamètre interne = 2r 0 - b c |
|
Segments de came
- Fonction du mouvement f y (z) [ul]
- Rapport inverse k r (uniquement pour les mouvements Parabolique et Parabolique avec pièce linéaire)
- Pièce linéaire k l (uniquement pour le mouvement Parabolique avec pièce linéaire)
- Position de départ du mouvement l 0 [°; mm, po]
- Position de fin du mouvement l [°; mm, po]
- Longueur du mouvement de segment dl = l - l 0 [°; mm, po]
- Levage au début h 0 [mm, po]
- Levage en fin h max [mm, po]
- Levage du segment d h = h max - h 0 [mm, po]
Dépendances de levage
Came en disque et cylindrique
Angle de rotation de la came ϕ i [°]
Position relative réelle dans le segment : z i = (ϕ i - l 0 ) / dl (plage : 0 à 1)
|
Levage |
y i = dh f y (z) [mm, po] |
|
Vitesse |
|
|
|
|
|
Accélération |
|
|
|
|
|
Impulsion |
|
|
|
Came linéaire
Position de mouvement de la came l i [mm, po]
Position relative réelle dans le segment : z i = (l i - l 0 ) / dl (plage : 0 à 1)
|
Levage |
y i = dh f y (z) [mm, po] |
|
Vitesse |
|
|
Accélération |
|
|
|
|
|
Impulsion |
|
|
|
Fonctions de mouvement
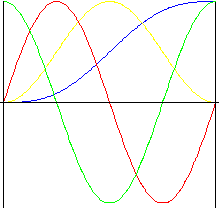
Cycloïdale (sinusoïdale étendue)
Ce mouvement présente d'excellentes caractéristiques d'accélération. Etant donné qu'il engendre de très faibles niveaux de bruit, de vibration et d'usure, ce mouvement est souvent utilisé avec des cames à grande vitesse.
|
|
Levage |
|
|
Vitesse |
|
|
Accélération |
|
|
Impulsion |
|
Levage |
f y (z) = z - 0.5/π sin(2πz) |
|
Vitesse |
f v (z) = 1 - cos (2πz) |
|
Accélération |
f a (z) = 2π sin(2πz) |
|
Impulsion |
f j (z) = 4π 2 cos(2πz) |
Harmonique (sinusoïdal)
L'avantage de cette courbe réside dans la douceur de l'accélération et de la vitesse lors de la course. Cependant, les changements instantanés d'accélération au début et à la fin du mouvement ont tendance à provoquer du bruit ou des vibrations et à accentuer le phénomène d'usure.

|
|
Levage |
|
|
Vitesse |
|
|
Accélération |
|
|
Impulsion |
|
Levage |
f y (z) = 0.5 (1 - cos πz)) |
|
Vitesse |
f v (z) = 0.5 π sin (πz) |
|
Accélération |
f a (z) = 0.5 π 2 cos(πz) |
|
Impulsion |
f j (z) = -0.5π 3 sin(πz) |
Valeur linéaire
Simple mouvement occasionnant de gros chocs au départ et à la fin. Rarement utilisé, sauf avec des appareils rudimentaires. Nous vous recommandons de modifier le départ et la fin des mouvements que vous utilisez – Parabolique avec pièce linéaire.

|
|
Levage |
|
|
Vitesse |
|
Levage |
f y (z) = z |
|
Vitesse |
f v (z) = 1 |
|
Accélération |
f a (z) = 0 |
|
Remarque : Pour z = 0 et z = 1, la valeur correcte devrait être une valeur infinie. Le calcul ne pouvant fonctionner avec une telle valeur, il utilise une valeur nulle.
|
|
|
Impulsion |
f j (z) = 0 |
|
Remarque : Pour z = 0 et z = 1, la valeur correcte devrait être une valeur infinie. Le calcul ne pouvant fonctionner avec une telle valeur, il utilise une valeur nulle.
|
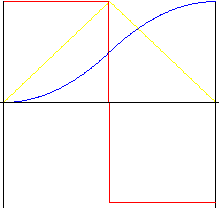
Parabolique (polynomial de 2 ème degré)
Mouvement caractérisé par une accélération la plus petite possible. Cependant, les changements soudains d'accélération au début, au milieu et à la fin du mouvement produisent des chocs. Grâce au rapport inverse, vous pouvez "rallonger" le milieu du mouvement afin de modifier les rapports d'accélération et de décélération.
symétrique (rapport inverse k r = 0.5)
|
|
Levage |
|
|
Vitesse |
|
|
Accélération |
|
pour z = 0 à 0.5 : |
|||
|
Levage |
fy(z) = 2z 2 |
||
|
Vitesse |
fv(z) = 4z |
||
|
Accélération |
fa (z) = 4 |
||
|
Impulsion |
fa(z) = 0 |
||
|
pour z = 0.5 - 1 : |
|||
|
Levage |
fy(z) = 1 - 2(1 - z) 2 |
||
|
Vitesse |
fv(z) = 4 (1 - z) |
||
|
Accélération |
fa (z) = -4 |
||
|
Impulsion |
fj(z) = 0 |
||
|
Remarque : Pour z = 0 et z = 1, la valeur correcte devrait être une valeur infinie. Le calcul ne pouvant fonctionner avec une telle valeur, il utilise une valeur nulle.
|
|||
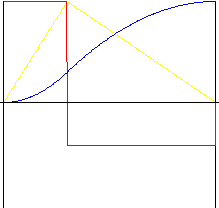
non symétrique
k r - rapport inverse (dans la plage 0.01 à 0.99)
|
|
Levage |
|
|
Vitesse |
|
|
Accélération |
|
pour z = 0 à k r : |
|||
|
Levage |
f y (z) = z 2 / k r |
||
|
Vitesse |
f v (z) = 2z / k r |
||
|
Accélération |
f a (z) = 2 / k r |
||
|
Impulsion |
f j (z) = 0 |
||
|
pour z = k r à 1 : |
|||
|
Levage |
f y (z) = 1 – (1 – z) 2 / (1 – k r ) |
||
|
Vitesse |
f v (z) = 2 (1 – z) / (1 – k r ) |
||
|
Accélération |
f a (z) = -2 / (1 - k r ) |
||
|
Impulsion |
f j (z) = 0 |
||
|
Remarque : Pour z = 0 et z = 1, la valeur correcte devrait être une valeur infinie. Le calcul ne pouvant fonctionner avec une telle valeur, il utilise une valeur nulle.
|
|||
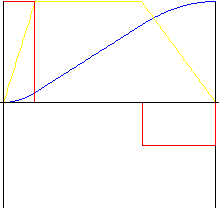
Parabolique avec pièce linéaire
Offre de meilleures accélérations et décélérations qu'un mouvement linéaire. Grâce au rapport inverse, vous pouvez "rallonger" le milieu du mouvement afin de modifier les rapports d'accélération et de décélération. Le rapport de pièce linéaire permet de définir la taille relative de la pièce du mouvement linéaire.
|
|
Vitesse |
|
|
Accélération |
|
|
Impulsion |
k r - rapport inverse (dans la plage 0.01 à 0.99)
k l - rapport de pièce linéaire (dans la plage 0 à 0.99)
k z = 1 + k l / (1 - k l )
k h = (1 - k l ) / (1 + k l )
|
pour z = 0 à k r / k z : |
|||
|
Levage |
f y (z) = k h z 2 k z 2 / k r |
||
|
Vitesse |
f v (z) = 2 k h z k z 2 / k r |
||
|
Accélération |
f a (z) = 2 k h k z 2 / k r |
||
|
Impulsion |
f j (z) = 0 |
||
|
pour z = k r / k z à r / k z + k l : |
|||
|
Levage |
f y (z) = (z - 0.5 k r / k z ) 2 / (1 + k l ) |
||
|
Vitesse |
f v (z) = 2 / (1 + k l ) |
||
|
Accélération |
f a (z) = 0 |
||
|
Impulsion |
f j (z) = 0 |
||
|
pour z = k r / k z + k l à 1 : |
|||
|
Levage |
f y (z) = 1 - k h (1 - z) 2 k z 2 / (1 - k r ) |
||
|
Vitesse |
f v (z) = 2 k h (1 - z) k z 2 / (1 - k r ) |
||
|
Accélération |
f a (z) = -2 k h k z 2 / (1 - k r ) |
||
|
Impulsion |
f j (z) = 0 |
||
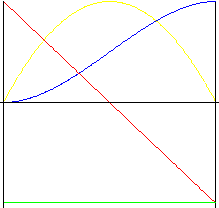
Polynomial de 3 ème degré (parabole cubique)
Mouvement occasionnant de plus petits chocs qu'un mouvement parabolique.
|
|
Levage |
|
|
Vitesse |
|
|
Accélération |
|
|
Impulsion |
|
Levage |
f y (z) = (3 -2z) z 2 |
|
Vitesse |
f v (z) = (6 - 6z) z |
|
Accélération |
f a (z) = 6 - 12z |
|
Impulsion |
f j (z) = -12 |
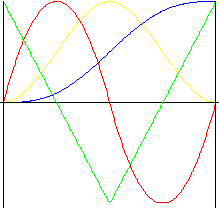
Polynomial de 4 ème degré
Mouvement occasionnant de plus petits chocs qu’un mouvement polynomial de 3 ème degré.
|
|
Levage |
|
|
Vitesse |
|
|
Accélération |
|
|
Impulsion |
|
pour z = 0 - 0.5 |
||
|
Levage |
f y (z) = (1 - z) 8z 3 |
|
|
Vitesse |
f v (z) = (24 - 32z) z 2 |
|
|
Accélération |
f a (z) = (48 - 96z) z |
|
|
Impulsion |
f j (z) = 48 - 192z |
|
|
pour z = 0.5 - 1 |
||
|
Levage |
f y (z) = 1 - 8z (1 - z) 3 |
|
|
Vitesse |
f v (z) = (32z - 8) (1 - z) 2 |
|
|
Accélération |
f a (z) = (48 - 96z) (1 - z) |
|
|
Impulsion |
f j (z) = 194z - 144 |
|
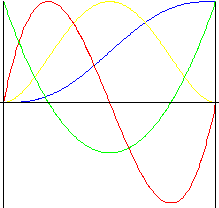
Polynomial de 5 ème degré
Mouvement occasionnant de plus petits chocs qu’un mouvement polynomial de 3 ème degré.
|
|
Levage |
|
|
Vitesse |
|
|
Accélération |
|
|
Impulsion |
|
Levage |
f y (z) = (6z 2 - 15z + 10) z 3 |
|
Vitesse |
f v (z) = (z 2 - 2z + 1) 30z 2 |
|
Accélération |
f a (z) = (2z 2 - 3z + 1) 60z |
|
Impulsion |
f j (z) = (6z 2 - 6z + 1) 60 |
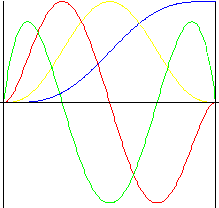
Polynomial de 7 ème degré
Douceur dans toutes les formules, y compris à l'impulsion.
|
|
Levage |
|
|
Vitesse |
|
|
Accélération |
|
|
Impulsion |
|
Levage |
f y (z) = (-20z 3 + 70z 2 - 84z + 35) z 4 |
|
Vitesse |
f v (z) = (-z 3 + 3z 2 - 3z + 1) 140z 3 |
|
Accélération |
f a (z) = (-2z 3 + 5z 2 - 4z + 1) 420z 2 |
|
Impulsion |
f j (z) = (-5z 3 + 10z 2 - 6z + 1) 840z |
Polynomial de 5 ème degré non symétrique
Similaire à un mouvement polynomial de 5ème degré, mais avec retour de levage forcé.
|
|
Levage |
|
|
Vitesse |
|
|
Accélération |
|
|
Impulsion |
|
Pièce 1 |
||
|
Levage |
f y (z) = 1 - (8 (1 - z) 3 - 15 (1 - z) 2 + 10) (1 - z) 2 / 3 |
|
|
Vitesse |
f v (z) = (2 (1 - z) 3 - 3 (1 - z) 2 + 1) (1 - z) 20 / 3 |
|
|
Accélération |
f a (z) = -(8 (1 - z) 3 - 9 (1 - z) 2 + 1) 20 / 3 |
|
|
Impulsion |
f j (z) = (4 (1 - z) 2 - 3 (1 - z)) 40 |
|
|
Pièce 2 |
||
|
Levage |
f y (z) = (8z 3 - 15z 2 + 10) z 2 / 3 |
|
|
Vitesse |
f v (z) = (2z 3 - 3z 2 + 1) z 20/3 |
|
|
Accélération |
f a (z) = (8z 3 - 9z 2 + 1) 20/3 |
|
|
Impulsion |
f j (z) = (4z 2 - 3z) 40 |
|
Harmonique double
Douceur dans toutes les formules, y compris à l'impulsion avec retour de levage forcé.
|
Pièce 1 |
||
|
Levage |
f y (z) = cos(0.5π (1 - z)) 4 |
|
|
Vitesse |
f v (z) = π (0.5 sin(πz) - 0.25 sin(2πz)) |
|
|
Accélération |
f a (z) = 0.5 π 2 (cos(πz) - cos(2πz)) |
|
|
Impulsion |
f j (z) = π 3 (-0.5 sin(πz) + sin(2πz)) |
|
|
Pièce 2 |
||
|
Levage |
f y (z) = 1 - cos(0.5π z) 4 |
|
|
Vitesse |
f v (z) = π (0.5 sin(πz) + 0.25 sin(2πz)) |
|
|
Accélération |
f a (z) = 0.5 π 2 (cos(πz) + cos(2πz)) |
|
|
Impulsion |
f j (z) = -π 3 (0.5 sin(πz) + sin(2πz)) |
|
Comparaison des valeurs relatives maximales
|
Mouvement |
Vitesse |
Accélération |
Impulsion |
|
Cycloïdale (sinusoïdale étendue) |
2 |
6.28 |
39.5 |
|
Harmonique (sinusoïdal) |
1.57 |
4.93 |
15.5 |
|
Valeur linéaire |
1 |
∞ |
∞ |
|
Parabolique (polynomial de 2 ème degré) |
2 |
4 |
∞ |
|
Polynomial de 3 ème degré |
1.5 |
6 |
12 |
|
Polynomial de 4 ème degré |
2 |
6 |
48 |
|
Polynomial de 5 ème degré |
1.88 |
5.77 |
60 |
|
Polynomial de 7 ème degré |
2.19 |
7.51 |
52.5 |
|
Polynomial de 5 ème degré non symétrique |
1.73 |
6.67 |
40 |
|
Harmonique double |
2.04 |
9.87 |
42.4 |
Autres dépendances
Force sur le rouleau
|
F i = F + m a i + c y i [N, lb] |
Force normale
|
Fn i = F i / cos (γ i ) [N, lb] |
Moment
|
T i = F i r i tan (γ i ) [Nmm, lb po] |
Pression spécifique (Hertz)
|
|
|
|
b = min (b v, b k ) |