Il s’agit de l’état limite principal du dimensionnement de la semelle, c’est pourquoi (à la différence des autres états limites) il ne peut pas être désactivé lors du dimensionnement ou de l’analyse de la semelle. L’analyse de cet état consiste à comparer la valeur maximale de la force ou de la contrainte dues aux charges externes aux valeurs admissibles. Les valeurs admissibles peuvent être définies par l’utilisateur ou calculées à partir des paramètres du sol.
Dans le cas des valeurs calculées par le logiciel, il est possible d’effectuer une analyse du sol stratifié. Les valeurs des contraintes définies par l’utilisateur sont comparées à celles directement au-dessous de la base de la semelle.
La résistance du sol définie par l’utilisateur est comparée à :
- la valeur maximale des contraintes sous la semelle ou la valeur moyenne après l’activation de l’option Répartition des contraintes plastiques dans l’onglet Options de calcul pour ACI\ BS 8004:1986\ CSA\ ENV 1997-1:1994 (EC 7), EN 1997-1:2004 (EC 7) ;
- la valeur moyenne maximale pour DTU 13.12 \ Fascicule 62 Titre V \ SNiP 2.02.01-83 ;
- la valeur moyenne et la valeur maximale divisible par 1,2 pour PN-81/B-03020.
Calculs pour les normes spécifiques
- ACI \ BS 8004:1986 \ CSA
La littérature présente quelques méthodes de base permettant le calcul de la résistance du sol. Ces méthodes réduisent les calculs aux calculs des contraintes admissibles dans le sol ou de la force admissible qui leur correspond. Chronologiquement, ces méthodes sont : Terzagi (1943), Meyerhof (1963), Hansen (1970), Versić (1973, 1 975). La méthode de Hansen est utilisée avec les directives présentées dans la littérature. La formule principale de la résistance d’après Hansen est :
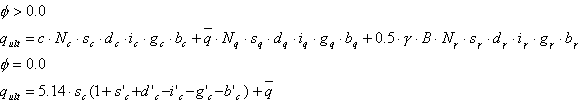
Pour les besoins du logiciel, la formule a été limitée aux cas qui peuvent être analysés dans le module de semelles isolées. On présume que les coefficients responsables de l’inclinaison de la semelle b et de l’inclinaison du talus g sont égaux à 1,0.
Puisque dans le module il n’est pas possible d’utiliser les sols dont l’angle de frottement φ = 0,0 degré, seule la première formule de Hansen est appliquée. La formule finale de calcul des contraintes admissibles pour ACI \ BS 8004:1986 \ CSA est présentée ci-dessous :
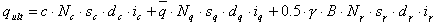
où les coefficients respectifs sont égaux à :
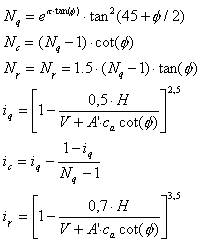
et la surface effective est A' = B' * L'
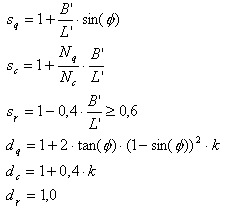
où :
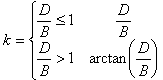
La valeur calculée qult divisée par le coefficient de sécurité SF=3,0 est comparée à la contrainte moyenne maximale dans le sol due à l’ELS
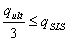
- DTU 13.12 et Fascicule 62 Titre V
Pour les normes françaises, les méthodes de calcul de la résistance du sol disponibles sont les suivantes :
Essais de laboratoire
Dans cette méthode, pour les deux normes, les calculs sont effectués d’après le point 3.21 de la norme DTU 13.12 (le fascicule ne contient pas de directives concernant la méthode d’essais de laboratoire).
La condition générale de résistance est exprimée de la manière suivante :
.
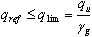qref étant une contrainte maximale moyenne présente sous la semelle en ELU, et gg étant le coefficient égal à 2 pour la combinaison ELU et à 1,5 pour la combinaison ELU comprenant les charges de vent.
Les calculs des valeurs de la résistance se font de la manière suivante :
.
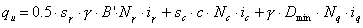Les coefficients sans unité de résistance sont égaux à :
.
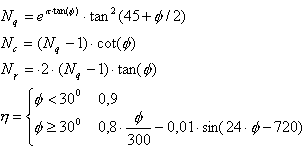Les coefficients sans unité de forme sont égaux à :
.
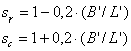Les coefficients sans unité d’inclinaison d’une charge due à la force horizontale H sont égaux à :
.
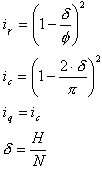Pressiométrique complète
Les calculs sont basés sur une courbe définie par l’utilisateur comme un résultat de recherche pressiométrique sur site. Le type de sol est un paramètre important sur le niveau de référence de la semelle. Il détermine les coefficients utilisés dans les calculs de la résistance et est adopté d’après l’annexe E.1. de la norme Fascicule 62 Titre V
- DTU 13.12
La condition générale de résistance peut être exprimée de manière suivante :
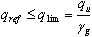(analogue à celle de la méthode d’essais de laboratoire)
Les calculs de la valeur de la résistance qu sont basés sur le point 3.22 de la norme et sont effectués de la manière suivante :
.
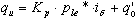Les valeurs dans la formule ci-dessus sont prises conformément à la norme, p le * étant la contrainte limite équivalente déterminée suivant la formule :
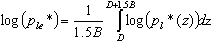
où B signifie la dimension de la semelle dans la direction étudiée.
En tant que profondeur de semelle, on prend la profondeur de semelle minimale Dmin minorée d’une profondeur d (une partie négligeable de la profondeur de semelle).
- Fascicule 62 Titre 62
La condition générale de résistance peut être exprimée de la manière suivante :
.
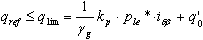Toutes les valeurs dans la formule ci-dessus sont adoptées conformément à la norme, point B.3.1,1, et les annexes B.1., E.2., F.1.
Pressiométrique de contrainte
La résistance du sol pour cette méthode est adoptée à partir de la valeur donnée directement par l’utilisateur. La valeur qu admissible (caractéristique) définie par l’utilisateur, de l’ELU ou de l’ELS, est toujours recalculée en valeur caractéristique qu, puis, à partir de cette valeur, la valeur limite de la contrainte qlim est calculée suivant les formules :
DTU 13.12
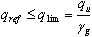
Fascicule 62 Titre 62
.
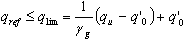De plus, si la rectification a été choisie, la rectification de la valeur donnée par l’utilisateur de la géométrie et des charges est effectuée. La valeur donnée par l’utilisateur est considérée comme la résistance qu pour la semelle ayant les dimensions unitaires (A=B=1m) et sollicitée uniquement par les charges verticales, avec la profondeur de semelle (Dmin – d). A la suite de la rectification, les dimensions réelles de la fondation, l’influence des charges horizontales et des moments (excentrements) sont prises en compte. Cela se manifeste dans les calculs des coefficients kp, idb. Le type de sol est un paramètre important sur le niveau de référence de la semelle. Les types de sols sont adoptés d’après l’annexe E.1. de la norme Fascicule 62 Titre V.
- DTU 13.12
- ENV 1997-1:1994 (EC 7)
L’analyse de la résistance du sol est basée sur le point 6.5.1, 6.5.2 et l’annexe B de la norme EC 7. La condition générale de résistance V d < R d peut être augmentée par la saisie d’un coefficient de sécurité supérieur à 1,0 (sur l’onglet Général de la boîte de dialogue Options géotechnique).
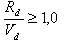
Le calcul de la valeur de résistance est effectué comme suit :
- Pour les conditions avec drainage, formule B.2 :
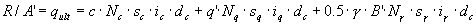
Les coefficients sans unité de charge sont égaux à :
.
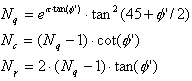Les coefficients sans unité de forme sont égaux à :
.
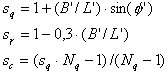Les coefficients sans unité d’inclinaison de la charge due à la force horizontale H, parallèles respectivement au bord plus long et plus court, sont égaux à :
.
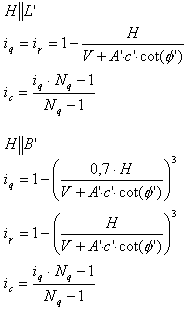Les coefficients de profondeur de la semelle sont égaux à :
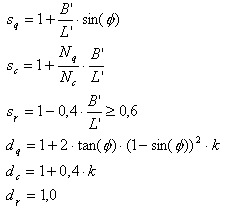
où :
.
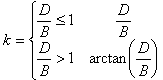- Pour les conditions sans drainage, formule B.1 :
.
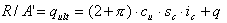Le coefficient sans unité de forme est égal à :
sc = 1,2 + 0,2 * ( B’ / L’ )
Le coefficient sans unité d’inclinaison de la charge due à la force horizontale H est égal à :
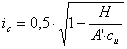
Notez que le paramètre de sol : Cohésion sans drainage - c u est appliqué ici.
- Pour les conditions avec drainage, formule B.2 :
- EN 1997-1:2004 (EC 7)
L’analyse de la résistance du sol est basée sur le point 6.5.2.1, 6.5.2.2 et l’annexe B de la norme EC 7. La condition générale de résistance V d < Rd est multipliée par le coefficient g R en fonction de la méthode de calcul. Le coefficient peut être modifié dans les Préférences de la tâche. Le calcul de la valeur de résistance est effectué de la manière suivante :
Le calcul de la valeur de résistance est effectué comme suit :
- Pour les conditions avec drainage, formule B.2 :
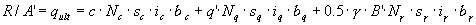
Les coefficients sans unité de charge sont égaux à :
.
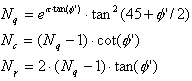Les coefficients sans unité de forme sont égaux à :
.
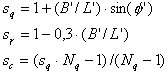Les coefficients sans unité d’inclinaison de la charge due à la force horizontale H, parallèles respectivement au bord plus long et plus court, sont égaux à :
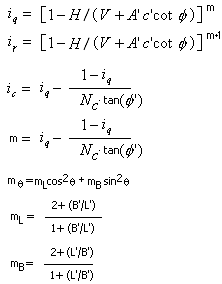
Les coefficients de profondeur de la semelle sont égaux à :
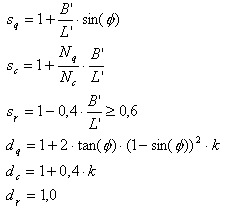
où :
.
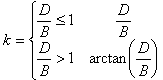- Pour les conditions sans drainage, formule B.1 :
.
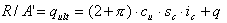Le coefficient sans unité de forme est égal à :
sc = 1,2 + 0,2 * ( B’ / L’ )
Le coefficient sans unité d’inclinaison de la charge due à la force horizontale H est égal à :
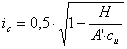
Notez que le paramètre de sol : Cohésion sans drainage - c u est appliqué ici.
Coefficients partiels pour EN 1997-1-1:2004 (EC 7)
Pour la norme EN 1997-1-1:2004, il est possible de modifier les coefficients partiels des ensembles R (pression et de résistance) et M (paramètres de sol) 2.4.7.3.4.
Les valeurs par défaut des paramètres sont disponibles dans les Préférences de la tâche.
Un ensemble (pour les actions ou leurs effets) de coefficients partiels est disponible dans la réglementation des combinaisons de la norme géotechnique (EC7_2004_geo.rgl).
- Pour les conditions avec drainage, formule B.2 :
- PN-81/B-03020
L’analyse de la résistance du sol est basée sur le point 3.3.3, annexe 1. La condition générale de résistance :
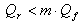
peut être augmentée par la saisie d’un coefficient de sécurité supérieur à 1,0 (sur l’onglet Général de la boîte de dialogue Options géotechnique) :
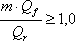
Le calcul de la valeur de résistance est effectué comme suit (Z1-2) :
.
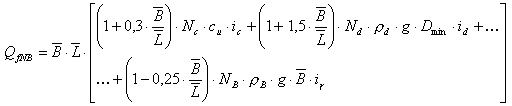Les coefficients sans unité de charge sont égaux à :
.
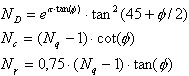Les coefficients sans unités i sont définis à partir des nomogrammes réglementaires (fig. Z1-2)
- SNiP 2.02.01-83
L’analyse de la résistance du sol est basée sur le point 2.58 -2. La condition générale de résistance (11) est :
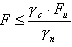
où :
γ c - coefficient environnemental
γ n – coefficient de fiabilité prenant en compte la destination de la structure
Ces deux coefficients peuvent être modifiés dans la boîte de dialogue Options géotechniques conformément à la formule présentée ci-dessous :
.
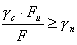En résultat du dimensionnement, on obtient le coefficient de sécurité de la structure égal à :
.
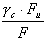Le calcul de la valeur de résistance est effectué comme suit (16) :
.
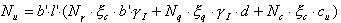Les coefficients sans unité de résistance N sont calculés conformément au tableau 7 de la norme. Entre les valeurs du tableau, une interpolation linéaire est effectuée. Les coefficients sans unité de forme X sont calculés comme suit (17) :
.
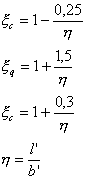