Információk a spline-görbékről

A spline-görbe olyan simított görbe, amely a görbe alakjára hatással lévő adott pontsorozaton keresztül vagy annak közelében halad.

Alapértelmezés szerint a spline-görbék 3. fokú (más néven köbös) polinomok görbeszakaszainak simításai. Ezen görbék tényleges neve nem egyenközű racionális b-spline (NURBS), de az egyszerűség kedvéért spline-görbéknek nevezzük ezeket. A harmadfokú spline-görbék a legáltalánosabbak, és azon spline-görbékre hasonlítanak, amelyeket kézzel hoztak létre rugalmas sávok használatával, az adatpontoknál lévő súlyok által kialakítva.

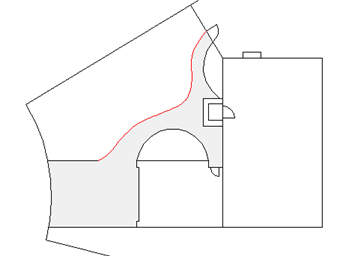
A következő példában egy spline-görbével hoztuk létre a betonsétány kiemelt határvonalát.

A vezérlő csomópontok és illesztési pontok ismertetése

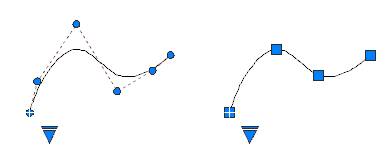
Spline-görbéket vezérlő csomópontokkal vagy illesztési pontokkal hozhat létre és szerkeszthet. A bal oldali spline-görbe a vezérlő poligonok mentén lévő vezérlő csomópontokat, a jobb oldali spline-görbe pedig az illesztési pontokat jeleníti meg.

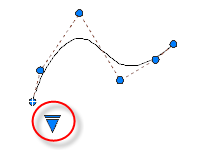
A kiválasztott spline-görbén lévő háromszög alakú fogóval válthat a vezérlő csomópontok megjelenítése és az illesztési pontok megjelenítése között. A kerek és négyzet alakú fogókkal módosíthatja a kiválasztott spline-görbéket.

Fontos: Ha a vezérlő csomópontokról az illesztési pontok megjelenítésére vált, automatikusan harmadfokúvá alakítja a kiválasztott spline-görbét. Az eredetileg magasabb fokú egyenletekkel létrehozott spline-görbék alakja ennek eredményeképpen valószínűleg megváltozik.

Spline-görbék létrehozása illesztési pontokkal

Amikor illesztési pontokkal hoz létre spline-görbéket, az eredményül kapott görbe áthalad a megadott pontokon, és a görbében lévő matematikai csomópontok térköze befolyásolja.

A csomópont paraméterezése opcióval választhatja ki ezen csomópontok térközeit, így a példában látható módon különböző görbéket hozhat létre.

Megjegyzés: Nem minden esetben ugyanaz a csomópont-parametrizálás legjobb módja. A húrhossz-parametrizálás általánosan használt módszer, és az adatkészlettől függően a négyzetgyök (centripetális) parametrizálás gyakran jobb görbéket eredményez.

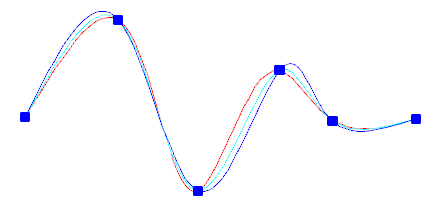
Ha a tűrés értéke 0, akkor a spline-görbe közvetlenül áthalad az illesztési pontokon. Nagyobb tűrésértékek esetén a spline-görbe az illesztési pontokhoz közel halad el. Megadhatja a spline-görbe érintő irányát mindkét végén.

Megjegyzés: Az illesztési pont módszer mindig 3. fokú spline-görbét eredményez.

Speciális esetek

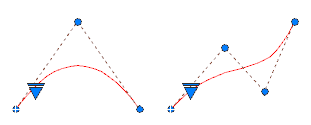
Parabola alakú spline-görbe létrehozásához adjon meg egy pontosan 3 vezérlő csomóponttal létrehozott 2. fokú spline-görbét a bal oldalon látható módon. A 4 vezérlő csomóponttal létrehozott 3. fokú spline-görbék alakja megegyezik a 3. fokú Bezier-görbék alakjával a jobb oldalon láthatóak szerint.