Castellated sections are formed by welding longitudinally-cut webs of rolled sections (rolled I-sections available in section databases). There are 2 castellated section types available: those with hexagonal or with round openings.
Castellated members can be designed only in accordance with the Polish steel code.
The following parameters specify a castellated section:
- Label - Assigns a label (name) to a section. (Robot assigns automatically a standard label with the name of the section selected from the database and the figure x denoting the new section height, such as, HP 8x36_8), where:
- x = h + c - Hexagonal openings
- x = h + c +hs - Hexagonal openings with a spacer plate
-x = H - Round openings (H is the total section height specified by the user)
- Color - Specifies a color for a section.
- Specify a section:

Hexagonal openings:
c - Cut depth
w - Distance between openings
a - Spacing of openings

Hexagonal openings with an additional spacer plate:
c - Cut depth
w - Distance between openings
hs - Height of a spacer plate
a - Spacing of openings
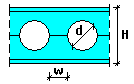
Round openings:
d - Diameter of openings
w - Distance between openings
H - Section height
- Section type - Set of options for selecting an appropriate section type.
- Gamma angle - Specifies the gamma angle of a section.
SECTIONS WITH HEXAGONAL OPENINGS
Geometrical properties
Total section height: H = h + c + h s
Cross-sectional area of the solid section
Ap = A + c * tw
Cross-sectional area of the section with an opening
Ao = A - c * tw
Cross-sectional area of the T-shaped part of a section (section with an opening)
A = 0.5 * Ao
Cross-sectional areas effective for shear
Ay = 2 * bf * tf - Cross-sectional area of flanges
Az = tw * (h - 2 * tf - c) - Cross-sectional area of the web in the weakest section - with an opening
Position of the section centroid
vz = vpz = 0.5 * H
vy = vpy = 0.5 * bf
Moments of inertia about Y and Z axes, respectively, of the section made only of flanges:
- A solid section

- A section with an opening

Arithmetic average of the moments of inertia of sections weakened and not weakened by openings
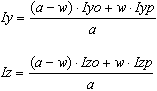
Torsional moment of inertia
SECTIONS WITH ROUND OPENINGS
Geometrical properties
d - Diameter of openings
w - Distance between openings
H - New section height (total height of the section with a spacer plate)
Cross-sectional area of a solid section
Ap = A + (H - h) * tw
Cross-sectional area of a section with an opening
Ao = A + (H - h - d) * tw
Cross-sectional area of the T-shaped part of a section (section with an opening)
A = 0.5 * Ao
Cross-sectional areas effective for shear
Ay = 2 * bf * tf - Cross-sectional area of flanges
Az = tw * (H - 2 * tf - d) - Cross-sectional area of a web in the weakest section - with an opening
Position of the section centroid
vz = vpz = 0.5 * H
vy = vpy = 0.5 * bf
Moments of inertia about Y and Z axes, respectively, of the section made only of flanges
A solid section
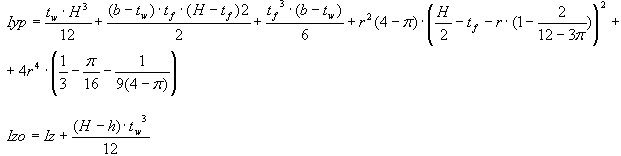
A section with an opening

Arithmetic average of the moments of inertia of the sections weakened and not weakened by openings
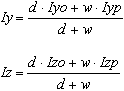
Torsional moment of inertia
Self-weight
SECTIONS WITH HEXAGONAL OPENINGS
Because a castellated section with hexagonal openings is made of a standard section (with known parameters) with almost no losses (only section ends, but they can be disregarded), its weight is the weight of the initial section. If the section includes additional spacer plates, the weight of spacer plates should be added to it:
G = g + Gs
g - Weight of the initial section
where:
h s *t w - Cross-sectional area of a spacer plate
r s - unit weight of steel
Therefore, the self-weight
SECTIONS WITH ROUND OPENINGS
The self-weight of a castellated section with round openings should be calculated as a weight of the section with a spacer plate (height 'H'), of the solid cross-section, and reduced by the weight of openings.
Weight of the initial section (from a database): g
Weight of the solid section with a spacer plate: g1 = g + rs * (H - h) * tw
Weight of the castellated section with round openings
DATABASES OF CASTELLATED SECTIONS
Castellated sections are also available in the following section databases:
- Polish section database - RPLNPro (sections with hexagonal openings made of the database sections IPE - AIPE, IN - AIN and HEB - AHEB, with hexagonal openings and a spacer plate - made of the database sections IPE - AIEP, IN - AINP and HEB - AHBP)
- Arcelor section database - ARCLRPro (sections with hexagonal openings made of the database sections I - CHXI and H - CHXH, with hexagonal openings and a spacer plate - made of the database sections IPE - CHPI and H - CHPH, with circular openings - made of the database sections I - CROI and H - CROH)
- British section database - UKSTPro (sections with hexagonal openings made of the database sections UB - CUB and UC - CUC)
- Dutch section database - TSNLPro (sections with hexagonal openings made of the database sections IPE - CIPE, HEA - CHEA and HEB - CHEB, with hexagonal openings and a spacer plate - made of the database sections IPE - CIEP, HEA - CHAP and HEB - CHBP).