Modal Analysis Parameters (Iterative Solver)

To define the modal analysis parameters for new dynamic cases in the structure, do one of the following:

Select a modal analysis case in the New Case dialog and click OK.
Select a modal analysis case in the Analysis Type dialog and click Set Parameters.

It is recommended to apply iterative solver for solving large-scale problems as it provides three methods of solving eigenvalue problems. To do so, select Iterative solver from the Structural Analysis dialog in Job Preferences.

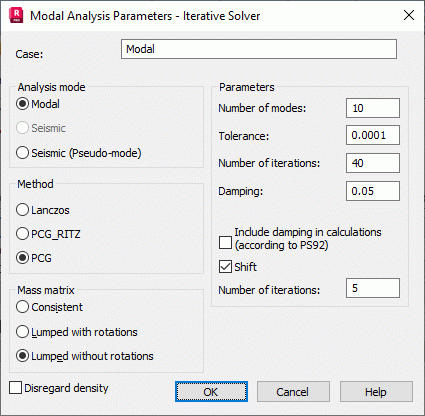
Note: You can perform a second type of modal analysis: Modal analysis recognizing static forces.

Analysis Mode

Currently the modal and seismic (pseudo) modes are available for iterative solver. Modal mode is accessible only for the preconditioned conjugate gradient (PCG) [1-4]. Seismic (pseudo) mode is accessible for modified Lanczos and Ritz-gradient (PCG_Ritz).

Method

Lanczos Method

Lanczos is a modified Lanczos method that avoids factorization of a large-scale matrix. Preconditioned conjugate gradient method (PCG) generates a collection of Lanczos vectors instead of performing back resolution of the factorized stiffness matrix. All preconditioning types defined for static analysis are available (Tools > Job Preferences > Iterative > Parameters).

Modified Lanczos is preferable in seismic and spectral analysis of large structures when many modes are required.

Required Parameters
Mass matrix type (lumped with rotations or consistent) and number of modes.

Calculation precision depends on the assumed tolerance of calculating Lanczos vectors and Number of Modes. Tolerance is assigned in Tools > Job Preferences > Iterative > Parameters and is the same as for static cases. Tolerance in the Modal Analysis Parameters - Iterative Solver dialog denotes a tolerance for a solution of a generalized eigenvalue problem including defined Lanczos vectors and cannot be smaller than 1.0e-04.

The more accounted Number of Modes, the closer low Ritz vectors will be to the appropriate eigenvalues. The sum of modal masses will be more exact.

PCG_Ritz

PCG_Ritz is a Ritz method in which the preconditioned gradient approach is used for generating a collection of basis vectors (Ritz-gradient method [5]). PCG_Ritz method is preferable for approximate quick definitions of eigenpairs during seismic and spectral analysis. It is necessary to select a multilevel method. It is also recommended to assign one aggregation level. This method will prove effective for medium-sized problems (up to 60,000 equations). All preconditioning types defined for static analysis are available (Tools > Job Preferences > Iterative > Parameters).

Required parameters
Mass matrix type (lumped with rotations or consistent) and number of modes. Precision of calculations depends on Number of Modes.

PCG

PCG is a preconditioned conjugate gradient method [1-5] that is preferable when a small number of eigenmodes is defined. For example, PCG method may prove to be very useful while applying wind loads or checking a small number of low modes obtained by means of PCG_Ritz method. All preconditioning types defined for static analysis are available (Tools > Job Preferences > Iterative > Parameters). All mass matrix types (consistent, lumped with rotations, lumped without rotations) may be applied.

Required parameters:
Number of Modes; Tolerance - precision criteria concerning stopping iterations; Number of Iterations - maximal allowable number of iterations for each mode (iteration process for each mode is stopped, if a current tolerance parameter is smaller than Tolerance or if a current iteration number exceeds Number of Iterations); Shift - takes advantage of the shift technique for convergence acceleration; Number of repetitions - determines a number of repetition (for each mode the algorithm performs iterations determined by Number of Iterations, corrects a shift value and repeats the iterations determined by Number of Iterations the number of times defined by Number of Repetitions).
Recommended parameters:
Multilevel or non-multilevel method with ICCF approach (Tools > Job Preferences > Iterative > Parameters); nModes £ 5; Tolerance = 0.01; Number of Iterations = 100 for a non-multilevel method; Shift - switched off
- Mass matrix type.
- Parameters (number of modes, tolerance, number of iterations, damping).
- Shift (with number of iterations).

Preventing Incorrect Iterative Solver Settings

A control system prevents incorrect modal analysis parameter settings for iterative solvers. It is activated once the OK is clicked to begin modal analysis. An analysis parameters prompt displays. Click Yes to accept the parameter values determined in the dialog. Click No to return to the Modal Analysis Parameters dialog and make corrections.

If an iterative solver in Seismic (Pseudo) mode is used in calculations, then do the following.

Number of aggregation levels should equal 1 (Job Preferences > Structure Analysis/ Parameters > Iterative)
The searched mode number should be entered at least three times larger than needed.
A solution convergence should be checked for the mode number presented in point 2 and a mode number twice as large. If there is a lack of convergence (clearly different eigenvalues for the mode number twice larger than for the initial number), the number of modes should be increased. Once the convergent solution is obtained the mode filtering may be applied to limit the mode number.

For such an analysis type, the Tolerance parameter in the dynamic analysis results has no practical meaning and can be ignored. If these recommendations are not followed, the error could reaching several tens of percent.

References

Gambolati G., Pini G., Sartoretto F., An improved iterative optimization technique for the leftmost eigenpairs of large symmetric matrices, J. Comp. Phys., 74: 41 - 60, 1988.
Sartoretto F., Pini G., Gambolati G., Accelerated simultaneous iterations for large finite element eigenproblems, J. Comp. Phys., 81: 53 - 69, 1989.
Papadrakakis. A partial preconditioned conjugate gradient method for large eigenproblems, Comp. Meth. Appl. Mech. Eng., 62: 195 - 207, 1987.
M.Papadrakakis, Solving large -scale problems in mechanics, John Wiley & Sons Ltd., 1993.
Fialko S., High-performance aggregation element-by-element Ritz-gradient method for structure dynamic response analysis, CAMES, 7: 537-550, 2000.