Theoretical basis of methods used during structure dynamic analysis

Introduction

This document presents the description of the dynamic analysis methods applied in Robot. The theoretical background details and examples are included in the appendices. This section is not instructional and is not aimed at detailing the Robot interface. It expounds the main ideas realized in this program.

Most of the dynamic methods in Robot are based on modal analysis results. It is necessary to understand that modal analysis methods depend on a selected type of solver. For the skyline solver, the following methods are available: block subspace iteration (BLSI), subspace iteration (SI), Lanczos and basis reduction. The methods available for the sparse direct solver include: block subspace iteration (BLSI), Lanczos and basis reduction. Whereas for the iterative solver the following methods are available: modified Lanczos (pseudo mode - see 3.5 and appendies 3A, 3B), Ritz-gradient (PCG_Ritz) and preconditioned conjugate gradient (PCG).

The sparse direct solver (SPDS) is a specific form of Gauss elimination. It is strongly recommended for analysis of medium-sized and large-scale problems (10 000 - 200 000 equations) and a good alternative for the iterative solver.

3.1. The Modal Analysis Methods

The modal analysis is comprised of two basic approaches. The eigenproblem analysis

k = 1,2,…,N (3.1)

is produced by the definition of the eigenvalues wk and eigenvectors . It is the first approach familiar to engineers. The second approach consists in the generation of basis vectors

(3.2)

and search of the Ritz approximations , (k=1,2,….,N). It is based on the method of Load dependent Ritz vectors, proposed by E.L. Wilson [1, 3] and applied into SAP2000. This approach is applied for seismic analysis and is a powerful method when there are great difficulties with obtaining sufficient mass percentage (see section 3.5).

Block subspace iteration (BLSI), subspace iteration (SI), selective orthogonalization Lanczos and basis reduction (see appendix 3A) are used when direct solvers (skyline or SPDS) are selected. Subspace iteration method is usually slow. Therefore, application of BLSI or Lanczos is strongly recommended for the analysis of medium-sized and especially large-scale problems when a large number of eigenpairs is required. Basis reduction may prove very effective for an experienced engineer; however, it requires additional information about basis nodes and appropriate basis directions.

Preconditioned Conjugate Gradient (PCG)

This method is used in the first approach, when an iterative solver is selected. Such an approach may be very efficient when small numbers of eigenmodes are extracted (at the most 5). It should be used for wind analysis rather than for seismic analysis. PCG may be used for estimation of the lowest eigenmode when a large-scale problem is met.

The second approach (which is realized by Pseudo mode Analysis) is presented in section 3.5.

Block Subspace Iteration (BLSI)

This method [1,3] is more general than Lanczos since it allows implementation of all types of mass matrices (see section 3.2) and is capable of analyzing separate structures. Iterations in a block of the constant size with immediate exclusion of converged vectors and addition of new start ones usually ensures faster computations compared to usual subspace iteration method [1-3]. Just as in Lanczos, BLSI can be applied to extract a large number of eigenpairs (till 100 - 200).

Subspace Iteration (SI)

This method can be used for analysis of all types of mass matrix [4] and for analysis of separate structures, however, in case of a large number of required modes (approximately N > 10), this method is still very time-consuming, especially for large-scale problems.

The Lanczos method [12,16,17] is a powerful method allowing one to obtain a large number of eigenpairs (N ~ 20 - 500 and more). Although it is preferable for large-scale problems, it involves the following limitations:

It is impossible to analyze separate structures
The mass matrix type should be lumped with rotations or consistent
It is impossible to disregard the material density of (in this case it suffices to assign a fictitious small density to avoid these limitations).

Basis Reduction

This method [5] is known as the improved Rayleigh-Ritz method [4] or Bubnov-Galerkin method for discrete systems. This algorithm allows one to get approximate values of the first few eigenpairs if the some information about them is known. This method requires assigning a master degree of freedom (MDOF) in order to get the reduced system. Thus, the process of creating the reduced model can be controlled. It is a powerful tool for those experienced in dynamic analysis of structures and deal with the same type of structures whose behavior is known. This method allows exclusion of undesirable degrees of freedom (DOF) from the reduced model and reduces the initial complex problem with a large number of DOF to a reduced form. This is achieved with a considerably smaller number of DOF. The experience concerning structure dynamic analysis shows that some problems can be encountered by the user when the automatic reduction methods (BLSI, SI and Lanczos are taken into account) lead to a very complex computation process. For example, the local vibration modes of single bars can lead to serious problems since the computation process seeks the eigenpairs automatically without any selection. It should be noted that for the majority of cases in real structures. Otherwise, these local vibrations will be restricted by some constraints not taken into account in the FEM model, or their contribution will be inessential to the overall system motion. Usually, the mass percentage is very small for such local vibrations. The usage of exact methods in this case will lead to the above-mentioned difficulties. However, the implementation of the approximate basis reduction method can simplify the computation process considerably.

Preconditioned Conjugate Gradient (PCG)

This method [9-13] is available for iterative solvers. Application of such a method is recommended for extracting a small number of eigenpairs when a large-scale problem is met. Implementation of the Pseudo mode (see 3.5) with modified Lanczos or PCG_Ritz is recommended if it is necessary to determine a large number of modes while running seismic or spectral analysis and an iterative solver is selected.

Ritz-gradient (PCG_Ritz)

This method [8] is available for iterative solvers in pseudo mode. It allows one to produce an approximate solution in the terms of Ritz vectors. It is a very fast method for seismic and spectral analysis of medium size (10 000 - 100 000 equations).

Modified Lanczos

This method is an extension of Lanczos method when an iterative solver is applied. It acts like the Lanczos method in pseudo mode. However, being different from Lanczos for direct solvers, it does not require factorization of a stiffness matrix. Instead, principles of the preconditioned gradient method are implemented. Such an approach is the most robust among all the dynamic methods of iterative solvers, though it often appears not to be the fastest one.

Details of all dynamic methods are presented in appendix 3A.

3.2. Mass Matrix Types

The Lumped without rotations, Lumped with rotations and Consistent mass matrices of dynamic analysis can be applied to a structure.

The Lumped without rotations and Lumped with rotations are the diagonal mass matrices. These types of mass matrices require minimum computational effort.

The Consistent mass matrix appears when a system with distributed parameters is considered. It is commonly believed that a consistent mass matrix describes inertial properties of a structure more exactly than a lumped one. However, in most cases a lumped mass matrix provides a good approximation, since it is obvious that the inertial parameters can be presented less precisely than stiffness. In fact, kinetic energy is described as displacements of a structure, but potential energy is expressed through the spatial derivative of displacements. It is a well-known fact that approximation error increases considerably during each differentiation [4]. Thus, for continual objects (solid, shells, plates), it is possible to approximate the mass parameters less precisely than stiffness for the same mesh.

Usually, Hermit polynomials are used as shape functions for bars. It is an exact solution for most of the static problems and the dynamic problems when lumped mass matrix is considered. However, exact solutions for dynamic problems of a bar with distributed masses belong to the class of Krylov functions (a specific combination of hyperbolic and trigonometric functions). It enables stiffness parameters to be presented approximately when Hermit polynomials are used simultaneously with a consistent mass matrix. It is not intended for implementing a different type of shape function for static and dynamic problems. Therefore, in most cases it is not a great benefit to complicate the dynamic model by the use of distributed mass parameters, since the approximate solution with consistent masses occurs instead of the exact solution for an approximate model (lumped masses).

Moreover, usually masses of bar structural elements (girders, columns, etc.) are negligible compared to masses of walls and roof (dead load), which are taken into account through the conversion of dead loads to masses. Such non-structural masses usually reduce the effects of distributed element masses.

For most practical cases the lumped mass matrix ensures a sufficiently precise approximation of structure inertial properties. It should be remembered that a consistent mass matrix requires considerable computational efforts if a large-scale problem is analyzed. Implementation of a consistent mass matrix must be justified before selection of such a type of matrix for analysis.

It is assumed that the mass matrix must be Consistent if the rigid links are used into computation model.

If a sparse direct solver or iterative solver is applied, element-by-element (EBE) technique is used for computation of matrix-vector product. The consistent mass matrix can never be assembled, however, all operations are performed only on the element level. For the skyline solver, a consistent mass matrix is assembled and stored in the same way as a stiffness matrix. For small problems (~3000 maximum equations) the skyline technique is faster, although it still drastically time-consuming when the size of a problem increases.

It is possible to use added masses and convert static loads to masses.

When Lanczos, PCG_Ritz or modified Lanczos (iterative solver) methods are selected, only the Lumped with rotation and Consistent mass matrices are available.

3.3. Upper Limits

It is possible to calculate all eigenvalues and eigenmodes that do not surpass a user-defined value. This value is treated as the "upper limit". When activated, Robot searches ω₁, ω₂, …, ω_n ≤ ω^*, where ω^* is the upper limit. The algorithm works in two steps. The Sturm sequence check is performed in the first step, defining the number of eigenvalues n which is smaller than the upper limit. In the next step, the algorithm generates n eigenpairs, each one smaller than the upper limit.

Lanczos and BLSI methods are recommended for the type of analysis that uses upper limits since it is necessary to obtain a large number of eigenpairs.

The criterion of mass participation percentage (see section 3.4) is ignored when upper limit is activated.

For example, problems may arise when using the French seismic code PS-92 because it is required that all frequencies smaller than 33Hz should be taken into consideration..

3.4. Mass Participation Percentage

The mass percentage for each mode (k=1,2,…,N) is defined as

where , is the mass participation factor for k eigenmode, I_dir is the vector of unit translation into the direction (dir = X,Y,Z), is the total mass into direction dir, is k-th eigenmode, .

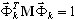The mass percentage for direction dir equals M%dir . It defines the contribution of all modes involved in motion of a structure in the considered direction.

If Modal Analysis is selected and the mass percentage for a specified maximum number of nodes is smaller than required, a prompt warns about the unsatisfactory mass percentage while calculations are continued without any corrections.

It is necessary to set the Seismic or Pseudo mode Analysis to ensure automatic search for the required mass percentage. Details are presented in section 3.5.

3.5. Analysis Modes

Modal, Seismic, and Pseudo dynamic analysis modes (regimes) are presented in this section.

Several seismic codes (UBC-97, French code PS-92) require that the sum of masses for each direction (or for horizontal directions only) should be not less than 90%. Problems may arise when achieving the required sum of masses due to small contributions of a large number of the lowest modes. Usually, this is caused by local character of the lowest modes. The Seismic and Pseudo modes are presented to improve the situation of such difficult problems. The effectiveness of such approaches is illustrated by appendix 3C. Lanczos for direct solvers is available for these two modes. Modified Lanczos and PCG_Ritz are available for pseudo mode, when iterative solver is selected.

Modal

This mode constitutes a well-known approach implemented in the previous versions of Robot.

BLSI, SI, Lanczos and Basis Reduction Method for direct solvers and PCG method for iterative solver are available.

The convergence criteria for direct solvers are as follows. Iterations will stop when , where i = 1, 2, …, N; k - is the iteration number, N - number of modes (user defined ). The basis reduction method does not produce the convergence check, since it is not the iterative approach, although it is a kind of Ritz method. The number of master DOFs needs to be increased to improve the result precision.

The convergence criteria for PCG method (iterative solver) includes the following:

Details are described in appendix 3A.

Upper Limits is the lower bound value for period, frequency and pulsation. If this parameter is different from 0, all sequential eigenpairs from 0 to Upper Limit will be computed.

Mass% is the mass percentage (sum of masses for all computed modes for each direction).

Sturm check is a verification of skipped eigenpairs between 0 and shift parameter and consists in counting the negative elements on the diagonal of the decomposed shifted matrix

It is a very expensive procedure for large-scale problems. Let us take note that for seismic and spectral analysis it is unnecessary to get the continuous spectra of eigenvalues. It is important only to ensure the sufficient modal mass percentage for each direction. If such a condition is fulfilled, completeness of the basis is ensured. The implementation of BLSI allows one to produce the partial verification of continuity of eigenvalue spectra without running Sturm check. See the BLSI method description for more information.

Number of Modes	Upper Limits	Mass%	Program behavior
N	0 (inactive)	0 (inactive)	Sturm check is checked. Skipped frequencies for first N modes are missing. It is available for direct solvers when BLSI, SI or Lanczos methods are applied. It is not available for the basis reduction method and for all iterative solver methods. Define N first sequential eigenmodes. Sturm check is performed. If skipped frequencies are detected, a warning prompts the number of skipped frequencies. If instructed Yes, then iteration process is continued while the number of skipped eigenpairs is determined. Afterwards, Sturm check is repeated. No, then converged eigenpairs are saved as a final result and the next case is calculated Cancel, then iterations are continued while all skipped frequencies are determined. Warning is ignored. Sturm check is unchecked. Sturm check is not performed
N	ω ^*	Inactive (due to active Upper Limit)	Available only for direct solvers and BLSI, SI, and Lanczos methods. It is not available for the basis reduction method and all iterative solver methods. Sturm check is performed at the start of computations a the number of frequencies N1 which are contained between zero and Upper Limit is obtained: 0 < ω₁ < ω₂ < … < ω_N₁ < ω^* If (N1 > N), a warning prompts about the number of frequencies N1. If instructed Yes, compute 0 < ω₁ < ω₂ < … < ω_N₁ < ω^* No, stop computations. If (N1 <= N), compute 0 < ω₁ < ω₂ < … < ω_N₁ < ω^* without any warnings. In both cases it is possible to derive a number of converged eigenpairs higher than N1, but they will be saved as final results only when: 0 < ω₁ < ω₂ < … < ω_N₁ < ω^. All converged egenpairs that are larger than ω^, will be lost.
N	Inactive (due to active of mass%)	Active: 0< mass%<=100%	Available for all methods of direct solvers. It is not available for iterative solver. If mass% is not satisfactory, a relevant prompt is issued. No corrections are performed. Otherwise, computations are performed in the same manner as for the first case.

Number of Modes

Upper Limits

Mass%

Program behavior

(inactive)

Sturm check is checked. Skipped frequencies for first N modes are missing. It is available for direct solvers when BLSI, SI or Lanczos methods are applied. It is not available for the basis reduction method and for all iterative solver methods. Define N first sequential eigenmodes. Sturm check is performed. If skipped frequencies are detected, a warning prompts the number of skipped frequencies. If instructed

Yes, then iteration process is continued while the number of skipped eigenpairs is determined. Afterwards, Sturm check is repeated.

No, then converged eigenpairs are saved as a final result and the next case is calculated

Cancel, then iterations are continued while all skipped frequencies are determined. Warning is ignored.

Sturm check is unchecked. Sturm check is not performed

ω ^*

Inactive (due to active Upper Limit)

Available only for direct solvers and BLSI, SI, and Lanczos methods. It is not available for the basis reduction method and all iterative solver methods.

Sturm check is performed at the start of computations a the number of frequencies N1 which are contained between zero and Upper Limit is obtained:

0 < ω₁ < ω₂ < … < ω_N₁ < ω^*

If (N1 > N), a warning prompts about the number of frequencies N1. If instructed

Yes, compute 0 < ω₁ < ω₂ < … < ω_N₁ < ω^*

No, stop computations.
If (N1 <= N), compute 0 < ω₁ < ω₂ < … < ω_N₁ < ω^* without any warnings.

In both cases it is possible to derive a number of converged eigenpairs higher than N1, but they will be saved as final results only when: 0 < ω₁ < ω₂ < … < ω_N₁ < ω^*.

All converged egenpairs that are larger than ω^*, will be lost.

Inactive (due to active of mass%)

Active:

0< mass%<=100%

Available for all methods of direct solvers. It is not available for iterative solver. If mass% is not satisfactory, a relevant prompt is issued. No corrections are performed. Otherwise, computations are performed in the same manner as for the first case.

Seismic

This mode is available only for skyline or sparse direct solvers.

In seismic and spectral analysis, it is not important to use sequentially ordered eigenpairs since only the eigenpairs that contribute considerably to the seismic response (as they have significant mass participation factor) should be taken into account. Thus, the Sturm Check is not performed.

The Lanczos method usually ensures convergence of the number of eigenpairs considerably greater than N eigenpairs in the sequentially increasing order. When the skipped eigenvalues needs to be restored, it is necessary to get the number of converged frequencies considerably greater than the first N desired frequencies. For example, it is typical that the Lanczos method yields the following convergent frequencies.

When the user requires the sequentially ordered eigenpairs, he will obtain only the first 10 ones. The last 4 eigenpairs are simply thrown away, as well as the correspondence mass contribution. The essence of the proposed "Seismic" mode is to take all converged eigenpairs into account (not only the first sequential ones). It ensures a bigger sum of masses compared to "Modal" mode.

Available methods: Lanczos Method.

Upper Limits are ignored.

The current mass percentage is an average value of M%x, M%y, M%z for 3-D problems and a minimum value of M%x, M%z for 2-d problems (M%x, M%y, M%z are the current sum of masses for x, y, z direction, respectively). This strategy is explained by the fact that it is usually very difficult to ensure sufficient mass percentage for vertical direction. You can verify the mass percentage for each direction in the final results.

Nmodes	Upper Limits	Mass%	Program behavior
N	Inactive	Inactive (0)	Compute the N unsequenced eigenpairs. Sturm check is not performed. The number of converged eigenpairs equals N.
N	Inactive	Active: 0< mass%<= 100%	N is ignored. Computations continue until the current mass percent is not smaller than the demanded mass%, or the user is prompted to stop the computations, or the number of converged eigenpairs achieves the maximum available value. This value set is defined internally and it is 100 in the current version. After each 20 Lanczos steps, the number of the converged eigenpairs is recalculated and the current mass percentage is modified. A warning prompts the achieved mass percent. If instructed Yes, continue computations during the next 20 Lanczos steps and display this message again. If required mass percentage is not achieved (the number of converged eigenpairs does not exceed the maximum available value) No, save the converged eigenpairs as final results and pass them to the next case. Cancel, ignore all warnings in the future and continue computations.

Nmodes

Upper Limits

Mass%

Program behavior

Inactive

(0)

Compute the N unsequenced eigenpairs. Sturm check is not performed. The number of converged eigenpairs equals N.

Inactive

Active:

0< mass%<= 100%

N is ignored. Computations continue until the current mass percent is not smaller than the demanded mass%, or the user is prompted to stop the computations, or the number of converged eigenpairs achieves the maximum available value. This value set is defined internally and it is 100 in the current version.

After each 20 Lanczos steps, the number of the converged eigenpairs is recalculated and the current mass percentage is modified. A warning prompts the achieved mass percent. If instructed

Yes, continue computations during the next 20 Lanczos steps and display this message again. If required mass percentage is not achieved (the number of converged eigenpairs does not exceed the maximum available value)

No, save the converged eigenpairs as final results and pass them to the next case.

Cancel, ignore all warnings in the future and continue computations.

Pseudo

This mode is available for both the direct and iterative solvers. It is recommended only for seismic and spectral analysis when Modal and Seismic modes are too time consuming. The Modal and Seismic modes use eigenmodes as basis vectors for presenting seismic response and it is possible to require a very large number of eigenmodes to ensure a sufficient sum of masses for some difficult problems. Pseudo mode rejects this idea and generates the Ritz approximations to the lowest eigenpairs by means of Lanczos vectors for direct solvers or the Ritz-gradient [8] and modified Lanczos methods for iterative solvers. This is a more effective way of operation in most cases because a smaller number of basis vectors is required than in Modal. This was shown by E.L.Wilson [1-3]. Pseudo mode is similar to the Load dependent Ritz vectors, proposed in [1-3] and applied in SAP2000. It should be noted that the French code PS-92 admits the application of scientifically-based approaches to add systems of basis vectors to the existing eigenmodes in order to increase the sum of masses. The details of pseudo mode approach and it effectiveness are presented in appendices 3B and 3C, respectively.

Upper Limits are ignored.

The current mass percentage is defined as an average value of M%x, M%y, M%z for 3-D problems and as a minimum value of M%x, M%z for 2-d problems (M%x, M%y, M%z are the current sum of masses for x,y,z direction, respectively). This strategy is explained by the fact that it is usually very difficult to ensure sufficient mass percentage for vertical direction. You can verify the mass percentage for each direction in the final results.

Nmodes	Upper Limits	Mass%	Program behavior
N	inactive	Inactive (0)	Available for both direct and iterative solvers. Generate N basis vectors to define the work subspace. Save N basis vectors for use with seismic and spectral analyses. This regime is recommended.
N	Inactive	Active: 0< mass%<= 100%	Available only for direct solvers Generate N basis vectors to define the work subspace. Save these basis vectors which suffice to satisfy the given mass%. The number of saved basis vectors is less than N, if mass% < 100%

Nmodes

Upper Limits

Mass%

Program behavior

inactive

Inactive

(0)

Available for both direct and iterative solvers.

Generate N basis vectors to define the work subspace. Save N basis vectors for use with seismic and spectral analyses.

This regime is recommended.

Inactive

Active:

0< mass%<= 100%

Available only for direct solvers

Generate N basis vectors to define the work subspace. Save these basis vectors which suffice to satisfy the given mass%. The number of saved basis vectors is less than N,

if mass% < 100%

3.6. Spectral Analysis

The Response Spectra Method is applied for seismic and spectral analysis. This method consists in decomposing a structure of multiple degrees of freedom (MDOF) into a system of the single-degree of freedom (SDOF) oscillators. The response for each of these independent oscillators and the statistical summation of the extreme responses for each oscillator is calculated by means of SRSS, CQC, ten percent and double sum methods [3, 21].

The eigenmodes define this system of SDOF oscillators, when Modal or Seismic modes are applied. The pseudo mode basis vectors define this system of SDOF oscillators when Pseudo mode is applied (see section 3.5).

The introduction of the pseudo mode requires a new approach towards response evaluation for each mode. The classic approach is as follows:

( 3.1.1 )

where K, M - stiffness and mass matrices, Γ - mass participation factor, S_a - spectra acceleration, T - period, i - mode number, k - coefficient of spectrum scaling, dir - index of input seismic motion direction (dir = X,Y,Z), x - displacement vector for maximum reaction of i-mode.

Now, the following is applied (see appendix B):

( 3.1.2 )

where denotes a basis vector (it is not necessary for to be be an exact approximation of - exact eigenvector of , ω_i - approximation of exact eigenvalue Ωi. It is possible to show that (3.1.1) gives exactly the same solution as (3.1.2), if ( ωi = Ωi). However, (3.1.2) is applicable not only for direct solvers, but also for iterative solver, since it does not require the resolution procedure corresponding to the stiffness matrix K. This way is faster than (3.1.1) and allows one to control results more safely (sum of forces - sum of reactions).

The below-presented formula is obtained from (3.1.1)

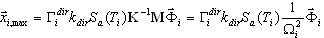( 3.1.3 )

The modal response vector describes the extreme response of the correspondence SDOF oscillator. The next step should be dedicated to defining the final response of the MDOF structure by means of statistic averaging between modes and between seismic input directions.

Earlier versions of Robot allows one to assign several statistically independent seismic input directions with their own scale multipliers in one load case. The statistical averaging between directions is produced by means of the sum of absolute values and the square root of the sum of squares combinations within each mode. The corresponding options are defined in Job Preferences.

The "sum of absolute values" option gives the following:

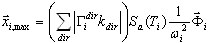( 3.1.4 )

The square root of the sum of squares option makes averaging of the of corresponding seismic input motion directions like .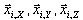

( 3.1.5 )

It is possible to show that each component of is the SRSS combination of correspondence components of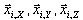

where i =1,2,…,N indicates the number of mode or pseudo mode.

The SRSS or CQC combination between modes (or pseudo modes) is applied to obtain the final response of the considered MDOF structure after the averaged modal response vectors have been obtained, i =1,2,…,N.

The modal averaged response vectors , i =1,2,…,N are the same for "sum of absolute values" and the square root of the sum of squares options if the single seismic input direction has been defined for the current load case (For example, Kx=Kz=0, Ky=1).

Robot (version 12.2 and later) saves the above-mentioned procedure of averaging modal responses between seismic input directions, however, it allows one to carry out the best approach. It is recommended to define a single seismic input direction for each load case, and then to apply either the SRSS combination between directions (corresponding to the American Regulatory Guides) or the so-called "Newmark" combinations (corresponding to the French seismic code PS-92 and the Eurocode-8).

Let us illustrate new capabilities of the following typical example.

In this case (single seismic input motion for each load case), the typical values for scale multipliers will equal

Kx=1; Ky=Kz=0 for dir = X (load case S_X)

Kx=0; Ky=1; Kz=0 for dir = Y (load case S_Y)

Kx=Ky=0; Kz=0.7 for dir = Z (load case S_Z; the vertical motion intensity is assumed to equal 2/3 of the horizontal motion intensity)

Three load cases are defined for each statistically independent seismic input motion. The modal response for each will be the same as (3.1.2) (i = 1,2,…,N; dir = X,Y,Z ).

Then, it is necessary to define the averaging factor over all modes due to each seismic input direction:

where - some factor (displacement, force, stress,…) for the i-th mode due to seismic input motion into direction dir which corresponds to the modal response (obtained from (3.1.2));

Rdir is the result of SRSS or CQC combination over all considered modes (pseudo modes).

Then, averaging over all active seismic input directions according to the chosen option is produced.

Either SRSS combination:

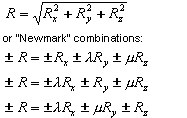
The Spectral Analysis options enable definition of arbitrary spectrum of seismic input motion.

3.7. Seismic Analysis

The Response Spectra Method is applied for seismic and spectral analysis. The seismic analysis is run on the basis of spectral analysis (see section 3.6), however, the spectra accelerations Sa = Sa(Ti) are generated to correspond to a selected seismic code, instead of being assigned by the user (as it is done for spectral analysis).

The UBC-97 seismic code is available in Robot (version 12.0 and the later ones). The Response Spectrum Analysis is run in accordance with Sections 1631.5.1 - 1631.5.3 of the 1997 Uniform Building Code. It is possible to fulfill the requirements of Section 1631.5.4 ("Elastic Response Parameters may be reduced …") by means of combination mechanisms of Robot. The basic shear components Vx, Vy, Vz, overturning moment components Mx, and My and torsion moment Mz (it is assumed that axis OZ is vertical) - all are presented in the "Reactions" table in the line "sum of forces", both for each modal response and for SRSS and CQC combinations between modes.

The following seismic codes are available in the program:

UBC97
PS 69 R. 82
AFPS
PS 92
RPA 88
DM 16.1.96
EC 8
IBC 2000
P100 92
Turkish code
Chinese codes
Argentinian code
EAK 2000.

3.8. Selective Filters

Only the modes that have a relatively significant mass participation factor make considerable contributions to the seismic response of a structure. Therefore, it suffices to take only these modes into account. The remaining modes with small mass participation factors can be ignored during seismic analysis. The number of derived modes is usually considerably greater than the number resulting from mass percentage assessment. Thus, the disk space and computation time may be saved, if only the modes with significant mass participation factors are selected.

Two methods can be used.

Create a list of accepted modes for each seismic input direction (seismic case) on the base of previously obtained results from modal analysis
Assign a mass limit bound value for modal mass percentage (all modes with modal mass percentage below that limit will be ignored).

The first way is more efficient, although it requires a previous modal analysis. The second way allows filters to be applied in the same run with spectral and seismic analysis, however, it usually occupies more disk space and involves greater computational effort.

Consider another example. The results of modal analysis are presented below, in table 3.1, where the seismic cases are defined in the following manner: Dir_X (Kx=1; Ky=Kz=0), Dir_Y (Kx=0; Ky=1; Kz=0) and Dir_Z (Kx=Ky=0; Kz=1)

Table 1

Mode number	Mass particip. UX (%)	Mass particip. UY (%)	Mass particip. UZ (%)	Period
1	0.05	12.01	0.004	0.803
2	67.43	0.06	0.005	0.705
3	0.002	0.08	0.07	0.686
4	0.001	0.008	0.009	0.650
5	25.4	0.07	2.06	0.590
6	0.09	68.5	5.05	0.540
7	0.08	10.3	0.06	0.490
8	0.07	0.06	0.56	0.460
9	0.05	0.07	30.56	0.420
10	0.08	0.06	0.25	0.380
11	0.06	0.01	26.7	0.270

Let us assume that we take all modes with mass participation factor greater than one percent into account. The corresponding mass participation values are given in the table. Let us take note that if seismic input directions are assigned as ( 1 0 0) for Seism_X case, the modes with significant mass participation values for directions UY, UZ do not contribute to seismic response at all (see section 3.6):

where dir = X, Y, Z - input seismic direction; 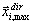-maximum response for i -mode; - mass participation factor; Sa(Ti) - spectra acceleration; - i-eigenvector or basis vector (in case of the pseudo mode). The scalar multiplier on the right side of the above formula defines the contribution of i-mode to the seismic response of dir direction. In this case, where Ky = Kz = 0, considerable contributions will be made by modes 2 and 5. The remaining modes do not contribute to seismic response, due to zero Kdir multiplier (dir = Y, Z) and to small mass participation values for dir=X direction. It is possible to show - in the same way - that for case Dir_Y it suffices to take the modes 1, 6, 7 into account, while for case Dir_Z - the modes: 5, 6, 9, 11.

Thus, by means of filters, the program may take only the relevant modes into account - 2 for Dir_X case, 3 for Dir_Y case and 4 for Dir_Z case. This occurs without a significant loss of mass contributions. Let us take note that we would be forced to apply the 11 modes for each case if we do not use the filters.

This approach enables reduced computation time for large-scale dynamic problems (as well as disk space requirements and the amount of data to be post-processed) without significant reduction of the result precision compared to the traditional method (when the selective filters are not used).

For example, the large-scale problem PJG203 contains 34 266 equations (bandwidth equals 990 after optimization). The corresponding FE model is presented in appendix 3D - see Fig.A1. The 25 eigenpairs with the consistent mass matrix and 3 seismic cases were to be calculated. The computation time still reaches approximately 50 hours on a Pentium PRO (64 MB RAM, 200MHZ). The required disk space exceeded 1GB. Moreover, there arose a problem with steel design module, caused by insufficient disk space. (To compute the SRSS and CQC combinations, it was necessary to store the data of 25 modes multiplied by 3 seismic cases comprising a large number of degrees of freedom for all factors - displacements, internal forces, stresses). Application of selective filters allows the program to solve this problem successfully.

3.9. Harmonic Analysis

The following definition of steady reaction of a structure to the action of a single - harmonic load is produced:

F(t) = F sin( ωt)

where w is the pulsation of the excitation load. The behavior of a structure is described as

(K - ω² M) X = F,

where X - amplitude value of the displacement vector.

3.10. Time-History Analysis

The modal decomposition (superposition) method is realized in Robot. It is based on the representation of a structure movement as a superposition of the movement of uncoupled modes. Therefore, the method requires the eigenvalues and eigenvectors to be determined. The Lanczos method is recommended for this purpose. The method of modal decomposition takes advantage of reduced uncoupled equations. It is an appropriate approach to analyze the dynamic response of structures subjected to long-term action of dynamic loads (for example, non-steady loading caused by working in-line equipment or seismic action). Mathematical background and particularities of application are presented in [3,4,6].

The equation (without damping) may take the following form:

(3.11.1)

where Ng - number of "load groups", φ_k(t) - given time history for the k-th load group.

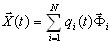(3.11.2)

where 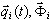- correspondingly i-th normal co-ordinate and mode (eigenvector or Ritz vector). Substitution (3.11.2) to (3.11.1) and addition of damping terms leads to the following uncoupled modal equations [3,4,6]

(3.11.3)

where , ξi - modal damping parameter (usually ξi = 0.05 - 0.2; when ξi = 1 it indicates critical damping - limit between oscillation motion and aperiodic motion), ωi - natural vibration frequency (pulsation), i=1,2,…,N

Each of the equations is solved numerically. Second-order method with automatic selection of integration step is applied. The resultant displacement vector for the defined time points t = t1, t2, …, t5 is obtained by means of substitution of qi(t5) in (3.11.2).

Modal decomposition method can be applied for analysis of seismic response. In such a case equation of motion takes the following form

and appropriate uncoupled modal equations -

(3.11.5)

where - mass participation factor for i-th mode and seismic input direction dir. Each mode must be normalized as follows: 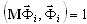. Finally all results (displacements, velocities, accelerations, internal forces, reactions, and others) are stored only for the defined time points t = t1, t2, …, t5. The high-performance post-processor allows one to analyze time-history analysis result both in the diagram and table modes. The diagram mode displays selected factors (displacement, acceleration, velocity, reactions, shear forces, bending moments, and others) for chosen degrees of freedom (DOF) and presents the deformed shape of a structure in the selected the time point. The table mode allows one not only to see the corresponding values, but also to search automatically the maximum and minimum values among the response factors over all stored time points.

3.11. Modal Analysis Taking Static Forces into Account

Linear small vibrations with respect to the equilibrium static state induced by a given static load is considered. The static forces are known to have influence on the natural vibration frequencies. The usual Modal Analysis does not take such influence into consideration, however, it does when Modal Analysis takes static forces into account.

Full non-linear equations describe the motion of the relatively static equilibrium state of a system, induced by the given static loads.

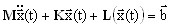(3.12.1)

where M, K - mass and stiffness matrices, L(x(t)) - non-linear operator, x(t), b - displacement vector and load vector. Linearization procedure consists of the following:

(3.12.2)

where x_st is a part of the common solution which describes the static equilibrium state and x_d (t) is a vector of small dynamic displacements. Non-linear operator can be presented as decomposition of Taylor('s) series

(3.12.3)

where 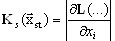is a stress-stiffness matrix, which is a Jacobian and takes the action of static forces into account. Thus, the following yields:

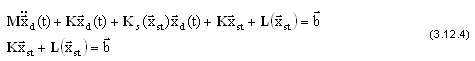
The first expression is a result of linearization of appropriately small dynamic displacements (note: ) and the second describes the non-linear static equilibrium state. Therefore, small dynamic motion with respect to the static equilibrium state is as follows:

(3.12.5)

Let us substitute x_d (t) = Φ e^{i ω t}. An eigenvalue problem originates from (3.12.5)

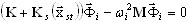(3.12.6)

where ω_i - eigenvalue; Φ_i - eigenvector.

The computations are performed in two stages:

Linear (3.12.7) or non-linear (3.12.8) analysis of static stress-strain state induced by a given static load
K x_st = b (3.12.7)

K x_st + L(x_st ) = b, (3.11.8)

where x_st - unknown vector of static state, b - vector of given static forces (static load vector), K - stiffness matrix, L (x_st , b) - non-linear operator. The static load vector b may be a result of the combination of several static loads. It should be noted here that a linear approach does not satisfy exactly the non-linear equilibrium equation (3.11.8). Thus, vector x_st for the static equilibrium state is a result of an approximate solution and the stress-stiffness matrix K_s(x_st ) contains an error. If the considered structure is sufficiently stiff and non-linear effects appear poorly, such approximation seems to be correct. Otherwise, it is necessary to solve the non-linear static problem (3.11.8) (that technique is not covered by the manual). Obviously, the linear approach (3.2.17) is faster than the non-linear one (3.11.8). In case of the linear approach, it turns out that K_s(x_st ) = G (x_st )= G, where G is a geometrical stiffness matrix.
Eigenvalue analysis (3.12.6)
The positive values of ωi (ωi > 0) are known to represent to stable equilibrium states, negative values (ωi < 0) - unstable ones, whereas zero value (ωi =0) corresponds to lack of stability (buckling).

The loss of positive definiteness of matrix K + K_s(x_st ) means that static load exceeds its critical (buckling) value. A relevant warning is issued. The convergence will be lost during the run of non-linear static problem (3.11.8). It is recommended to interrupt computations because the following calculations are still senseless.

Only the non-linear approach is available for structures containing cable and tension-compression elements.

For example, let us consider the following figure.

Fig. 3.11.1

There is N - static load. The following expression describes behavior of such a system:

( 3.11.9 )

where: w - bending displacement, ρ - material density, F - cross-section area.

The solution will be searched as

( 3.11.10 )

After substitution ( 3.11.10 ) to ( 3.11.9) the following is derived:

, ( 3.11.11 )

where - buckling load, ω₀ - eigenvalue for N = 0 (result of usual Modal Analysis). Finally,

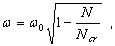( 3.11.12 )

where ω - eigenvalue for the system subjected to action of a static load N. This result is presented graphically in Fig. 3.11.2:

Fig.3.11.2

The dependence ω = ω (λ), where l is a load parameter, for a real structure is usually more complex than presented by the expression ( 3.11.12 ) (see [ 1,22 ]).

Appendix 3A

Eigenproblem Solution Methods

Understand that the best universal method of solving an eigenproblem does not presently exist.

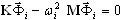, i=1,2,…,n ( A1 )

where K is the stiffness matrix, M is the mass matrix, is the eigenmode and ω_i is the pulsation. For most of the problems such a method will use up less resources (the computation time and HD storage) than any other. However, it does not exclude different situations in case of other tasks. Application of another method is recommended. The present version of Robot covers several methods of solving a generalized eigenproblem (A1). Each of them involves its own advantages and disadvantages. Below, we present some recommendations to be considered while choosing an analysis method. We hope that, in the majority of cases, they will lead to the required results in the best way.

The subspace iteration (SI) method is realized exactly as described in [4], therefore, the description of this method is not included here.

Lanczos

The Lanczos method [12,16,17] is a powerful robust approach used for solving large-scale eigenvalue problems (A1). It is available when skyline or sparse direct solvers are selected.

This approach finds the required first n eigenvalues and eigenmodes with any desired precision. The greater number of the required eigenpairs is obtained, the more significantly advantageous the Lanczos method becomes. However, the approach involves several limitations.

The three-diagonal matrix T should not be decomposed. It is impossible to analyze a structure which consists of two or more unconnected substructures. In such a case, each substructure is considered separately, or another approach is implemented (for example, block subspace iteration (BLSI) or the basis reduction methods).

The mass matrix M should be taken as Lumped with Rotations or Consistent.

Zero density is not allowable.

The Lanczos Method uses reduction to the three-diagonal matrix T

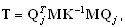, ( A2 )

where Q_j = {q1, q2, …, qj} - the rectangular matrix Neq x j, and Neq is the number of equations, j - number of "Lanczos" steps, qj - j-th Lanczos vector. The expression

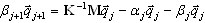( A3 )

generates the next Lanczos vector qj+1, and defines the current line of T matrix

Thus, the following reduced eigenproblem is obtained:

, k=1,2,…,j ( A4 )

is the j-th approximation to ω_k, k=1,2,…,n, n is the required number of eigenpairs. The algorithm will continue computations (to increase the j - number of Lanczos steps), until the required accuracy is achieved for all required eigenvalues.

The selective orthogonalization procedure supports the required level of orthogonality between Lanczos vectors qj which ensures safety and numerical stability of the computational process. We employ economic methods to provide selective orthogonalization and to solve the reduced eigenvalue problem (A4) by double QR-iterations with shifts.

The source eigenvectors are determined by the following formula

( A5 )

The details are presented in [12,16,17].

Basis Reduction Method

This method [4, 5] is known as the improved Rayleigh-Ritz method [4]. In [5] such a method a discrete variant of Bubnov-Galerkin method is presented. This algorithm allows one to get approximate values of the first few eigenpairs if the some information about them is known. This method requires assigning a master degree of freedom (MDOF) in order to get the reduced system. Thus, the process of creating the reduced model can be controlled. It is a powerful tool for those experienced in dynamic analysis of structures and deal with the same type of structures whose behavior is known. This method allows exclusion of undesirable degrees of freedom (DOF) from the reduced model and reduces the initial complex problem with a large number of DOF to a reduced form. This is achieved with a considerably smaller number of DOF. The experience concerning structure dynamic analysis shows that some problems can be encountered by the user when the automatic reduction methods (BLSI, SI and Lanczos are taken into account) lead to a very complex computation process. For example, the local vibration modes of single bars can lead to serious problems since the computation process seeks the eigenpairs automatically without any selection. It should be noted that for the majority of cases in real structures. Otherwise, these local vibrations will be restricted by some constraints not taken into account in the FEM model, or their contribution will be inessential to the overall system motion. Usually, the mass percentage is very small for such local vibrations. The usage of exact methods in this case will lead to the above-mentioned difficulties. However, the implementation of the approximate basis reduction method can simplify the computation process considerably.

This method has the following limitations.

The user has to assign the MDOF: the master nodes and master directions. It is assumed that only displacements (not rotations) may be assigned as the master degrees of freedom.

The algorithm is implemented for any type of mass matrix; however, Lumped without rotations mass matrix type is most advantageous with respect to computation time.

The Sturm sequence check is not available. There is only one way to check convergence. Increase the number of MDOF (assign additional master nodes and master directions), solve this problem once more, and compare the eigenvalues.

Such a method transforms the source large-scale eigenvalue problem for FEM

(A6)

model (A1) into eigenvalue problem for reduced model

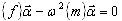(A7)

where {f} - the influence matrix, {m} - the generalized mass matrix for a reduced model,

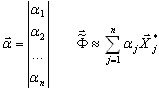(A8)

Where n is a number of degrees of freedom of a reduced model. The basis for such transformations is a static solution obtained for appropriate unit states: unit nodal forces are applied consequently in each master node, in the selected master direction. A large-scale static problem is solved for n right-hand sides:

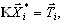i = 1, 2, …, n (A9)

where Ti - load vector which corresponds to i - unit load. The user has to assign master nodes and master directions. All demanded operations will be performed by the program.

The reduced eigenvalue problem is solved by Jacobi method, which leads to the approximate frequencies ω_i, and modes , i=1,2,…,n. The details of this approach are presented in [5].

Block Subspace Iteration Method

The block subspace iteration method (BLSI) solves a generalized eigenvalue problem (A1). It is available for skyline and sparse direct solvers. It is a powerful robust approach. Application of this method is strongly recommended when a large-scale problem arises and it is necessary to obtain a large number of eigenpairs (more than 10). BLSI can be applied for analysis of separate structures. All types of mass matrices (Lumped without rotations, Lumped with rotations and Consistent) during modal analysis are available. The application area of this approach is limited by the modal mode. The seismic and pseudo modes are still available if Lanczos is chosen.

The Sturm sequence check is performed to detect the skipped eigenvalues. BLSI controls the continuity of converged eigenvalues. Discontinuity of converged eigenvalues indicates the presence of skipped eigenvalues. However, continuity of converged eigenvalues does not provide a strict assurance that skipped eigenvalues are missing. Nevertheless, results of numerous computations indicate that in most cases, Sturm sequence checks do not detect skipped eigenvalues when BLSI ensures the continuity of convergence. The great advantage of this method is the possibility of avoiding the time-consuming Sturm check procedure if a full warrant of missing skipped eigenvalues is not needed. If discontinuity of converged eigenvalues is met, the following message appears (see Fig A1).

The main idea of BLSI method [1-3] consists in simultaneous vector iterations in the subspace of the fixed size. Each converged vector is removed from work subspace (block) and instead of it a new start vector is added. The orthogonality of the converged vectors is ensured on each iteration step.

Application of the shift acceleration procedure [1,4] is recommended during modal analysis when slow convergence occurs.

, ( A10 )

where K_σ= K - σ M, σ - shift value. At the beginning of analysis σ = 0 is assumed. The automatic update of shift value is made, if new converged eigenvalues do not appear through the accepted number of control iteration steps. For example, let us accept the number of control steps equal to 5. Then 5 converged eigenvalues appear after 4 iterations. The shift value remains σ = 0. On the next iteration step 3 eigenvalues converge. The shift value remains σ = 0. Then, throughout 5 iteration steps no eigenmodes converge. The algorithm detects "slow convergence" again, adopts σ = ω₈ ², updatesK_σ = K - σ M and factorizes the updated shifted matrix K_σ. Then after 2 iteration steps converge 2 eigenmodes. The shift value remains ω₈ ². Then during following 5 iteration steps do not converge any eigenvalues. The algorithm again detects a "slow convergence" and takes ω₁₀ ² , updates K_σ = K - σ M and factorize updated shifted matrix K_σ.

Fig. A1 Discontinuity of converged eigenvalues is detected while running BLSI.

If instructed:

Yes, computations will be continued until the next converged eigenvalue appears. Afterward, the next verification will be perfomed.
No, results will be saved and computations will proceed to the next case.
Cancel, computations continue as long as the full continuity of converged eigenvalues is ensured. Warning will be ignored.

These are not all the recommendations. You can either apply or not apply the shift accelerations. Remember, application of the appropriate shift is a powerful tool of convergence acceleration. Otherwise, each factorization of the updated K_σ matrix may be a time-consuming procedure, especially for a large-scale problem. Thus, the final decision about shift application should be made on the basis of experience and intuition of the user.

The following example illustrates the benefit of shift application. The computation model is shown in Fig.A2. There are 50 eigenmodes extracted by BLSI. Solver skyline is selected. Tolerance 1.0e-09 is accepted. It turns out that convergence beginning with 38 mode is still so slow that for 20 minutes of computations no results are obtained. Once shift acceleration (update of a shift was accepted over each of the 5 unconverted iteration steps) has been activated, computation time still amounts to 50 seconds. Obviously, it is possible to present numerous examples, when application of shift reduces the number of iterations; however, it increases the computation time. We recommend activation of shift accelerations when a conventional approach (shifts are turned off) leads to a large number of iterations at some stages of the BLSI run.

Fig.A2 Spatial frame structure

Modified Lanczos Method

This is an adjustment of the Lanczos method in pseudo mode to iterative solver. Usual Lanczos requires factorization of a stiffness matrix (see A3). When a large-scale problem is met, factorization of the stiffness matrix is still very time-consuming. In case of large problems (over 100,000 equations), not only does factorization of a stiffness matrix require enormous computational effort, but the solution of an equation set of appropriately factorized matrix is also expensive.

The modified Lanczos method is based on the iterative approach. It avoids storage, assembling and factorization of a large-scale stiffness matrix. Evaluation of each Lanczos vector requires approximately as much computational effort as the solution of a static problem with a single right-hand side. In regards to the pseudo mode, it reduces the required number of Lanczos vectors compared to Modal which is applied when running the modified Lanczos method.

Iterative solver AEBEIS (see [7,8]) is applied for the generation of Lanczos vectors. It is recommended to use the ICCF (incomplete Cholesky factorization) technique for both multilevel aggregation preconditioning [7,8,18-20] and the usual non-multilevel. It ensures fast operations during matrix-vector product evaluations and fast resolution of correspondence preconditioning. It should be noted that the tolerance adopted for the iterative solver (Job preferences > Structure Analysis > Parameters) determines the precision of evaluation of Lanczos vectors. Usually it is sufficient to accept 1.0e-04. The greater Number of Modes will be taken into account, the closer low Ritz vectors will be to the corresponding eigenmodes, and a fuller sum of modal masses will be achieved.

Preconditioned Conjugate Gradient Method (PCG)

PCG method [9-13] is recommended for the definition of a small number of eigenmodes in the modal mode when iterative solver is applied. It may prove very useful for assigning a wind load or for checking a few low modes obtained by PCG_Ritz method. All types of preconditioning (see Tools > Job Preferences > Iterative > Parameters) defined for static analysis, are available. All types of mass matrix (consistent, lumped with rotations, and lumped without rotations) can be used.

A preconditioned conjugate gradient method is based on direct minimization of Rayleigh quotient

(A11)

by means of the gradient approach where: k - number of iteration, λ_k - corresponding approximation of an eigenvalue. The gradient approach searches such value of parameter α_k which ensures the minimum value of λk from (A11):

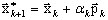(A12)

where p_k is a vector of conjugate direction. Search of the appropriate value of α_k [see 9-13] leads to:

Preconditioning B is applied to accelerate the convergence

B z_k+1 = r_k+1 -> z_k+1 (A13)

Gradient direction is defined as

(A14)

New conjugate direction is defined as

(A15)

where

Iterations are performed until

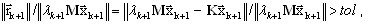(A16)

where tol is a desired tolerance. Usually tol = 1.0e-02 ensures very good precision for engineering purposes. It should be remembered, that the convergence ratio (A16) is computed in very strong norm (see the part covering precision of computations). The tolerance mentioned above provides precision of eigenvalues not worse than 1.0e-04.

When a first eigenpair is converged, it is stored as a final result, and iterations begin to compute the next one. The orthogonalization procedure of the previously defined eigenvectors on each iteration step is employed to avoid doubling of eigenpairs. Such process is applied until all desired eigenpairs are obtained.

The most efficient way of convergence acceleration for PCG is the implementation of good preconditioning. All types of preconditioning presented for an iterative solver are available for PCG method. It is strictly recommended to apply the multilevel preconditioning [18-20] or non-multilevel preconditioning with ICCF [9-12] smoothing from AEBEIS solver [7,8].

Ritz-gradient Method (PCG_Ritz)

PCG_Ritz method [8] is a fast method of definition of a set of Ritz vectors in pseudo mode when iterative solver is selected. Such an approach may be very fruitful for seismic and spectral analysis of medium-size structures including (10,000 - 60,000) equations.

It is based on the generation of the orthogonal system of basis vectors. The gradient approach with multilevel aggregation preconditioning on the basis of element-by-element technique is applied to minimize the Rayleigh quotient for each step of basis vector preparation. It ensures evolution of the consequence basis vector toward the lowest eigenmode without aggregation and decomposition of a large-scale stiffness matrix. Such a method is often more effective for dynamic response analysis compared to classic modal superposition method, especially for seismic response analysis. The proposed method allows one to apply arbitrary types of finite elements due to aggregation approach and ensures a fast solution and an inexpensive requirement concerning disk storage, caused by using EBE. This method is particularly effective when the consistent mass matrix is used.

The given eigenvalue problem is as follows:

Kφ - λM φ = 0 (A17)

where K, M are the stiffness and mass matrices respectively, φ is the eigevector and λ is the eigenvalue. The procedure of evolution of the basis vector's set x0, x1, …, xn toward the lowest eigenmode will be described. The preconditioned gradient approach is applied to minimize the Rayleigh quotient

(A18)

where 0 ≤ k ≤ n, k is the evolution step number; n+1 is the number of basis vectors, which define the size of the subspace span belonging to (x0, x1, …, xn); n+1 << N, where N is the number of degrees of freedom for the considered problem (A17). It very often appears that the considered eigenvalue problem is ill-conditioned. In such a case the evolution of the consequence basis vector xk toward the lowest eigenmode will be very slow. The preconditioning operator B is applied to improve such a situation. The expression B z_k = r_k -> z_k denotes the resolution of a given equation set of correspondence vector zk, where B is a preconditioning operator and r_k = Kx _k - λ_k M x_k is a corresponding residual vector.

The basis vectors satisfy the following conditions of orthogonality:

(A19)

The source large-scale eigenproblem (A17) is reduced to the subspace eigenproblem

(A20)

The matrices of subspace projection are defined as {k_ij} = {Kx_i, x_j} and {m_ij} = {Mx_i, x_j} = U, where U is a unit matrix.

The Ritz vectors v₁, v₂, …, v_n+1 for the derived basis vectors x0, x1, …, xn and the corresponding approximations of frequencies ω₁, ω₂, …, ω_n+1 are utilized for superposition of the structural dynamic response.

The procedure of the evolution of the basis vectors x_k, k = 0, 1, …, n toward the lowest eigenmode is very close to the corresponding step of preconditioned gradient iteration method for eigenproblem solution. It is a well-known fact that convergence of the preconditioned iteration methods depends considerably on the properties of the preconditioned operator B. This operator should be positively definite; it allows inexpensive solution B z_k+1 = r_k+1 and satisfies the condition number C ( B^-1 K) -> 1 in the best possible manner.

The last requirement in case of Ritz-gradient method ensures good approximation of the low part of eigenmodes.

Such a method is available only for the multilevel iterative approach, which ensures a good quality of preconditioning. Both EBE (element-by-element) preconditioning technique and ICCF technique one are used. The quality of Ritz vectors generated in such way depends considerably on the properties of the preconditioning operator B (see A13 and [8]). Since the coarse level model approximates well the low vibration modes, the Ritz vectors on the fine level are a good approximation of the corresponding eigenvectors (see [8]). Thus, the quality of results, obtained using such a method, depends considerably on the ability of the coarse level model to maintain similarity to the given FEM model (so-called fine level). Usually a single aggregation level ensures good approximation. When the number of aggregation levels is larger than one, quality of results is not guaranteed. It is a main limitation of this method application for analysis of a large-scale problem, when the number of equations exceeds ~60000.

If preconditioning matrix B = K (the coarse level is identical to the fine level), the proposed Ritz-gradient method passes exactly to Lanczos method (see [8]). Mathematical background is presented in [8].

Modal Analysis - Precision of Computations

The generalized eigenvalue problem is defined as

Kφ - λM φ = 0 (A17)

where K, M are the stiffness and mass matrices respectively, {φ, λ} - eigenpairs (natural vibration mode and eigenvalue). Two types of residual vectors are defined:

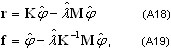
where {φ, λ} are really computed eigenpairs which contain some computational errors. The first expression defines the residual vector in terms of forces and the second one - in terms of displacements.

Four different criteria are used to estimate the computational error of eigenvectors.

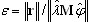. It is a very stiff criterion. Usually ε ≤ 0.01 means that first four digits in the eigenvalue are defined exactly. It is applied only for PCG, when iterative solver is selected.
e = (r, φ). It is a slightly softer criterion than the previous one. It is applied for modified Lanczos method, when iterative solver is selected.
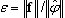. It is a soft criterion because convergence of displacements in given realization of FEM is usually faster than convergence of internal forces. It is used for BLSI, SI and Lanczos, when skyline or sparse direct solvers are selected.
·, where λk, λk-1 - two successive eigenvalues on k, k-1 iteration steps and tol denotes the tolerance for eigenvalues, adopted in the Modal Analysis Parameters dialog box. It is used as intermediate criterion while the following methods are being run: BLSI, SI and Lanczos (skyline or sparse direct solvers) in the modal mode. Such a criterion is not robust, however, it is very fast. The use of (4) allows one to reduce considerably computation time for BLSI, SI, Lanczos methods, especially for large-scale problems. When an eigenvalue analysis is completed, criterion (3) is applied as the final verification of precision. The user should look at the "Precision" column in the table where the value 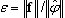is presented. If insufficient precision is met for an eigenmode, it is necessary to repeat the eigenvalue analysis with a higher tolerance for eigenvalues tol.

The following table summarizes the considerations mentioned above. The symbol N/A means that the corresponding convergence check is not produced. Results of the final verification are obtained only once and are presented in the "Precision" column of the table. The convergence check during computations is performed several times.

	Direct solvers	Iterative solver
Type of criterion	BLSI, SI, Lanczos method	Basis reduction method	Modified Lanczos	PCG_Ritz	PCG
During computations		N/A	N/A	N/A
Final verification		N/A	e = (r, j)	N/A

Direct solvers

Iterative solver

Type of criterion

BLSI,

SI,

Lanczos method

Basis reduction method

Modified Lanczos

PCG_Ritz

PCG

During computations

N/A

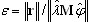
Final verification

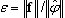
N/A

e = (r, j)

N/A

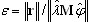
It should be noted, that Lanczos for seismic mode produces convergence check 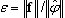through each of the 20 Lanczos steps. Basis reduction method and PCG_Ritz method are the Ritz methods. Since it is not the iterative approach, verification of precision is not performed.

If precision of some modes after computation appears to be insufficient, the following is necessary:

Direct solvers	Iterative solver
BLSI, SI, Lanczos method - modal mode	Basis reduction method	Modified Lanczos	PCG_Ritz	PCG
Decrease tol from Modal Analysis Parameters dialog box	Increase the number of basis nodes and basis directions	Increase the number of modes; Decrease the tol in Iterative Solver Parameters dialog box	Increase the number of modes; decrease the number of aggregation levels; increase the number of inner iterations	Decrease tol in Modal Analysis Parameters dialog box

Direct solvers

Iterative solver

BLSI,

SI,

Lanczos method - modal mode

Basis reduction method

Modified Lanczos

PCG_Ritz

PCG

Decrease tol from Modal Analysis Parameters dialog box

Increase the number of basis nodes and basis directions

Increase the number of modes;

Decrease the tol in Iterative Solver Parameters dialog box

Increase the number of modes;

decrease the number of aggregation levels;

increase the number of inner iterations

Decrease tol in Modal Analysis Parameters dialog box

Appendix 3B

The Pseudo Mode Approach

The source motion equations for seismic loads take the following form:

(B1)

K, M - the stiffness and mass matrices;

I dir - direction unit vector; φ(t) - time history of the ground acceleration

The solution is searched as:

(B2)

where q_i are the basis vectors of the size Neq - number of equations of the source FE model.

These vectors should satisfy the following requirements:

kinematics and static boundary conditions;
linear independence
basis completeness.

It is possible to adopt either Lanczos vectors or any vectors obtained for unit concentrated nodal forces (basis reduction method for direct solvers or Ritz-gradient PCG_Ritz method).

The subspace projection is described as:

Let us note that β is of the N size; the Q matrix is of the NeqxN size.

The subspace equations (B3) will be solved by means of decomposition of the eigenvectors (on the subspace which is defined by Q = {q1, q2, …, qN}).

Let us note that decomposition (4) is an exact expression, because the k subscript assumes values from 1 to N - over the entire size of subspace Q.

The substitution (B4) to (B3) leads to the uncoupled set of equations

Let us consider

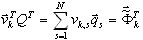(B6)

Thus, (B5) can be presented as

(B7)

where k=1,2,…,N.

Let us apply the response spectra method to the uncoupled equations (B7)

(B8)

where are the maximum response for k subspace mode and spectra acceleration function, respectively.

Let us substitute (B8) to (B4) and then to (B2):

(B9)

It should be noted that for N -> Neq:

ω_k -> Ω_k

where Ωk, are the exact eigenpair of the source FEs eigenproblem

(B10)

and 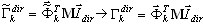where is the mass participation factor for k eigenmode.

Conclusions

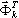The proposed approach does not require the "good" approximations , ω_k -> Ω_k. It is possible that , ω_k approximate the , Ω_k with arbitrary precision.
The proposed approach is not worse than the well-known modal decomposition (superposition) method. Both of these methods constitute particular cases of the common projection method and converge to the "exact" solution when N -> Neq. (This statement is not valid exactly for response spectra method, because this method is of the statistical character and its convergence to the exact solution takes place when N -> ∞. It is obvious that for N > Neq there will arise a computational conflict due to the fact that the number of basis vectors cannot exceed Neq . Therefore, it is possible to get different solutions for different basis vectors when N = Neq . It is a particularity of the response spectra method. For methods other than the response spectra method, the full convergence takes place when N = Neq. The convergence for the case of response spectra method should be considered in the statistical sense only, because this method constitutes a statistical approach aimed at getting an average solution once the time history has been lost. Due to that the term "exact solution" should be applied with caution).
Which basis is better: Ritz vectors or eigenvectors? There should be such a basis which will ensure better convergence to the "exact" solution (N = Neq) by means of the smallest number of basis functions N. The question should be solved by examining practical examples.
Usually, the first part of pairs , ω_k provide good approximations to the correspondence eigenpairs 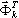, Ω_k (It is possible to determine the precision of each pair in the "Precision" column of the output listing). Only the last part of pairs , ω_k provide bad approximations to the exact eigenpairs and may be considered to be "pseudo modes" (from the viewpoint of the French seismic code PS-92).
The use of the entire subspace Q = {q1, q2, …, qN} ensures fast increase of mass percentage. In case of Modal and Seismic modes, only a part of this subspace is used.

Appendix 3C

The examples of application of the Seismic and Pseudo modes.

It is obvious that there are many kinds of seismic and spectral problems where it is difficult to get sufficient (70%- 90%) percentage of masses. It is possible to solve the so-called good problems using well-known methods.

Assign an arbitrary number of N modes.
Compute the first sequential N modes by means of the Modal mode.

However, for hard problems this approach may turn out to be unreachable. Let us consider, for example, the Coreal or Museum problems. They are FEM models which have been prepared by French engineers. A mass percentage for adifferent number of defined eigenmodes is presented. The Modal mode (Lanczos method) is used.

The convergence history for problem Coreal

Number of Converged Modes	Mass %
44	< 1%
62	12%
75	38%
89	60%
116	74%
154	77%
179	80%

The convergence history for problem Museum

Number of Converged Modes	Mass %
41	20%
106	40%
119	42%

For example, 80% means that for two directions sums of masses are not smaller than the given number. The Modal mode generates eigenmodes, while either the adopted mass percentage is achieved or the assigned top limit number of modes is exhausted. The final solution of the response spectra method is obtained in the form of statistical superposition of eigenvectors.

In both problems under consideration, the number of degrees of freedom is smaller than 2000. Such problems are considered to be small (with respect to the number of degrees of freedom). In the cases of medium-sized and large-scale (tough) problems, it is possible that both the Modal and Seismic modes remain inapplicable in practice due to the expansive character of the computation process. In such cases, application of the Pseudo mode is recommended. Below, the convergence history for Coreal and Museum problems is presented.

There "convergence history" for problem "Coreal"

Number of Basis Vectors	Mass %
10	58%
20	67%
40	70%
80	80%

There "convergence history" for problem "Museum"

Number of Basis Vectors	Mass %
10	60%
20	66%
40	71%

Note: It is necessary to define approximately 130 - 150 Lanczos vectors to obtain 80 eigenvectors for the Modal mode. The computational effort in Pseudo mode is considerably smaller (approximately 3 - 5 times).

The convergence of results in the Pseudo mode is illustrated in the next problem. The following table presents the resultant max/min values of CQC combination for the Modal and Pseudo modes.

Mode	UX (cm)	UY (cm)	UZ (cm)	Mass percent.
Modal	5.52002e-00	5. 88293e-00	5.83013e-00	81%
Pseudo, Nvect = 10	5.58710e-00	5. 89055e-00	5.00224e-00	80%
Pseudo, Nvect = 20	5.52937e-00	5.88870e-00	6.08661e-00	91%

Nvect - the number of basis vectors.

Appendix 3D

Application of Modal Analysis Methods to Solution of Large-scale Problems

Example 1

The comparison of computation time for BLSI and Lanczos methods. Different numbers of eigenmodes are considered.

Applied solver: sparse direct solver. Mass matrix type: Lumped with rotations.

Fig. D1. Model of a hotel. Number of nodes: 6 359; Number of elements: 7 264; Number of equations: 37 806.

Table D1. Result Comparison

BLSI		Lanczos
f (Hz)	Precision	F (Hz)	Precision
2,794e-001	1,082e-006	2,794e-001	5,680e-015
1,388e+000	1,389e-004	1,388e+000	2,199e-013
1,520e+000	7,847e-004	1,520e+000	8,193e-012
1,644e+000	2,469e-004	1,644e+000	4,497e-013
1,747e+000	2,691e-004	1,747e+000	5,455e-014
1,776e+000	3,092e-004	1,776e+000	9,127e-013
1,806e+000	3,153e-004	1,806e+000	6,621e-013
1,818e+000	6,383e-004	1,818e+000	3,656e-012
2,622e+000	1,565e-003	2,343e+000	2,047e-011
2,634e+000	1,383e-003	2,622e+000	1,223e-005

Since Sturm check is not performed, skipped eigenpair occurs between 8^th and 9^th modes, when BLSI is applied.

Table D2. Duration of mode extraction (in seconds)

Method	10 modes	50 modes	100 modes
BLSI	735	6029	23572
Lanczos	1472	12637	25271

Factorization of matrix: 841 s.

Advanced methods (BLSI, Lanczos) on the basis of powerful sparse direct solver quickly produces matrix factorization and extracts a large number of eigenmodes. Computations were performed on a P-350 (256 MB RAM) computer.

Example 2

Application of different methods to the solution of PJG203 problem. The model contains rigid links which leads to the use of a consistent mass matrix. 25 pseudo modes were extracted.

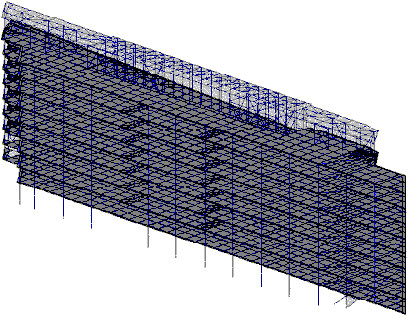
Fig. D2. PJG203 problem. Number of nodes: 5 945; number of element: 11 471; number of rigid links: 22; number of compatible nodes: 302; number of equations: 34 266.

Table D3. Computation time, disk storage, the first ten frequencies and corresponding precision for different methods.

Method	Time (s)	HDD (MB)	Frequencies (Hz)	Precision
Skyline	61 633	597	1.175e+000 1.337e+000 1.454e+000 2.445e+000 2.445e+000 2.628e+000 2.829e+000 3.033e+000 3.209e+000 3.595e+000	8.043e-015 1.025e-013 1.031e-013 1.712e-006 5.566e-006 6.331e-008 3.538e-001 3.052e-005 9.086e-005 4.498e-003
Sparse	4 435	99	1.175e+000 1.337e+000 1.454e+000 2.445e+000 2.445e+000 2.628e+000 2.825e+000 3.033e+000 3.209e+000 3.595e+000	3.522e-012 2.689e-011 1.159e-010 1.735e-006 5.639e-006 6.419e-008 3.520e-001 3.034e-005 9.938e-005 4.386e-003
Modif. Lanczos	3 459	24	1.175e+000 1.337e+000 1.454e+000 2.445e+000 2.445e+000 2.628e+000 2.791e+000 3.033e+000 3.209e+000 3.595e+000	3.719e-004 3.891e-004 6.601e-004 1.454e-003 1.875e-003 2.946e-003 3.364e-003 3.923e-003 2.175e-002 1.580e-001
PCG_Ritz	1 521	24	1.266e+000 1.350e+000 1.467e+000 2.445e+000 2.446e+000 2.446e+000 2.805e+000 3.035e+000 3.381e+000 3.566e+000	N/A - PCG_Ritz is not an iterative method, it is a Ritz method. Therefore, pseudo modes are obtained instead of the "exact" eigenmodes

The following parameters have been used for the modified Lanczos method: iterative solver AEBEIS (multilevel mode); ICCF preconditioning; 2 aggregation levels; 4 inner iterations, tol = 1.0e-04 - precision of generation of Lanczos vectors.

The following parameters have been adopted for PCG_Ritz method: iterative solver AEBEIS multilevel; ICCF preconditioning; 1 aggregation level; 4 inner iterations

The converged frequencies are marked in red. If the precision (see Appendix 3A) of a relative norm of a residual vector for a given mode is less than 5.0e-02, such a norm can be considered as fully converged to the corresponding eigenvector. Therefore, the frequencies marked in red are considered to be the exact values for a given discrete model. Error estimation for the PCG_Ritz method is presented in table D4. It can be concluded, that results obtained by PCG_Ritz method provide sufficiently good approximation for engineering purposes and such an approach can be used for fast estimation of seismic behavior.

The advanced methods allow one to drastically reduce computation time and disk storage requirements without any serious loss of correctness.

Table D4. Error estimation for PCG_Ritz method

"exact" frequency	PCG_Ritz results	Error (%)
1.175e+000	1.266e+000	7.7
1.337e+000	1.350e+000	1.0
1.454e+000	1.467e+000	0.9
2.445e+000	2.445e+000	0.0
2.445e+000	2.446e+000	0.0
2.628e+000	2.446e+000	7.0
2.791e+000	2.805e+000	0.5
3.033e+000	3.035e+000	0.1
3.209e+000	3.381e+000	5.4
3.595e+000	3.566e+000	0.8

Computations were performed on PC-450 (128 MB RAM) computer.

Example 3

A thin square plate with a consistent mass matrix clamped along one edge is considered. The 4-noded shell element and mesh 128x128 (number of equations Neq is 99072) are used. The 40 pseudo modes are extracted.

The computation time and disk space storage for Lanczos (skyline and sparse), modified Lanczos method (iterative solver) and Ritz-gradient (PCG_Ritz) methods are presented in table D5.

Table D5. Computation time and disk storage requirements for several methods.

Method	Time (s)	HDD (MB)
Lanczos, solver skyline	141 559	7 367
Lanczos, solver sparse	15 615	157
Modified Lanczos, iterative solver	18 978	0 - in core
PSG_Ritz	9 651	192

Computations were performed on PC-450 (128 MB RAM) computer.

the first ten frequencies obtained by Lanczos (skyline or sparse) and modified Lanczos (iterative solver, ICCF preconditioning, 3 aggregation levels, 8 inner iterations, tolerance 1.0e-03 for generation of Lanczos vectors were adopted) are identical. As the precision of computations was very high, it was possible to consider such values to be exact within the given discrete model. They are adopted as etalon values for error estimation for frequencies obtained by PCG_Ritz method. The multilevel approach with ICCF preconditioning (one aggregation level, 4 inner iterations) was selected when PCG_Ritz method was being applied. The corresponding results are presented in table D6.

Table D6. Comparison of frequencies for PCG_Ritz and Lanczos methods

Frequencies by Lanczos (Hz)	Precision	Frequencies by PCG_Ritz (Hz)	Error (%)
3.722e+000	5.918e-014	3.725e+000	0.08
9.112e+000	4.474e-014	9.115e+000	0.03
2.282e+001	2.424e-012	2.284e+001	0.09
2.915e+001	5.866e-013	2.915e+001	0.00
3.315e+001	1.795e-013	3.318e+001	0.09
5.801e+001	2.373e-011	5.803e+001	0.03
6.565e+001	3.028e-011	6.571e+001	0.09
6.873e+001	6.907e-014	6.875e+001	0.03
7.602e+001	1.549e-012	7.609e+001	0.09
9.949e+001	3.302e-013	9.953e+001	0.04

Example 4

Large building is presented in Fig. D3

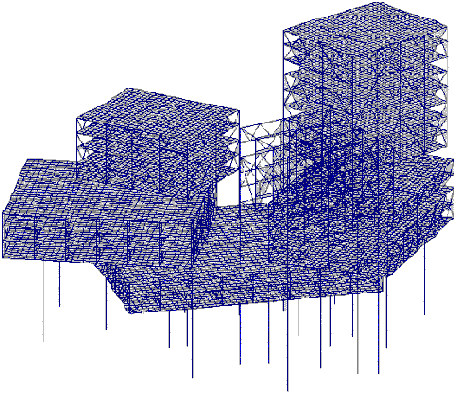
Fig. D3. Large building. Number of nodes: 26126, number of elements: 30272,

number of equations: 155920.

Linear static analysis (a single load case) and extraction of 10 eigenmodes are considered. The tolerance adopted for the iterative solver equals 1.0e-04. For the skyline solver Lanczos method is used. For sparse direct solver both Lanczos and BLSI methods are applied. Modified Lanczos method is used for iterative solver (multilevel method with 3 aggregation levels, 4 inner iterations, preconditioning ICCF). Mass matrix type: lumped with rotations is adopted.

Table D7. Computation time and disk space for several methods

Method	Disk space (MB)	Linear static (single rhs) (s)	Extraction of 10 eigenmodes (s)	Total time (s)
Skyline	5 702	136 065	65 052	203 878
AEBEIS	52	2 442	25 793	28 355
Sparse (Lanczos method)	773	10 253	24 500	35 762
Sparse NS (BLSI method)	773	10 253	11 534	22 604

Computations were performed on a PC-450 (128 MB RAM) computer.

Conclusions

Advanced methods: BLSI, Lanczos on the base of sparse direct solver and high-performance iterative solver AEBEIS with ICCF preconditioning are powerful tools for the solution of large-scale linear static and eigenvalue problems. They considerably reduce the computation time and disk storage requirements compared to a conventional skyline solver. Ritz-gradient method PCG_Ritz is a fast approach which allows one to estimate seismic behavior of the given structure. When a single aggregation level is accepted, the corresponding results, obtained by PCG_Ritz method, are close to the ones obtained by Lanczos or BLSI method.

References

E.L.Wilson. An eigensolution strategy for large systems. Computers&Structures, Vol.16, No. 1-4, pp.259-265, 1983.
Wilson. A new method of dynamic analysis for linear and nonlinear systems. Finite Elements in Analysis and Design, 1, 1985, 21-23, North-Holland.
E.L.Wilson, Three dimensional dynamic analysis of structures, Computers and Structures, Inc., Berkeley, California, USA, 1996.
R.W.Clough, J.Penzien. Dynamics of Structures. McGraw-Hill Book Comp., 1975, 634 p.
Fialko S. Yu. Investigations of the Initial Imperfections Influence to Natural Vibrations of Ribbed Conical Shells, Soviet Applied Mechanics, 1982, 18, N11, pp.118 - 122. (In Russian)
Fialko S. Yu. Nonsteady vibrations of ribbed conical shells under the influence of local loads, Soviet Applied Mechanics, 1987, v23, N6, p. 547-552.
Fialko S.Yu. High-performance aggregation element-by-element iterative solver for large-scale complex shell structure problems. Archives of Civil Engineering, XLV, 2, 1999. P.193-207.
Fialko S.Yu. High-performance aggregation element-by-element Ritz-gradient method for structure dynamic response analysis. CAMES (Computer assisted mechanics - engineering sciences), IV, 2000
Gambolati G., Pini G., Sartoretto F., An improved iterative optimization technique for the leftmost eigenpairs of large symmetric matrices, J. Comp. Phys., 74: 41 - 60, 1988.
Sartoretto F., Pini G., Gambolati G., Accelerated simultaneous iterations for large finite element eigenproblems, J. Comp. Phys., 81: 53 - 69, 1989.
Papadrakakis. A partial preconditioned conjugate gradient method for large eigenproblems, Comp. Meth. Appl. Mech. Eng., 62: 195 - 207, 1987.
Papadrakakis, Solving large -scale problems in mechanics, John Wiley & Sons Ltd., 1993.
S.Bitzarakis, M.Papadrakakis, A.Kotsopulos. Parallel solution techniques in computational structural mechanics. Comp. Methods Appl. Mech. Engrg. 1997, 148, p.75-104.
Hughes T.J.R., Ferencz M. Implicit solution of large-scale contact and impact problems employing an EBE preconditioned iterative solver, IMPACT 87 Int. Conference on Effects of Fast Transient Loading in the Context of Structural Mechanics, Lausanne, Switzerland, August 26-27, 1987.
Hughes T.J.R., R.M.Ferencz, and j.O.Hallquist. Large-scale vectorized implicit calculations in solid mechanics on a CRAY X-MP/48 utilizing EBE preconditioned conjugate gradients, Comput. Meths. Appl. Mech. Engrg., 61
Hughes Th. J. R. "The Finite Element Method. Linear Static and Dynamic. FEM Analysis."
Parlett B.N., 1980. "The Symmetric Eigenvalue Problem". Prentice-Hall, Inc., Englewood Cliffs, N.J. 07632.
Bulgakov, V.E., Belyi, M.E., Mathisen, K.M. Multilevel aggregation method for solving large-scale generalized eigenvalue problems in structural dynamics, Int. j. Numer. Methods Eng., 40: 453 - 471, 1997.
Bulgakov, V.E. Iterative aggregation technique for large-scale finite element analysis of mechanical systems, Comput. Struct, 52: N4, 829-840, 1994.
Bulgakov, V.E., G. Kuhn. High-performance multilevel iterative aggregation solver for large finite-element structural analysis problems, Int. j. Numer. Methods Eng., 38: 3529-3544, 1995.
Regulatory Guide
I.Ja.Amiro, V.A.Zarucky, V.N.Revutsky, Yu.V.Skosarenko, A.I.Telalov, S.Yu.Fialko. Oscillations of Ribbed Shells of Revolution, Kiev, Naukova Dumka, 1988, 169 p. (In Russian).
S.Yu.Filako. Natural Vibration Modes of Ribbed Conical Shells, Soviet Applied Mechanics, 1984, v20, N11, p. 1033-1037. (In English)