破断モデル

母材構成材料の塑性応答は、方程式1-8. によってまとめて定義されます。ただし、モデルは短繊維充填材料の完全な破損を識別する破断基準も使用する必要があります。Advanced Material Exchange では 3 つの破断基準を使用できます。

多項式応力

多項式応力法は、Advanced Material Exchange によって使用される既定の破断モデルです。多項式応力法では、母材の破断基準が母材の平均応力成分の二次関数であると仮定します。

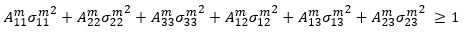
数量 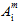(i = 11、22、33、12、13、23)は、母材破損基準の調整可能な係数です。これらは、0 度、90 度、45 度のデータ セットの引張テストから決定する必要があります。45 度の応力-ひずみデータがない場合は、90 度の曲線を使用し、応力のデータ点を 5% 上昇させます。破損係数の決定方法の詳細については、「材料特性」のトピックを参照してください。

破断の評価に使用される一連の破損係数は、モデルの各積分点における繊維配向テンソルの最大固有値によって異なります。最大固有値が 0.65 より大きい場合は、横等方性の挙動を仮定します。そのため、σ22m = σ33m、σ12m = σ13m となります。また、面外せん断応力成分 σ23m = σ12m = σ13m を仮定します。したがって、A22 = A33、A12 = A13 = A23 となります。

最大固有値が 0.65 以下の場合は、等方性の挙動を仮定します。そのため、σ11m = σ22m = σ33m、σ12m = σ13m = σ23m となります。したがって、A11 = A22 = A33、A12 = A13 = A23 となります。

MCT

MCT 法では、母材の破断基準が母材の平均応力成分の二次関数として表現されると仮定します。

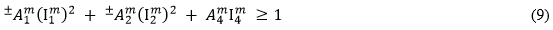
方程式 9 では、数量 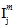(j = 1、2、4)は、母材の平均応力状態の横等方性不変量です。

数量 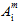(i = 1、2、4)は、母材破損基準の調整可能な係数です。これらは、0 度、90 度、45 度のデータ セットの引張テストから決定する必要があります。45 度の応力-ひずみデータがない場合は、90 度の曲線を使用し、応力のデータ点を 5% 上昇させます。破損係数の決定方法の詳細については、「材料特性」のトピックを参照してください。

最大有効応力

最大有効応力破壊モデルでは、有効応力式(重み付きフォン ミーゼス応力、式 6 を参照)の関数形式は、母材の塑性変形と母材の破壊の両方の予測に対する材料の方向依存性を定義するのに十分であると想定します。したがって、母材破断基準を決定するのに必要なことは、単に重み付け有効応力測定値の上限を確定することです(有効強度を Seff として示す)。この場合、母材破断基準は次のように表現されます。

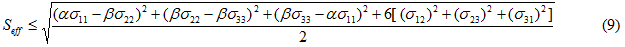
ここで、応力成分は母材構成材料の平均応力を表すものとします。

損傷の進展

母材破壊条件が満たされると(MCT か最大有効応力のどちらか)、破損した材料の構成関係にいくつかの変更が加えられます。

1. 母材の塑性変形を計算する必要がなくなるため、複合材料の応力とひずみを母材の応力とひずみに分解する必要はありません。
2. 構成関係とミクロ構造から複合材料の構成関係を構築する代わりに、均質化された複合材料の構成関係が直接使用されます(前述の説明を参照)。
3. 複合材料の剛性は、瞬時に複合材料の元の弾性剛性の数分の 1 にまで減少します。この剛性減少は、剛性マトリックスに劣化定数を乗算することによって実行されます。破壊条件が発生すると、複合材料の剛性はシミュレーションの期間中、減少した値のまま固定されることに注意してください。
4. 複合構成関係は、接線の形成(材料応答の塑性フェーズで使用)からセカントの形成に切り替えられます。破損した複合材料の剛性は固定されたままなので、問題の積分点はソリューションの非線形性には直接影響しません。