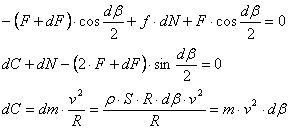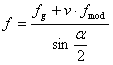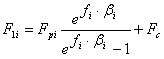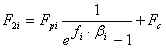一般的に用いる計算式
|
|
|
|
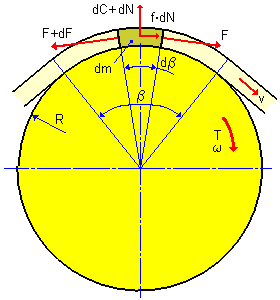
m はベルトの指定質量で、m = S ρ と定められます。 |
指定プーリの修正摩擦係数
|
|
|
|
|
f = f g + v f mod |
駆動プーリおよびベルトの基本計算式
伝達する動力
![]()
ベルト速度
![]()
ベルト柔軟頻度
![]()
有効張力
![]()
遠心力
Fc = z m v 2
ベルト スパンの張力
次の計算式によって、アプリケーションはまず、負荷を伝動するために最大ベルト取り付け張力が必要となる可能性が最も高いプーリを特定します。次に初期のベルト取り付け張力に関し、すべてのプーリで各スパンのベルト張力が調整されます。
|
|
|
|
F 1i - F p P xi - F 2i = 0 |
|
|
|
|
|
|
最も可能性の高いプーリの基準は、最大張り側張力
F 1max = max (F 1i )
ベルト駆動が最大荷重に達していない場合、ベルト スパン(ベルトごと)の合計最大張力は、次のように求められます。
![]()
ここで、式 "k 1 F 1max " は、ベルト伝動におけるすべてのベルトを考慮した、ベルト スパンの実際の最大張力です。この方法では、個々のスパンにおける対応する張力がすべて、次の条件を満たすように再計算されます。
F 1i - F P P xi - F 2i = 0
ベルト駆動が最大荷重に達していない場合、各プーリの結果軸荷重は次の通りです。
![]()
![]()
初期のベルト取り付け張力および静的張力
必要となる初期のベルト取り付け張力(ベルトごと)は、張力係数を調整した後、次のように求めます。
![]()
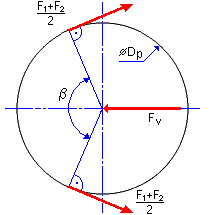
静的張力 F v はプーリごとに求めます。ベルト スパンの中心線に沿って実行される張力は次のように計算されます。
|
|
|
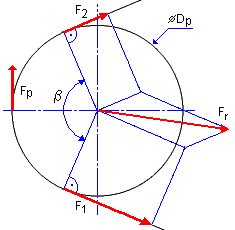
使用される変数の意味:
| F | 接線力[N] |
| β | 接触弧[度] |
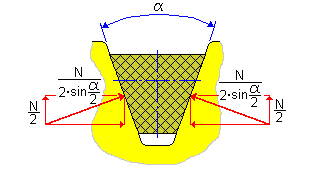
| α | ウェッジ角度[度] |
| C | 遠心力[N] |
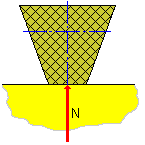
| N | 垂直力[N] |
| m | 指定ベルト質量[Kg/m] |
| v | ベルト速度[m/秒] |
| R | プーリ半径[m] |
| S | ベルト断面領域[m 2 ] |
| T | 指定のプーリに作用するトルク[Nm] |
| D p | プーリ ピッチ円直径[m] |
| k | プーリの数[-] |
| P | 伝達する動力[W] |
| v | ベルト速度[m/秒] |
| F c | 遠心力[N] |
| F 1 | 指定プーリの入力側ベルト スパンでの張力[-] |
| F 2 | 指定プーリの出力側ベルト スパンでの張力[-] |
| f | 指定プーリの修正摩擦係数[-] |
| P x | 指定のプーリの動力比[-] |
| f g | 指定プーリ材料およびベルトの摩擦係数[-] |
|
f mod |
摩擦修正の速度係数[s/m] |
| Z | ベルト数[-] |
| ρ | ベルト密度[kg/m3] |
| F t | ベルトの初期取り付け張力[N] |
| F v | 指定プーリの静的張力[N] |
| k 1 | ベルト張力係数[-] |