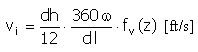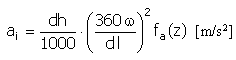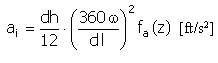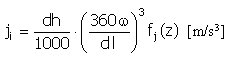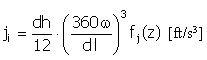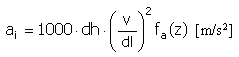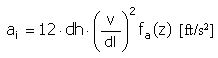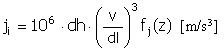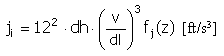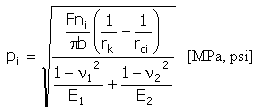カムの計算式

入力データ:

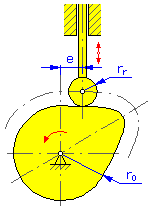
• 基礎円半径 r ₀ (円板カムと円筒カム)
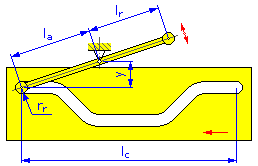
• 回転長 l _c (板カム)
• カム幅 b _c
• ローラの半径 r _r
• ローラ幅 b _r (フォロア形状の円柱の場合)
• 偏心度 e (直動フォロア用の円板カム)
• 偏心角 α (直動フォロア用の板カムと円筒カム)
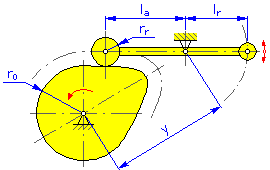
• 回転軸距離 y (スウィング アーム用の円板カムと板カム)
• アームの長さ l _a (スウィング アーム用の円板カムと板カム)
• 従動アーム l _r (スウィング アーム用の円板カムと板カム)
• スピード ω (円板カムと円筒カム)
• 速度 v (板カム)
• ローラに掛かる力 F
• 慣性質量 m
• ばね等級 c
• 許容圧力 p _A1
• カムの材料の弾性係数 E ₁
• カムの材料のポアソン比 μ ₁
• 許容圧力 p _A2
• フォロワの材料の弾性係数 E ₂
• フォロワの材料のポアソン比 μ ₂

円板カム
板カム
円筒ｶﾑ
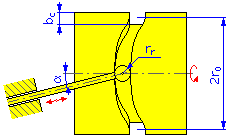外径 = 2r 0 + b c
内径 = 2r 0 - b

カムのセグメント

• モーション関数 f _y (z) [ul]
• リバース比 k _r (モーション放物線および直線部を持つ放物線の場合のみ)
• 直線部 k _l (直線部を持つモーション放物線の場合のみ)
• 回転の開始位置 l ₀ [°、mm、インチ]
• 回転の終了位置 l [°、mm、インチ]
• セグメントのモーションの長さ dl = l - l ₀ [°、mm、インチ]
• 開始位置のリフト量 h ₀ [mm、インチ]
• 終了位置のリフト量 h _max [mm、インチ]
• セグメント リフト d _h = h _max - h ₀ [mm、in]

リフトの従属

円板カムと円筒カム

カム回転角 ϕ _i [°]

セグメント内の実際の相対位置: z _i = (ϕ _i - L ₀ ) / dL (範囲 0 ～ 1)

変位	y i = dh f y (z) [mm, in]
[速度]
加速度
パルス

板カム

カムのモーション位置 L _i [mm、インチ]

セグメント内の実際の相対位置: z _i = (l _i - l ₀ ) / dL (範囲 0 ～ 1)

変位	y i = dh f y (z) [mm, in]
速度
加速度
パルス

モーション関数

サイクロイド(拡張正弦)

このモーションには優れた加速度特性があります。結果として生じる騒音、振動、磨耗が低レベルであるため、高速カムによく使用されます。

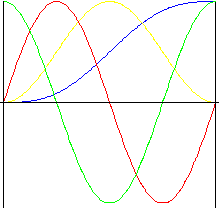
	変位
	速度
	加速度
	パルス

変位	f y (z) = z - 0.5/π sin(2πz)
速度	f v (z) = 1 - cos(2πz)
加速度	f a (z) = 2π sin(2πz)
パルス	f j (z) = 4π 2 cos(2πz)

緩和曲線(正弦)

ストローク時に速度と加速度が滑らかであることが、この曲線に固有の利点です。ただし、モーションの最初または最後で加速度に瞬間的な変化が発生すると、振動、騒音、および磨耗の原因となる可能性があります。

	変位
	速度
	加速度
	パルス

変位	f y (z) = 0.5 (1 - cos πz))
速度	f v (z) = 0.5 π sin (πz)
加速度	f a (z) = 0.5 π 2 cos(πz)
パルス	f j (z) = -0.5π 3 sin(πz)

線形

モーションの最初と最後に大きな衝撃のある単純なモーション。非常に粗雑なデバイスを除き、ほとんど使用されません。モーションの最初と最後が変更されたもの、つまり、直線部を持つ放物線を使用することをお勧めします。

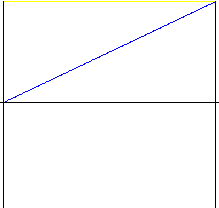
	変位
	速度

変位	f y (z) = z
速度	f v (z) = 1
加速度	f a (z) = 0
	注: z = 0 および z = 1 の場合、固有値は無限値ですが、無限値であると計算できないため、ゼロ値を使用します。
パルス	f j (z) = 0
	注: z = 0 および z = 1 の場合、固有値は無限値ですが、無限値であると計算が行えないため、ゼロ値を使用します。

放物線(2 ^nd 次の多項式)

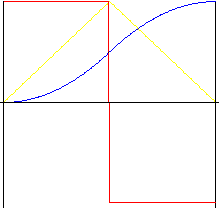
加速度が可能な限り最小のモーション。ただし、モーションの最初、中間、または最後で加速度に突然の変化が発生すると、衝撃が生じます。反転比によりモーションの中間で「ストレッチ」が可能になり、加速度および減速度の変更が可能になります。

対称(反転比 k _r = 0.5)

	変位
	速度
	加速度

	z = 0 ～ 0.5 の場合:
		変位	fy(z) = 2z 2
		速度	fv(z) = 4z
		加速度	fa (z) = 4
		パルス	fa(z) = 0
	z = 0.5 ～ 1 の場合:
		変位	fy(z) = 1 - 2(1 - z) 2
		速度	fv(z) = 4 (1 - z)
		加速度	fa (z) = -4
		パルス	fj(z) = 0
			注: z = 0 および z = 1 の場合、固有値は無限値ですが、無限値であると計算が行えないため、ゼロ値を使用します。

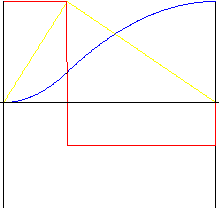
非対称

k _r - リバース比(範囲 0.01 ～ 0.99)

	変位
	速度
	加速度

	z = 0 ～ k r の場合:
		変位	f y (z) = z 2 / k r
		速度	f v (z) = 2z / k r
		加速度	f a (z) = 2 / k r
		パルス	f j (z) = 0
	z = k r ～ 1 の場合:
		変位	f y (z) = 1 – (1 – z) 2 / (1 – k r )
		速度	f v (z) = 2 (1 – z) / (1 – k r )
		加速度	f a (z) = -2 / (1 - k r )
		パルス	f j (z) = 0
			注: z = 0 および z = 1 の場合、固有値は無限値ですが、無限値であると計算が行えないため、ゼロ値を使用します。

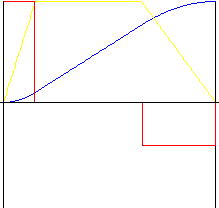
直線部を持つ放物線

直線的モーションよりも満足できる加速度と減速度が提供されます。反転比によりモーションの中間で「ストレッチ」が可能になり、加速度および減速度の変更が可能になります。直線部の比により、直線的モーション部の相対サイズを設定できます。

	速度
	加速度
	パルス

k _r - リバース比(範囲 0.01 ～ 0.99)

k _l - 直線部の比(範囲 0 ～ 0.99)

k _z = 1 + k _l / (1 - k _l )

k _h = (1 - k _l ) / (1 + k _l )

	z = 0 ~ k r / k z の場合:
		変位	f y (z) = k h z 2 k z 2 / k r
		速度	f v (z) = 2 k h z k z 2 / k r
		加速度	f a (z) = 2 k h k z 2 / k r
		パルス	f j (z) = 0
	z = k r / k z ～ r / k z + k l の場合:
		変位	f y (z) = (z - 0.5 k r / k z ) 2 / (1 + k l )
		速度	f v (z) = 2 / (1 + k l )
		加速度	f a (z) = 0
		パルス	f j (z) = 0
	z = k r / k z + k l ～ 1 の場合:
		変位	f y (z) = 1 - k h (1 - z) 2 k z 2 / (1 - k r )
		速度	f v (z) = 2 k h (1 - z) k z 2 / (1 - k r )
		加速度	f a (z) = -2 k h k z 2 / (1 - k r )
		パルス	f j (z) = 0

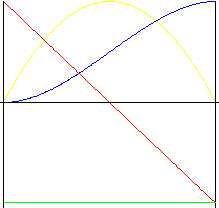
3 次の多項式 ^rd (3 次放物線)

放物線モーションより衝撃が小さいモーション。

	変位
	速度
	加速度
	パルス

変位	f y (z) = (3 -2z) z 2
速度	f v (z) = (6 - 6z) z
加速度	f a (z) = 6 - 12z
パルス	f j (z) = -12

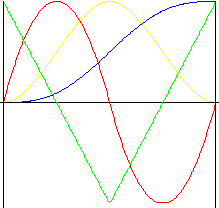
4 次の多項式 ^th

3 ^rd 次の多項式のモーションより衝撃が小さいモーション。

	変位
	速度
	加速度
	パルス

z = 0 ～ 0.5 の場合
	変位	f y (z) = (1 - z) 8z 3
	速度	f v (z) = (24 - 32z) z 2
	加速度	f a (z) = (48 - 96z) z
	パルス	f j (z) = 48 - 192z
z = 0.5 ～ 1 の場合
	変位	f y (z) = 1 - 8z (1 - z) 3
	速度	f v (z) = (32z - 8) (1 - z) 2
	加速度	f a (z) = (48 - 96z) (1 - z)
	パルス	f j (z) = 194z - 144

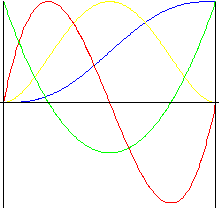
5 次の多項式 ^th

3 ^rd 次の多項式のモーションより衝撃が小さいモーション。

	変位
	速度
	加速度
	パルス

変位	f y (z) = (6z 2 - 15z + 10) z 3
速度	f v (z) = (z 2 - 2z + 1) 30z 2
加速度	f a (z) = (2z 2 - 3z + 1) 60z
パルス	f j (z) = (6z 2 - 6z + 1) 60

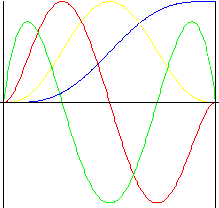
7 次の多項式 ^th

パルスを含むすべての計算式で滑らかです。

	変位
	速度
	加速度
	パルス

変位	f y (z) = (-20z 3 + 70z 2 - 84z + 35) z 4
速度	f v (z) = (-z 3 + 3z 2 - 3z + 1) 140z 3
加速度	f a (z) = (-2z 3 + 5z 2 - 4z + 1) 420z 2
パルス	f j (z) = (-5z 3 + 10z 2 - 6z + 1) 840z

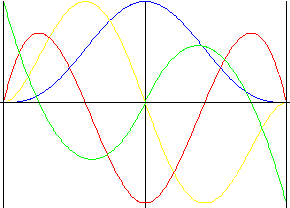
非対称の 5 次の多項式 ^th

5 次の多項式に似ていますが、変位反転が強制的に行なわれます。

注: パーツ 1 とパーツ 2 の組み合わせを必要とします。

	変位
	速度
	加速度
	パルス

パーツ 1
	変位	f y (z) = 1 - (8 (1 - z) 3 - 15 (1 - z) 2 + 10) (1 - z) 2 / 3
	速度	f v (z) = (2 (1 - z) 3 - 3 (1 - z) 2 + 1) (1 - z) 20 / 3
	加速度	f a (z) = -(8 (1 - z) 3 - 9 (1 - z) 2 + 1) 20 / 3
	パルス	f j (z) = (4 (1 - z) 2 - 3 (1 - z)) 40

パーツ 2
	変位	f y (z) = (8z 3 - 15z 2 + 10) z 2 / 3
	速度	f v (z) = (2z 3 - 3z 2 + 1) z 20/3
	加速度	f a (z) = (8z 3 - 9z 2 + 1) 20/3
	パルス	f j (z) = (4z 2 - 3z) 40

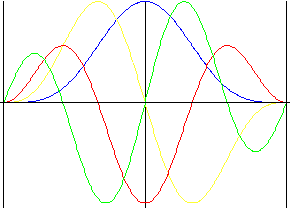
調和平均

変位反転が強制的に行なわれるパルスを含むすべての計算式で滑らかです。

注: パーツ 1 とパーツ 2 の組み合わせを必要とします。

パーツ 1
	変位	f y (z) = cos(0.5π (1 - z)) 4
	速度	f v (z) = π (0.5 sin(πz) - 0.25 sin(2πz))
	加速度	f a (z) = 0.5 π 2 (cos(πz) - cos(2πz))
	パルス	f j (z) = π 3 (-0.5 sin(πz) + sin(2πz))

パーツ 2
	変位	f y (z) = 1 - cos(0.5π z) 4
	速度	f v (z) = π (0.5 sin(πz) + 0.25 sin(2πz))
	加速度	f a (z) = 0.5 π 2 (cos(πz) + cos(2πz))
	パルス	f j (z) = -π 3 (0.5 sin(πz) + sin(2πz))

最大相対値の比較

[モーション]	速度	加速度	パルス
サイクロイド(拡張正弦)	2	6.28	39.5
緩和曲線(正弦)	1.57	4.93	15.5
線形	1	∞	∞
放物線(2 nd 次の多項式)	2	4	∞
3 rd 次の多項式	1.5	6	12
4 th 次の多項式	2	6	48
5 th 次の多項式	1.88	5.77	60
7 th 次の多項式	2.19	7.51	52.5
非対称の 5 th 次の多項式	1.73	6.67	40
調和平均	2.04	9.87	42.4

その他の従属

ローラに掛かる力

F i = F + m a i + c y i [N, lb]

垂直力

Fn i = F i / cos (γ i ) [N、lb]

モーメント

T i = F i r i tan (γ i ) [Nmm、lb in]

指定(ヘルツ)圧力

	b = min (b v, b k )