メートル単位でのねじりばねの計算

一般的な計算式

コイルの外径

D₁ = D + d [mm]

ここで

	D	平均ばね直径 [mm]
	d	線径[mm]

コイルの内径

D₂ = D - d [mm]

ここで

	D	平均ばね直径 [mm]
	d	線径[mm]

あらかじめ荷重を加えたばねのトルク

ここで

	F₁	あらかじめ荷重を加えたばねの作動力[N]
	R₁	作動力アーム [mm]

完全に荷重がかかったばねのトルク

ここで

	F₈	(完全に荷重がかかったばねの)作動力[N]
	R₁	作動力アーム [mm]

ばね指数

c = D/d [-]

ここで

	D	平均ばね直径 [mm]
	d	線径[mm]

作動ストロークの角度

ϕ _h = ϕ₈ - ϕ₁ [°]

ここで

	ϕ ₈	完全に荷重がかかった状態での作動アームのたわみ角度[°]
	ϕ ₁	あらかじめ荷重を加えた状態での作動アームのたわみ角度[°]

作動アームの最小たわみ角度

ここで

	M₁	あらかじめ荷重を加えたばねのトルク[Nm]
	k	ねじりばね比[Nm/°]
	ϕ _h	作動ストロークの角度[°]
	M₈	完全に荷重がかかったばねのトルク [Nm]

作動アームの最大たわみ角度

ここで

	M₁	あらかじめ荷重を加えたばねのトルク[Nm]
	k	ねじりばね比[Nm/°]
	ϕ _h	作動ストロークの角度[°]
	M₈	完全に荷重がかかったばねのトルク [Nm]

応力集中係数

ここで

	i	ばね指数[-]
	i = D/d [-]	有効コイルの曲げ応力の計算用
		アームの曲げ応力の計算用
	r	アームの曲げ半径(内側) [mm]
	d	線径[mm]

一般的なばねの材料の応力

ここで

	M	一般的な、ばねのトルク [Nm]
	K_f	応力集中係数 [-]
	d	線径[mm]

ばねの有効巻数

ここで

	ϕ	一般的な、作動アームのたわみ角度[°]
	E	弾性係数[psi]
	d	線径[mm]
	M	一般的な、ばねのトルク[Nm]
	R₁	作動力アーム [mm]
	R₂	支持力アーム[mm]
	D	平均ばね直径[mm]

ばねの設計計算

ばねの設計で、線径、巻数、および曲げフックアームの曲げ半径は、特定の荷重、材料、および取付寸法に適合するように設計されます。推奨される線径に適したばねを設計してください。コイル間のクリアランス、つまり自由状態のばねスレッドの t ピッチは、0.3 D ≤ t ≤ 0.5 D [mm]の範囲に収まるようにする必要があります。

ばねの設計は強度条件 (σ₈≤ u_ssA)および(σ_8r≤ u_sσ_A と、一部のばねジオメトリ寸法の推奨範囲を基準にします。

L_Z≤ 10 D かつ L_Z≤ 31.5 in かつ 4 ≤ D/d ≤ X かつ n≥ 1.5 かつ 1.2 d ≤ t < D かつ r ≥ d

ここで

密巻きコイルばね X = 16
緩巻きコイルばね X = 10

ばねの寸法は、アームの特定の形状と長さに応じた、実現可能な幾何学的な解決方法に合わせます。仕様で指定されている場合、寸法は取付の限界寸法に適合していなければなりません。限界寸法は、最大許容ハウジング直径および長さ、または最大許容棒直径です。

指定された最大荷重、材料、およびばねの取付寸法

最初に、計算の入力値がチェックされます。

次に、指定された最大荷重および取付寸法に対する最小荷重を計算します。

ここで

	M₁	あらかじめ荷重を加えたばねのトルク[Nm]
	M₈	完全に荷重がかかったばねのトルク [Nm]
	ϕ ₁	あらかじめ荷重を加えた状態での作動アームのたわみ角度[°]
	ϕ ₈	完全に荷重がかかった状態での作動アームのたわみ角度[°]

これが完了したら、ばね径を計算した後に強度とジオメトリックの両条件を満たすように、線径と巻数を設計します。ばね径値が仕様で限定されている場合、ばねの設計はこれに準拠する必要があります。限定されていない場合、ばね径限度は、最小および最大許容線径の幾何条件によって決まります。

フックアーム付きのばねの場合、曲げアームの最適な半径が設計されます。

指定された強さと幾何条件に適合するすべてのばね線径が計算され、最小から始まって最大の方に向かいます。次に、最適な巻数に必要なすべての条件に適合しているかどうかをテストします。条件をすべて満たす場合、他の適合したばね線径に関係なく、設計は選択された値で終了し、ばねは最小線径、最小巻数、最小ばね直径で設計されます。

指定された荷重、材料、および作動たわみ角度

最初に、計算の入力値がチェックされます。

指定された荷重と作動たわみ角度に対して、作動アームのたわみ角度が計算されます。

作動アームの最小たわみ

作動アームの最大たわみ

ここで

	M₁	あらかじめ荷重を加えたばねのトルク[Nm]
	M₈	完全に荷重がかかったばねのトルク [Nm]
	ϕ ₁	あらかじめ荷重を加えた状態での作動アームのたわみ角度[°]
	ϕ ₈	完全に荷重がかかった状態での作動アームのたわみ角度[°]
	ϕ _h	作動ストロークの角度[°]

次に、ばね径を計算した後に強度とジオメトリックの両条件を満たすように、線径と巻数を設計します。ばね径値が仕様で限定されている場合、ばねの設計はこれの条件に準拠する必要があります。限定されていない場合、ばね径限度は、最小および最大許容線径の幾何条件によって決まります。

フックアーム付きのばねの場合、曲げアームの最適な半径が設計されます。

指定された強さと幾何条件に適合するすべてのばね線径が考慮され、最小線径から始まって最大の方に向かいます。次に、最適な巻数に必要な条件に適合しているかどうかをテストします。条件をすべて満たす場合、他の適合したばね線径に関係なく、設計は選択された値で終了し、ばねは最小線径、最小巻数、最小ばね直径で設計されます。

指定された最大荷重、材料、およびばね径

最初に、計算の入力値がチェックされます。

次に、強さと幾何条件に合うように線径、コイル数、および取付寸法を設計します。作動たわみ角度が仕様で限定されている場合、ばねの設計はこれの条件に従う必要があります。限定されていない場合、取付寸法の制限は、指定されたばね径および最小または最大許容線径の幾何条件によって決まります。

フックアーム付きのばねの場合、曲げアームの最適な半径が計算されます。

指定された強度とジオメトリックの両条件を持つすべてのばね線径が考慮され、それぞれ最小から最大まで線径を増やして計算し設計されます。次に、巻数に必要なすべての条件に適合しているかどうかをテストします。条件をすべて満たす場合、他の適合したばね線径に関係なく、設計は選択された値で終了し、ばねは最小線径、最小巻数、最小ばね直径で設計されます。

指定された最大荷重、材料、ばね径、および作動たわみ角度

最初に、計算の入力値がチェックされます。

次に、前述の強度とジオメトリックの両条件に合うように線径、巻数、および作動アームのたわみ角度を最適化します。プログラムは、作動アームの最小たわみ角度 ϕ₁ が約 2°になるような、作動アーム ϕ₈ の最大たわみ角度の最小値を探します。

フックアーム付きのばねの場合、曲げアームの最適な半径が計算されます。

最後に、指定された最大荷重と設計した作動アームのたわみ角度に対して、最小ばね荷重を計算します。

ここで

	M₁	あらかじめ荷重を加えたばねのトルク[Nm]
	M₈	完全に荷重がかかったばねのトルク [Nm]
	ϕ ₁	あらかじめ荷重を加えた状態での作動アームのたわみ角度[°]
	ϕ ₈	完全に荷重がかかった状態での作動アームのたわみ角度[°]

指定された強度とジオメトリックの両条件を持つすべてのばね線径が考慮され、それぞれ最小から最大までワイヤ直径を増やして計算されます。次に、巻数に必要なすべての条件に適合しているかどうかをテストします。条件をすべて満たす場合、他の適合したばね線径に関係なく、設計は選択された値で終了し、ばねは最小線径、最小巻数、最小ばね直径で設計されます。

ばねの計算チェック

指定された荷重、材料、ばねの寸法について、取付寸法の対応値を計算します。まず入力データをチェックして計算し、次の数式から取付寸法が計算されます。

作動アームの最小たわみ角度

ここで

	M₁	あらかじめ荷重を加えたばねのトルク[Nm]
	D	平均ばね直径 [mm]
	n	有効巻数[-]
	R₁	作動力アーム [mm]
	R₂	支持力アーム [mm]
	E	引張弾性係数[MPa]
	d	線径[mm]

作動アームの最大たわみ角度

ここで

	M₈	完全に荷重がかかったばねのトルク [Nm]
	D	平均ばね直径 [mm]
	n	有効巻数[-]
	R₁	作動力アーム [mm]
	R₂	支持力アーム [mm]
	E	引張弾性係数[MPa]
	d	線径[mm]

作動ストロークの角度

ϕ _h = ϕ₈ - ϕ₁ [°]

ここで

M₈	完全に荷重がかかったばねのトルク [Nm]
ϕ ₈	完全に荷重がかかった状態での作動アームのたわみ角度[°]

作動力の計算

指定された材料、取付寸法、ばねの寸法について、作動状態のばねによって加えられた力を計算します。入力データをチェックして計算し、次の数式から作動力が計算されます。

最小作動荷重

ここで

	M₁	あらかじめ荷重を加えたばねのトルク[Nm]
	D	平均ばね直径 [mm]
	n	有効巻数[-]
	R₁	作動力アーム [mm]
	R₂	支持力アーム [mm]
	E	引張弾性係数[MPa]
	d	線径[mm]
	ϕ ₁	あらかじめ荷重を加えた状態での作動アームのたわみ角度[°]

最大作動荷重

ここで

	M₈	完全に荷重がかかったばねのトルク [Nm]
	D	平均ばね直径 [mm]
	n	有効巻数[-]
	R₁	作動力アーム [mm]
	R₂	支持力アーム [mm]
	E	引張弾性係数[MPa]
	d	線径[mm]
	ϕ ₈	完全に荷重がかかった状態での作動アームのたわみ角度[°]

ばねの出力パラメータの計算

すべての種類のばねの計算に共通です。次の順序で計算します。

ねじりばね比

緩巻きばねの巻きクリアランス

a = t - d [mm]

緩巻きばねの巻き部長さ

密巻きばね用
	L₀ = (1.05 n + 1) d [mm]
緩巻きばね用
	L₀ = t n + d [mm]

最小作動荷重に対する有効コイルでのばねの材料の曲げ応力

ここで、応力集中係数 K_f は i = D/d で計算されます。

最小作動荷重に対する曲げアームでのばねの材料の曲げ応力

ここで、応力集中係数 K_f は i = 2r/d + 1 で計算されます。

完全に荷重がかかった場合の、有効コイルでのばねの材料の曲げ応力

ここで、応力集中係数 K_f は i = D/d で計算されます。

完全に荷重がかかった場合の、曲げアームでのばねの材料の曲げ応力

ここで、応力集中係数 K_f は i = 2r/d + 1 で計算されます。

密巻きばねの完全に荷重がかかっている状態で、荷重がばねを取り巻いている場合の、巻き部長さ

完全に荷重がかかった状態で、荷重がばねを取り巻いている場合の、ばねの外径

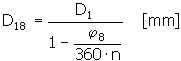
完全に荷重がかかった状態で、荷重がばねを取り巻いている場合の、ばねの内径

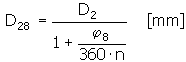
作動アームのたわみ角度の限界テスト

ばねの変形エネルギー

ワイヤ長さ

l = 3.2 D n + l_R [mm]
ここで l_R はアーム長さ、一方
	ここで l_R はアーム長さ、一方
		直線ねじりアームの長さ

		フックアームの長さ

ばね質量

ばね荷重のチェック

(σ₈≤ u_sσ_A)かつ(σ_8r≤ u_sσ_A)

使用される変数の意味:

a	自由状態の有効コイル間のスペース[mm]
d	線径[mm]
D	平均ばね直径 [mm]
D₁	ばねの外径 [mm]
D₂	ばねの内径 [mm]
E	弾性係数 [psi]
F	一般的な、ばねから伝わる作動力(作動力アーム R₁ に伝わる力) [N]
i	ばね指数 [-]
K_F	応力集中係数 [-]
kϕ	ねじりばね比[Nm/°]
r₁	作動アームにおける曲げ半径 [mm]
r₂	支持アームにおける曲げ半径 [mm]
R₁	作動力アーム [mm]
R₂₁	支持力アーム [mm]
l	ワイヤの長さ [mm]
L₀	一般的な、緩んだ状態での巻き部長さ[mm]
m	ばね質量[N]
M	一般的な、ばねのトルク [Nm]
n	有効巻数[-]
t	緩んだ状態でのコイル間のピッチ [mm]
u_s	材料の稼働係数
ρ	ばねの材料の密度[lb/ft3]
ϕ	一般的な、作動アームのたわみ角度[°]
σ	一般的なばねの材料の曲げ応力 [psi]
σ _A	ばね材料の許容曲げ応力 [psi]
M₁	あらかじめ荷重を加えたばねのトルク[Nm]
M₈	完全に荷重がかかったばねのトルク [Nm]
ϕ ₈	完全に荷重がかかった状態での作動アームのたわみ角度[°]
ϕ ₁	あらかじめ荷重を加えた状態での作動アームのたわみ角度[°]
ϕ ₈	完全に荷重がかかった状態での作動アームのたわみ角度[°]
ϕ _h	完全に荷重がかかった状態での作動アームのたわみ角度[°]