超弾性

この材料タイプは陽解法解析ではサポートされていません。アイソパラメトリック ソリッド要素のゴム状の材料(エラストマー)の完全に非線形(大きなひずみと大きな回転)超弾性解析で使用する材料特性を定義します。

• 一般化された Mooney-Rivlin ひずみエネルギーは、次のように表すことができます。

  

  ここで、 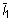および はそれぞれ 1 番目と 2 番目の変形ひずみ不変量で、J = det F は変形勾配の既知数です。そして、小さなひずみにおいては 2D1 = K および 2(A10 + A01) = G であり、ここで K は体積弾性率です。モデルは、NA = 1 の場合は Mooney-Rivlin 材料に、NA = 1 で A01 = 0.0 の場合は Neo-Hookean 材料になります。Neo-Hookean 材料または Mooney-Rivlin 材料に対して、継続エントリは必要ありません。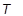 は現在の温度、 は初期温度です。

• 一般化された Ogden ひずみエネルギーは、次のように表すことができます。

  

  ここで、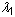、 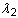および 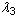は主伸張で、J = det F は変形勾配の既知数です。小さなひずみにおいては 2D1 = K であり、ここで K は体積弾性率です。 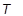は現在の温度、 は初期温度です。

  D1 の既定は 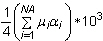です。D2 から D4 までの既定はゼロです。

• 超弾性材料は完全な非圧縮性、またはほぼ非圧縮性の挙動を示します。現在、完全な非圧縮性は使用できませんが、ほぼ非圧縮性の挙動は大きな D1 値を使用してシミュレーションできます。

[超弾性]を[タイプ]ドロップダウンから選択すると、次の材料セクションが使用できるようになります: [超弾性]、[実験データ関数]、および[Mullins 係数]。

• 超弾性

  

  

  

  

  

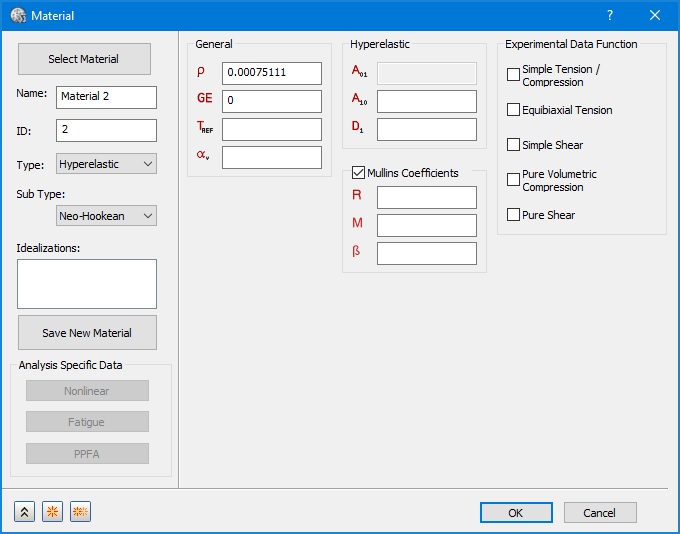
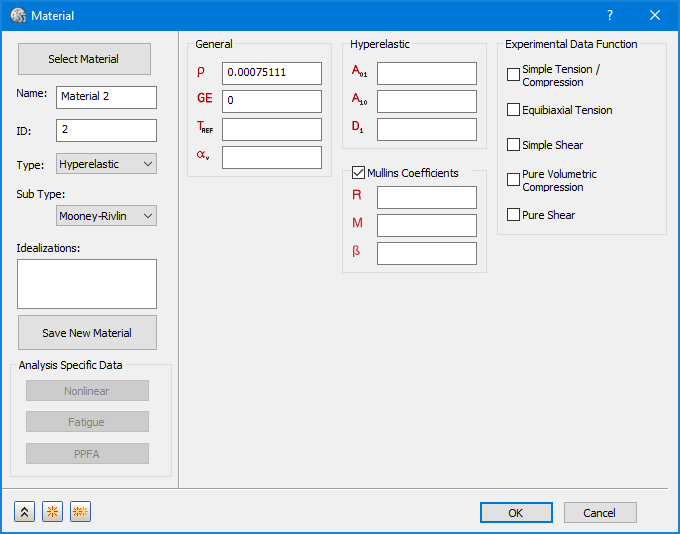
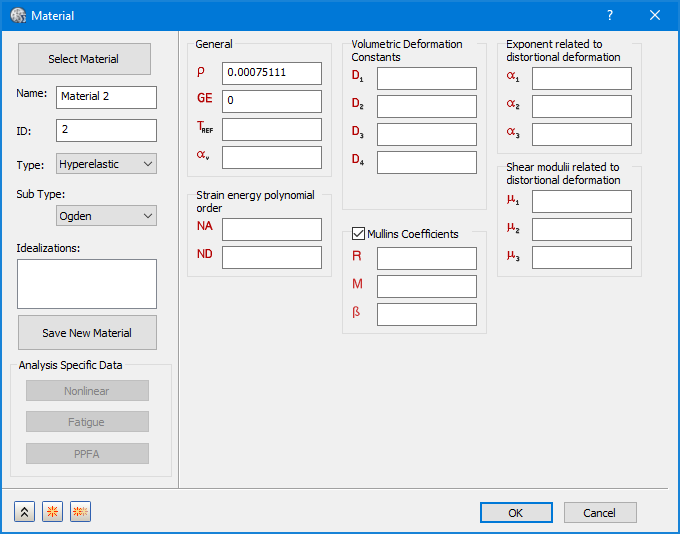
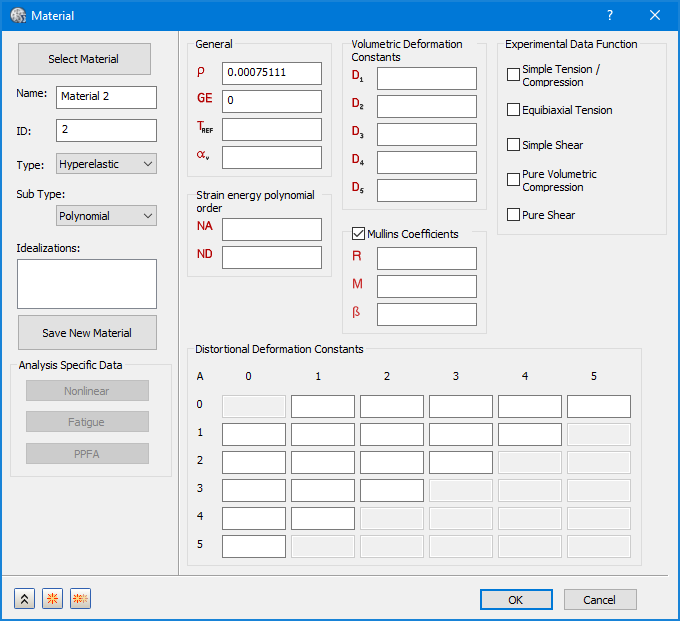
  • 上記のイメージに示すように、[サブ タイプ]に対して、Neo-Hookean、Mooney-Rivlin、オグデン、Yeoh、Polynomialから選択することができます。各タイプには、定義する材料定数セットがあります。
  • すべての構造要素に対して自動的に質量を計算するために、質量密度、RHO が使用されます。
  • 減衰係数 GE を取得するには、臨界減衰比 C/C0 を 2.0 で乗算します。材料構造減衰に対して優位周波数が定義されていない場合(「減衰」セクションを参照)、過渡応答解析では GE は無視されます。
  • 線形解析の熱荷重計算では、TREF は参照温度としてのみ使用されます。初期温度荷重が指定されている場合、TREF は無視されます。
  • 熱膨張係数、質量密度、材料減衰係数、および材料の参照材料を定義できます。
• 実験データ関数
  • Aij および DI は、フィット実験データの最小二乗から取得されます。4 つの実験(単純引張圧縮、等二軸引張、単純せん断、純せん断、純体積圧縮)の 1 つまたは複数を使用して Aij を取得します。Di は純体積圧縮データ(TABD)から取得できます。TAB1 から TAB4 まですべてが空白の場合、Aij はユーザによって指定される必要があります。テーブルのいずれかで指定されたパラメータの予測は、手動入力のパラメータより優先されます。
  • ND = 1 およびゼロ以外の D1 値が入力された場合、または純体積圧縮の実験データから取得された場合、材料定数 Aij のパラメータの予測は、単純引張/圧縮、等二軸引張、および一般的な二軸変形の場合に圧縮性を考慮します。それ以外の場合は、材料定数の予測では、完全な非圧縮性を仮定します。

    

    • テーブル アイコン: 物理テストで取得した実験データ関数を定義できます。[単純引張/圧縮]、[等二軸引張]、[単純せん断]、[純せん断]、[純体積圧縮]のテーブルを定義できます。
    • [単純引張/圧縮]: 材料定数 Aij の予測に使用するデータです。テーブル内の xi 値は伸長比 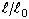で、yi 値は工学応力値 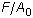である必要があります。応力は圧縮に対して負の値で、引張りに対して正の値となります。この規則が順守されない場合、解析の収束に失敗する場合があります。
    • [等二軸引張]: 材料定数 Aij の予測に使用するデータです。テーブル内の xi 値は伸長比 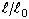である必要があります。yi 値は工学応力値 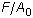である必要があります。 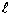は現在の長さ、F は現在の力、 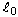は初期長さ、 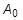は断面積です。球状膜の圧力の場合、工学応力は で求められ、ここで P は圧力の現在の値、 と 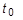は初期半径および厚さです。
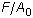    • [単純せん断]: 材料定数 Aij の予測に使用するデータです。テーブル内の xi 値はせん断接線 で、yi 値は工学応力値 である必要があります。
    • [純せん断]: 材料定数 Aij の予測に使用するデータです。テーブル内の xi 値と yi 値は伸長比 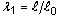で、公称応力値 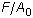である必要があります。 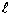は現在の長さ、F は現在の力、 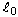と 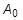は初期長さおよび断面積で、それぞれ 1-方向にあります。
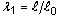    • [純体積圧縮]: 材料定数 Di の予測に使用するデータです。テーブル内の xi 値は体積比 の値である必要があり、ここで は 3 方向すべての伸長比で、yi 値は圧力の値である必要があり、圧縮において正の値であると仮定します。
• Mullins 係数(陽解法解析のみ)
  
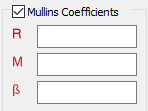
  • 超弾性材料の Mullins 効果を指定します。このチェックボックスは、陽解法解析を実行する場合にのみオンにする必要があります。
  • R、M、β は Mullins 係数です。